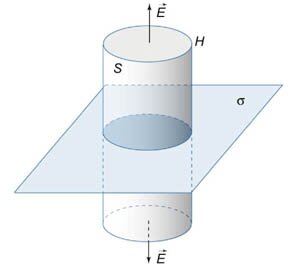
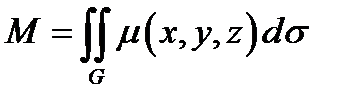Пример 12.1.Найдём массу части плоскости , ограниченной координатными плоскостями, если плотность в каждой точке .

Решение. Построим заданную часть плоскости ( см. рис. 12.1). .

Поверхность G однозначно проецируется на координатную плоскость XOY, поэтому для вычисления массы (12.5) применим формулу (12.1).

Рисунок 5.1

где , .

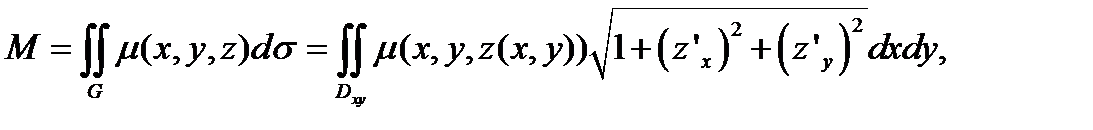
Подставляем всё в подынтегральное выражение и вычисляем интеграл.

.

Ответ: .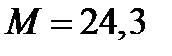

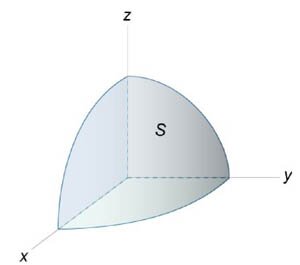
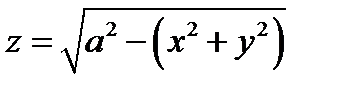
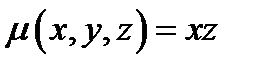
Пример 12.2. Вычислим координаты центра масс части поверхности полусферы , вырезанной цилиндром , если плотность .

Решение. Построим заданные поверхности и выделим нужную часть полусферы (на рис. 12.2 она выделена синим цветом). Поверхность удобно проецируется на плоскость в область, ограниченную окружностью .

Рисунок 12.2

Используя формулы (12.5) и (12.1) составим интеграл для вычисления массы части поверхности.

где .

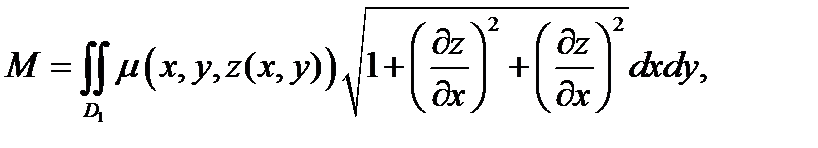
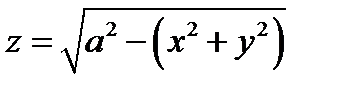
Вычислим частные производные.

.

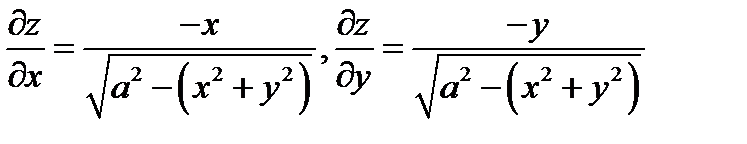
Упростим подкоренное выражение и получим интеграл

Выберем способ его вычисления. В данном случае удобнее перейти к полярным координатам и учесть симметрию относительно оси .

Составим повторный интеграл и вычислим его:

.

Далее, по формулам (12.6) вычисляем координаты центра масс. С учётом симметрии поверхности и функции плотности, без вычисления определяем, что ордината центра масс равна нулю. Для двух других координат составляем интегралы и вычисляем их.

.

.

Ответ: С .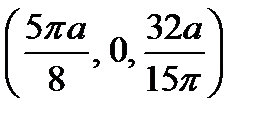

Занятие 13. Понятие гладкой и кусочно-гладкой поверхности. Ориентированные поверхности и их ориентация. Нормаль к поверхности. Определение поверхностного интеграла второго рода, его свойства. Вычисление поверхностного интеграла второго рода с помощью двойного ин-теграла. Физический смысл поверхностного интеграла второго рода.ОЛ-1гл.6, ОЛ-2 гл.3, ОЛ-4§ 12.

Практика: ОЛ-6 №№ 2350, 2351 (№ 2351 решить двумя способами: 1) с помощью вычисления составных интегралов, 2) сведением к поверхностному интегралу 1-го рода) или: ОЛ-5 №№ 10.84, 85, 87, 94.

Домашнее задание к занятию 13:

ОЛ-6 № 2349 (решить двумя способами) или ОЛ-5 №№ 10.83, 86, 88.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Студент — человек, постоянно откладывающий неизбежность. 10578 — | 7333 — или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Прежде, чем Вы начнёте скачивать свои варианты, попробуйте решить задачу по образцу, приведённому ниже для варианта 30.

&nbsp &nbsp &nbsp &nbsp Вариант 1 &nbsp &nbsp Вариант 2 &nbsp &nbsp Вариант 3 &nbsp &nbsp Вариант 4 &nbsp &nbsp Вариант 5 &nbsp &nbsp Вариант 6

&nbsp &nbsp &nbsp &nbsp Вариант 7 &nbsp &nbsp Вариант 8 &nbsp &nbsp Вариант 9 &nbsp &nbsp Вариант 10 &nbsp &nbsp Вариант 11 &nbsp &nbsp Вариант 12

&nbsp &nbsp &nbsp &nbsp Вариант 13 &nbsp &nbsp Вариант 14 &nbsp &nbsp Вариант 15 &nbsp &nbsp Вариант 16 &nbsp &nbsp Вариант 17 &nbsp &nbsp Вариант 18

&nbsp &nbsp &nbsp &nbsp Вариант 19 &nbsp &nbsp Вариант 20 &nbsp &nbsp Вариант 21 &nbsp &nbsp Вариант 22 &nbsp &nbsp Вариант 23 &nbsp &nbsp Вариант 24

&nbsp &nbsp &nbsp &nbsp Вариант 25 &nbsp &nbsp Вариант 26 &nbsp &nbsp Вариант 27 &nbsp &nbsp Вариант 28 &nbsp &nbsp Вариант 29 &nbsp &nbsp Вариант 30

&nbsp &nbsp &nbsp &nbsp 16.30. Тело V задано ограничивающими его поверхностями, 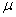&nbsp &nbsp&nbsp &nbsp — плотность. Найти массу тела.

Центр масс и моменты инерции оболочки;

Сила притяжения и сила давления;

Поток жидкости и вещества через поверхность;

Электрический заряд, распределенный по поверхности;

Электрические поля (теорема Гаусса в электростатике).

Пусть распределение массы (m) в тонкой оболочке описывается непрерывной функцией плотности (mu left(
ight).) Координаты центра масс оболочки определяются формулами [ <= frac<<>>>,>;; <= frac<<>>>,>;; <= frac<<>>>,> ] где [ <> = iintlimits_S
ight)dS> ,>;; <> = iintlimits_S
ight)dS> ,>;; <> = iintlimits_S
ight)dS> > ] − так называемые моменты первого порядка относительно координатных плоскостей (x = 0,) (y = 0) и (z = 0,) соответственно.

Моменты инерции оболочки относительно осей (Ox, Oy, Oz) выражаются, соответственно, формулами [ <= iintlimits_S <left( <+ >
ight)mu left(
ight)dS> ,>;; <= iintlimits_S <left( <+ >
ight)mu left(
ight)dS> ,>;; <= iintlimits_S <left( <+ >
ight)mu left(
ight)dS> .> ] Моменты инерции оболочки относительно плоскостей (xy, yz, xz) определяются формулами [ <> = iintlimits_S <mu left(
ight)dS> ,>;; <> = iintlimits_S <mu left(
ight)dS> ,>;; <> = iintlimits_S <mu left(
ight)dS> .> ]

Сила притяжения между поверхностью (S) и точечным телом (m) определяется выражением [mathbf = Gmiintlimits_S <mu left(
ight)frac<mathbf><<>>dS> ,] где (mathbf = left( ,y — ,z — >
ight),) (G) − гравитационная постоянная, ( <mu left(
ight)>) − функция плотности.

Предположим, что поверхность (S) задана вектором (mathbf) и находится под воздействием некоторой силы давления (это может быть плотина, крыло самолета, стенка баллона со сжатым газом и т.д.). Полная сила (mathbf,) созданная давлением (pleft( mathbf
ight),) находится с помощью поверхностного интеграла по формуле [mathbf = iintlimits_S
ight)dmathbf> .] Давление, по определению, действует в направлении вектора нормали к поверхности (S) в каждой точке. Поэтому, мы можем записать [mathbf = iintlimits_S
ight)dmathbf> = iintlimits_S dS> ,] где (mathbf) − единичный нормальный вектор к поверхности (S.)

Если в качестве векторного поля рассматривается скорость жидкости (mathbfleft( mathbf
ight),) то поток через поверхность (S) называется потоком жидкости . Он равен объему жидкости, проходящей через поверхность (S) в единицу времени и выражается формулой [Phi = iintlimits_S <mathbfleft( mathbf
ight) cdot dmathbf> .] Аналогично, поток векторного поля (mathbf =
ho mathbf,) где (
ho) − плотность, называется потоком вещества и определяется выражением [Phi = iintlimits_S <
ho mathbfleft( mathbf
ight) cdot dmathbf> .] Он численно равен массе вещества, проходящего через поверхность (S) в единицу времени.

Поток электрического смещения (mathbf) через замкнутую поверхность (S) равен алгебраической сумме всех зарядов, расположенных внутри поверхности: [Phi = iintlimits_S <mathbfcdot dmathbf> = sumlimits_i <> ,] где (mathbf = varepsilon <varepsilon _0>mathbf,) (mathbf) − напряженность электрического поля, (varepsilon) − относительная диэлектрическая проницаемость среды, ( <varepsilon _0>= 8,85 imes <10^< — 12>>, ext<Ф/м>) − диэлектрическая проницаемость вакуума.

Теорема Гаусса применима к любым замкнутым поверхностям. В случае поверхности с достаточной симметрией, данная теорема упрощает вычисление электрического поля. Теорему Гаусса рассматривают как один из основных постулатов теории электричества. Она входит в систему основных уравнений Максвелла.

Вычислим момент первого порядка (>.) [ <> = iintlimits_S
ight)dS> > = <<mu _0>iintlimits_S > = <<mu _0>iintlimits_
ight)> <1 + <><<partial x>>>
ight)>^2> + <<left( <frac<<partial z>><<partial y>>>
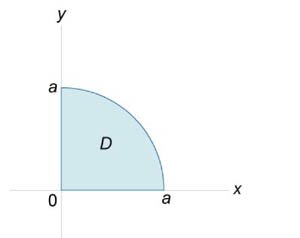
ight)>^2>> dxdy> ,> ] где проекция (
ight)>) поверхности на плоскость (xy) представляет собой часть круга, лежащую в первом квадранте (рисунок (4)).

Итак, координаты центра масс оболочки имеют вид [left( <,,>
ight) = left( <frac<2>,frac<2>,frac<2>>
ight).]

Момент инерции () находится по формуле: [ <= iintlimits_S <left( <+ >
ight)mu left(
ight)dS> > = <<mu _0>iintlimits_S <left( <+ >
ight)dS> ,> ] где поверхность (S) − это полусфера ( + + = 1;left(
ight).)

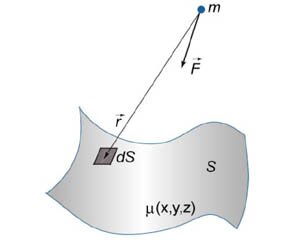
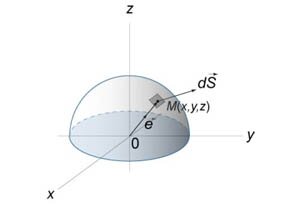
Рассмотрим точку (Mleft(
ight)) полусферы, которая принадлежит малому участку поверхности (dS) (рисунок (5)). Силу притяжения (dmathbfleft( M
ight)) между элементом поверхности (dS) и массой (m) можно записать в виде [dmathbfleft( M
ight) = frac<mdS>><<>>mathbfleft(
ight),] где (G) − гравитационная постоянная, (mathbfleft(
ight)) − единичный вектор, направленный из точки (O) в точку (M.)
Так как (mathbfleft(
ight) = left( <largefrac
ormalsize, largefrac
ormalsize, largefrac
ormalsize>
ight),) то можно записать [dmathbfleft( M
ight) = frac<mdS>><<>>left(
ight).] После интегрирования по поверхности полусферы получаем следующие выражения для компонентов силы притяжения: [ <= frac<m>><<>>iintlimits_S ,>;; <= frac<m>><<>>iintlimits_S ,>;; <= frac<m>><<>>iintlimits_S .> ] В сферических координатах уравнение полусферы записывается в виде [ <mathbfleft( <psi , heta >
ight) > = + rsin psi sin heta cdot mathbf + rcos heta cdot mathbf,> ] где (0 le psi le 2pi ,;0 le heta le largefrac<pi ><2>
ormalsize.)

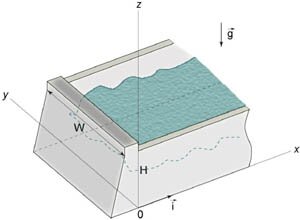
В условиях гидростатического равновесия давление на поверхность дамбы зависит от координаты (z) в соответствии с формулой [pleft( z
ight) =
ho gleft(
ight),] где (
ho) − плотность воды, (g) − ускорение свободного падения.

Полная сила давления, действующая на плотину, будет равна [ <mathbf= iintlimits_S dS> > = <intlimits_0^W <intlimits_0^H <
ho gleft(
ight) cdot left( < — mathbf>
ight)dydz> > > = <
ho gWleft( < — mathbf>
ight)left[ <left. <left( >><2>>
ight)>
ight|_0^H>
ight] > = <frac<<
ho gW>><2>left( < — mathbf>
ight).> ] Вектор (left( < — mathbf>
ight)) показывает направление действия силы (mathbf.) Абсолютное значение силы равно [left| mathbf
ight| = frac<<
ho gW>><2>.]

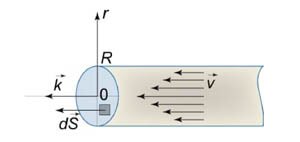
В силу симметрии системы вектор напряженности электрического поля должен быть перпендикулярен поверхности, а величина напряженности должна быть одинакова во всех точках, равноудаленных от пластины.

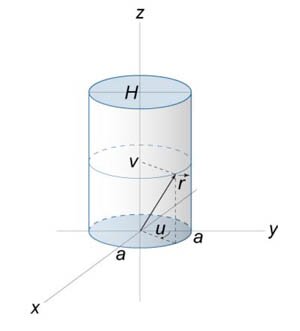
Рассмотрим условную гауссовскую поверхность в форме цилиндра с поперечным сечением (S) и высотой (2H) (рисунок (8)). Поток электрического смещения отличен от нуля лишь на основаниях цилиндра. Следовательно, (Phi = 2<varepsilon _0>ES,) где (E) − электрическое поле в основаниях цилиндра. Полный заряд внутри цилиндрической поверхности равен (Q = sigma S.) Тогда по теореме Гаусса получаем [ <Phi = <varepsilon _0>iintlimits_S = Q,>;; <Rightarrow 2<varepsilon _0>ES = sigma S;; ext<или>;;> <<2<varepsilon _0>>>.> ]