07.06.2019
5 июня Что порешать по физике
30 мая Решения вчерашних ЕГЭ по математике
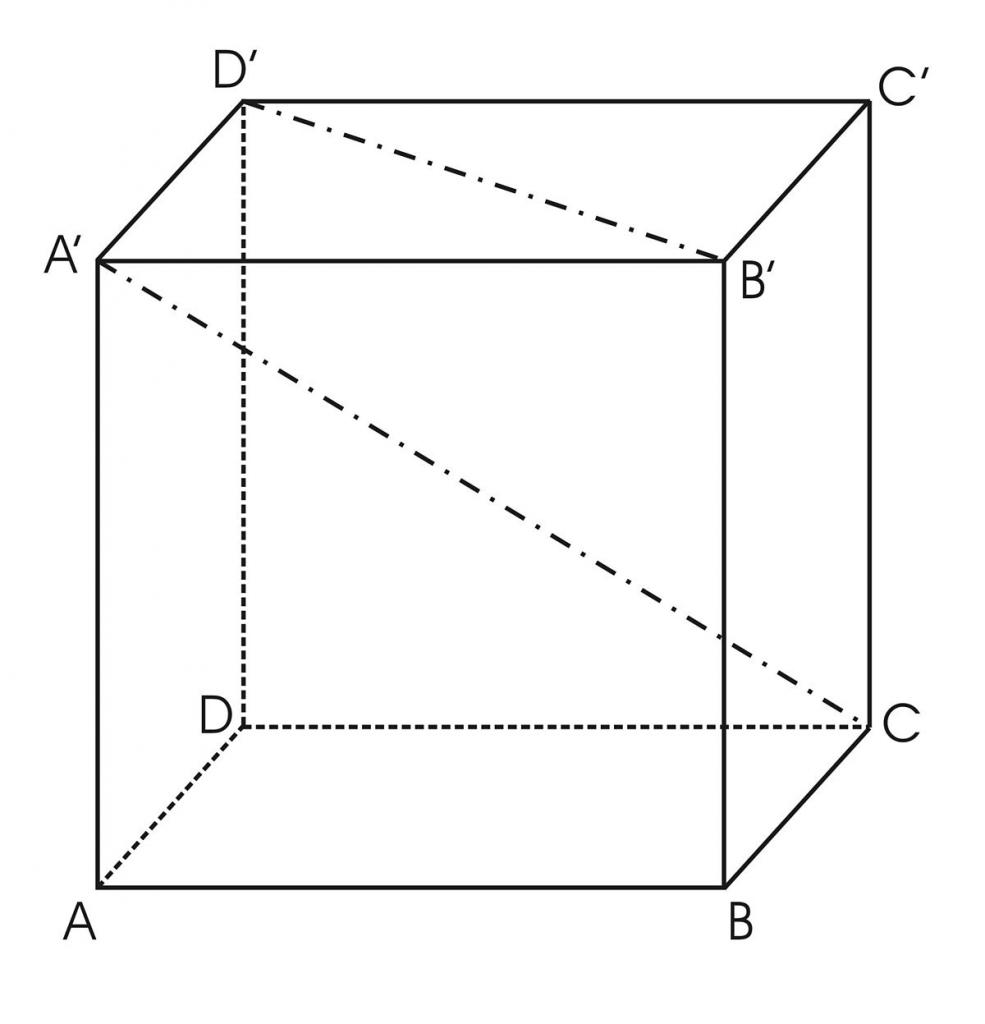
В правильной четырёхугольной призме ABCDA1B1C1D1 ребро AA1 равно 15, а диагональ BD1 равна 17. Найдите площадь сечения призмы плоскостью, проходящей через точки A, A1 и C.
Диагональное сечение прямой призмы — прямоугольник Диагонали правильной четырёхугольной призмы равны:
По теореме Пифагора получаем:
Тем самым, для искомой площади сечения имеем
а почему 120? нам же надо найти площадь треугольника АА1С а не прямоугольника АА1СС1. ответьте пожалуйста
Плоскости, в частности, плоскости сечения, обычно обозначаются тремя буквами. В сечении при этом вовсе не обязательно будет треугольник. Поэтому необходимо сначала выяснить, какой многоугольник будет являться сечением, а затем искать его площадь.
Призма является геометрической объемной фигурой, характеристики и свойства которой изучают в старших классах школ. Как правило, при ее изучении рассматривают такие величины, как объем и площадь поверхности. В данной же статье раскроем несколько иной вопрос: приведем методику определения длины диагоналей призмы на примере четырехугольной фигуры.
Какая фигура называется призмой?
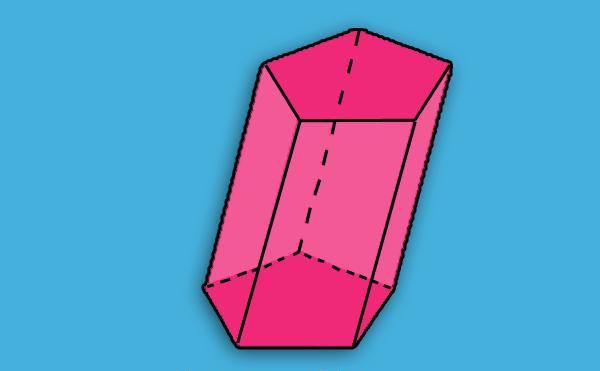
В геометрии дается следующее определение призме: это объемная фигура, ограниченная двумя многоугольными одинаковыми сторонами, которые параллельны друг другу, и некоторым числом параллелограммов. Рисунок ниже показывает пример призмы, соответствующий данному определению.
Мы видим, что два красных пятиугольника равны друг другу и находятся в двух параллельных плоскостях. Пять розовых параллелограммов соединяют эти пятиугольники в цельный объект — призму. Два пятиугольника называются основаниями фигуры, а ее параллелограммы — это боковые грани.
Призмы бывают прямые и наклонные, которые также называют прямоугольными и косоугольными. Разница между ними заключается в углах между основанием и боковыми гранями. Для прямоугольной призмы все эти углы равны 90 o .
По количеству сторон или вершин многоугольника в основании говорят о призмах треугольных, пятиугольных, четырехугольных и так далее. Причем если этот многоугольник является правильным, а сама призма прямой, то такую фигуру называют правильной.
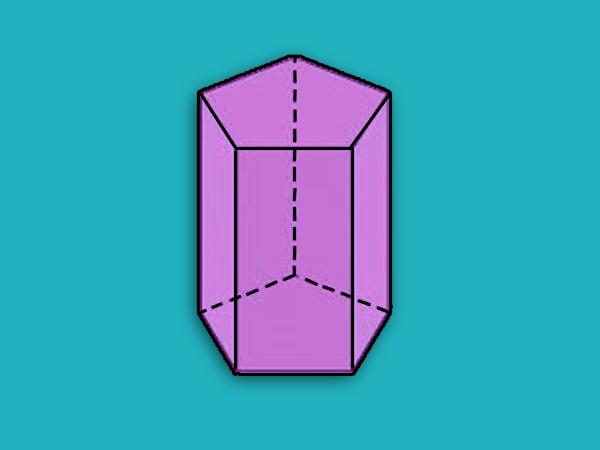
Приведенная на предыдущем рисунке призма является пятиугольной наклонной. Ниже же изображена пятиугольная прямая призма, которая является правильной.
Все вычисления, включая методику определения диагоналей призмы, удобно выполнять именно для правильных фигур.
Какие элементы характеризуют призму?
Элементами фигуры называют составные части, которые ее образуют. Конкретно для призмы можно выделить три главных типа элементов:
Гранями считаются основания и боковые плоскости, представляющие параллелограммы в общем случае. В призме всегда каждая сторона относится к одному из двух типов: либо это многоугольник, либо параллелограмм.
Ребра призмы — это те отрезки, которые ограничивают каждую сторону фигуры. Как и грани, ребра также бывают двух типов: принадлежащие основанию и боковой поверхности или относящиеся только к боковой поверхности. Первых всегда в два раза больше, чем вторых, независимо от вида призмы.
Вершины — это точки пересечения трех ребер призмы, два из которых лежат в плоскости основания, а третье — принадлежит двум боковым граням. Все вершины призмы находятся в плоскостях оснований фигуры.
Числа описанных элементов связаны в единое равенство, имеющее следующий вид:
Здесь Р — количество ребер, В — вершин, С — сторон. Это равенство называется теоремой Эйлера для полиэдра.
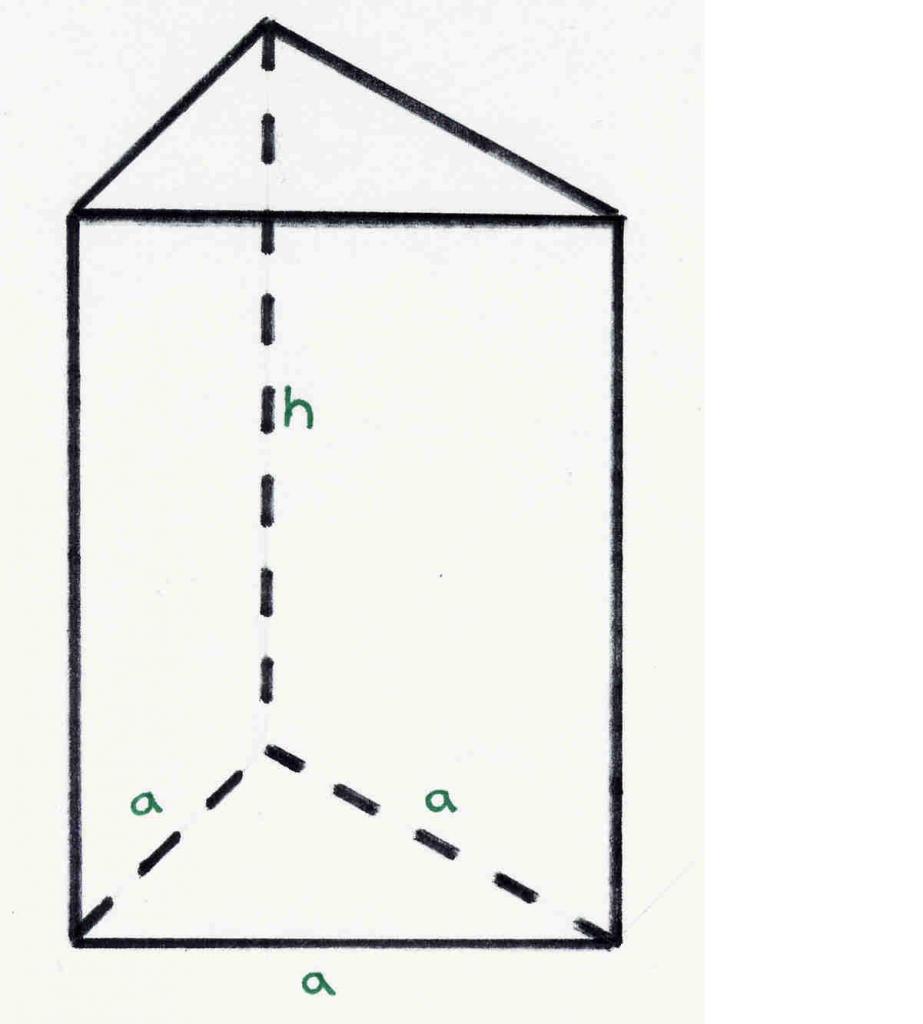
На рисунке показана треугольная правильная призма. Каждый может посчитать, что она имеет 6 вершин, 5 сторон и 9 ребер. Эти цифры согласуются с теоремой Эйлера.
Диагонали призмы
После таких свойств, как объем и площадь поверхности, в задачах по геометрии часто встречается информация о длине той или иной диагонали рассматриваемой фигуры, которая либо дана, либо ее нужно найти по другим известным параметрам. Рассмотрим, какие бывают диагонали у призмы.
Все диагонали можно разделить на два типа:
- Лежащие в плоскости граней. Они соединяют несоседние вершины либо многоугольника в основании призмы, либо параллелограмма боковой поверхности. Значение длин таких диагоналей определяется, исходя из знания длин соответствующих ребер и углов между ними. Для определения диагоналей параллелограммов всегда используются свойства треугольников.
- Лежащие внутри объема призмы. Эти диагонали соединяют неоднотипные вершины двух оснований. Эти диагонали оказываются полностью внутри фигуры. Их длины рассчитать несколько сложнее, чем для предыдущего типа. Методика расчета предполагает учет длин ребер и основания, и параллелограммов. Для прямых и правильных призм расчет является относительно простым, поскольку он осуществляется с использованием теоремы Пифагора и свойств тригонометрических функций.
Далее приведем примеры вычисления различных диагоналей.
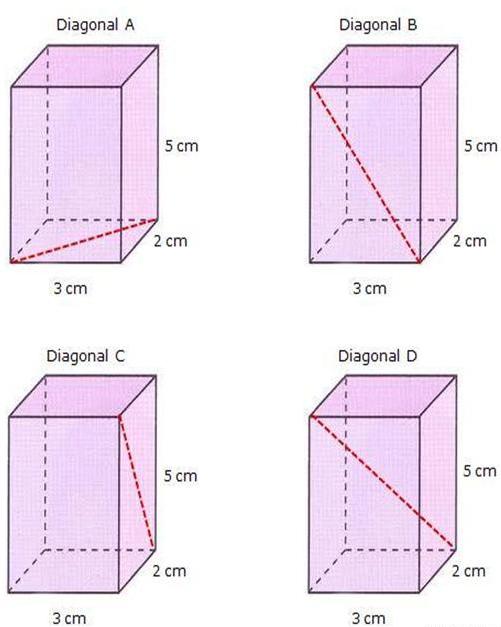
Диагонали сторон четырехугольной прямой призмы
На рисунке выше изображены четыре одинаковые прямые призмы, и даны параметры их ребер. На призмах Diagonal A, Diagonal B и Diagonal C штриховой красной линией изображены диагонали трех разных граней. Поскольку призма является прямой с высотой 5 см, а ее основание представлено прямоугольником со сторонами 3 см и 2 см, то отыскать отмеченные диагонали не представляет никакого труда. Для этого необходимо воспользоваться теоремой Пифагора.
Длина диагонали основания призмы (Diagonal A) равна:
DA = √(3 2 +2 2 ) = √13 ≈ 3,606 см.
Для боковой грани призмы диагональ равна (см. Diagonal B):
DB = √(3 2 +5 2 ) = √34 ≈ 5,831 см.
Наконец, длина еще одной боковой диагонали равна (см. Diagonal C):
DС = √(2 2 +5 2 ) = √29 ≈ 5,385 см.
Длина внутренней диагонали
Теперь рассчитаем длину диагонали четырехугольной призмы, которая изображена на предыдущем рисунке (Diagonal D). Сделать это не так сложно, если заметить, что она является гипотенузой треугольника, в котором катетами будут высота призмы (5 см) и диагональ DA , изображенная на рисунке вверху слева (Diagonal A). Тогда получаем:
DD = √(DA 2 +5 2 ) = √(2 2 +3 2 +5 2 ) = √38 ≈ 6,164 см.
Правильная призма четырехугольная
Диагональ правильной призмы, основанием которой является квадрат, рассчитывается аналогичным образом, как и в приведенном выше примере. Соответствующая формула имеет вид:
Где a и c — длины стороны основания и бокового ребра, соответственно.
Заметим, что при вычислениях мы использовали только теорему Пифагора. Для определения длин диагоналей правильных призм с большим числом вершин (пятиугольные, шестиугольные и так далее) уже необходимо применять тригонометрические функции.
Призма — многогранник, 2 грани это конгруэнтные (равные) многоугольники, которые лежат в
параллельных плоскостях, а оставшиеся грани — параллелограммы, имеющие общие стороны с
этими многоугольниками. Либо (что тоже самое) — это многогранник, основаниями которого
являются равные многоугольники, а боковыми гранями — параллелограммы.
Призма является разновидностью цилиндра.
Элементы призмы.
конгруэнтными многоугольниками, которые лежат
в плоскостях, параллельных друг другу.
Боковые грани (ABLK, BCML, CDNM, DEPN, EAKP) – каждая
из граней, не считая оснований. Все боковые грани – это
Боковая поверхность – сумма боковых граней.
Полная поверхность – сумма основания и боковой
Боковые ребра (AK, BL, CM, DN, EP) – общие стороны

Высота (KR) – отрезок, который соединяет плоскости, в них лежат основания призмы. Он
перпендикулярен этим плоскостям.
Диагональ (BP) – отрезок, который соединяет 2 вершины призмы, которые не принадлежат одной
Диагональная плоскость – плоскость, которая проходит через боковое ребро призмы, а также
Диагональное сечение (EBLP) – пересечение призмы и диагональной плоскости. В сечении получается
Перпендикулярное (ортогональное) сечение – пересечение призмы и плоскости, перпендикулярной
боковому ребру призмы.
Свойства призмы.
- Основания призмы – это равные многоугольники.
- Боковые грани призмы имеют вид параллелограмма.
- Боковые ребра призмы параллельные и равны.
- Площадь полной поверхности призмы = сумме площади её боковой поверхности и двойной
где P — периметр перпендикулярного сечения, l — длина бокового ребра.
- Площадь боковой поверхности прямой призмы:
где P — периметр основания призмы, h — высота призмы.
- Перпендикулярное сечение перпендикулярно всем боковым рёбрам призмы.
- Углы перпендикулярного сечения — это линейные углы двугранных углов при соответствующих
- Перпендикулярное сечение перпендикулярно всем боковым граням.
- Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
где V — объем призмы,
So — площадь основания призмы,
h — высота призмы.

Привальная четырехугольная пирамида.
Свойства правильной четырехугольной призмы.
- Основания правильной четырехугольной призмы – это 2 одинаковых квадрата;
- Верхнее и нижнее основания параллельны;
- Боковые грани имеют вид прямоугольников;
- Все боковые грани равны между собой;
- Боковые грани перпендикулярны основаниям;
- Боковые ребра параллельны между собой и равны;
- Перпендикулярное сечение перпендикулярно всем боковым ребрам и параллельно основаниям;
- Углы перпендикулярного сечения — прямые;
- Диагональное сечение правильной четырехугольной призмы является прямоугольником;
- Перпендикулярное (ортогональное сечение) параллельно основаниям.
Формулы для правильной четырехугольной призмы.
Виды призм.
Призма, у которой в основании лежит параллелограмм, является параллелепипедом.
Прямая призма — это призма, с перпендикулярными боковыми ребрами относительно плоскости основания.
Остальные призмы являются наклонными.
Правильная призма — прямая призма, в основании у нее лежит правильный многоугольник. Боковые
грани такой призмы — одинаковые прямоугольники.
Правильная призма, у которой боковые грани – квадраты (высота равна стороне основания), называется
полуправильным многогранником.