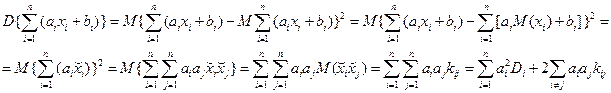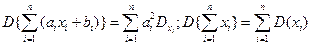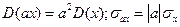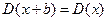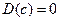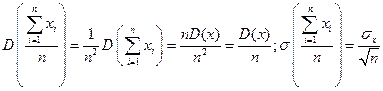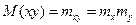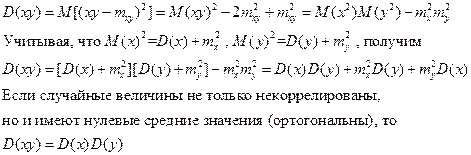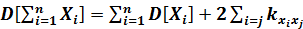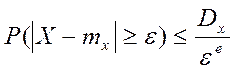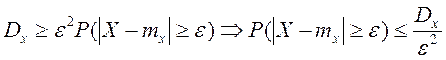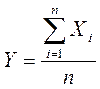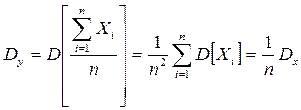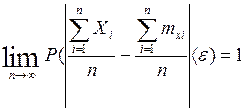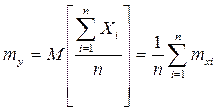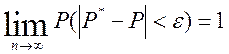О законе больших чисел
Дисперсия линейной функции случайных аргументов
В случае попарно некоррелированных величин 
Для некоррелированных величин с равными дисперсиями дисперсия среднего арифметического равна
Для некоррелированных величин 
Дисперсия произведения некоррелированных случайных величин
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8833 — 
| 7546 — 
или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Математическое ожидание произведения двух случайных величин равно произведению их математических ожиданий плюс корреляционный момент:
. (10.2.17)
Доказательство. Будем исходить из определения корреляционного момента:
,
; 
.
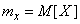
Преобразуем это выражение, пользуясь свойствами математического ожидания:
,
что, очевидно, равносильно формуле (10.2.17).
Если случайные величины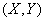 
некоррелированны 
, то формула (10.2.17) принимает вид:
, (10.2.18)
т. е. математическое ожидание произведения двух некоррелированных случайных величин равно произведению их математических ожиданий.
Это положение известно под названием теоремы умножения математических ожиданий.
Формула (10.2.17) представляет собой не что иное, как выражение второго смешанного центрального момента системы через второй смешанный начальный момент и математические ожидания:
. (10.2.19)
Это выражение часто применяется на практике при вычислении корреляционного момента аналогично тому, как для одной случайной величины дисперсия часто вычисляется через второй начальный момент иматематическое ожидание.
Теорема умножения математических ожиданий обобщается и на произвольное число сомножителей, только в этом случае для ее применения недостаточно того, чтобы величины были некоррелированны, а требуется, чтобы обращались в нуль и некоторые высшие смешанные моменты, число которых зависит от числа членов в произведении. Эти условия заведомо выполнены при независимости случайных величин, входящих в произведение. В этом случае
, (10.2.20)
т. е. математическое ожидание произведения независимых случайных величин равно произведению ихматематических ожиданий.
Это положение легко доказывается методом полной индукции.
Дисперсия произведения независимых случайных величин
Докажем, что для независимых величин 
. (10.2.21)
Доказательство. Обозначим 
. По определению дисперсии
.
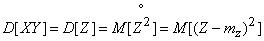
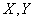
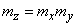
Так как величины независимы, 
и
.
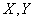
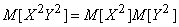
При независимых величины 
тоже независимы; следовательно,
, 
. (10.2.22)
Но 
есть не что иное, как второй начальный момент величины 
, и, следовательно, выражается через дисперсию:
;
.
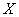
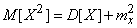
Подставляя эти выражения в формулу (10.2.22) и приводя подобные члены, приходим к формуле (10.2.21).
В случае, когда перемножаются центрированные случайные величины (величины с математическими ожиданиями, равными нулю), формула (10.2.21) принимает вид:
, (10.2.23)
т. е. дисперсия произведения независимых центрированных случайных величин равна произведению их дисперсий.
Высшие моменты суммы случайных величин
В некоторых случаях приходится вычислять высшие моменты суммы независимых случайных величин. Докажем некоторые относящиеся сюда соотношения.
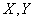
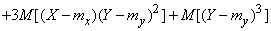
1) Если величины независимы, то
. (10.2.24)
,
откуда по теореме умножения математических ожиданий
.
Но первый центральный момент 
для любой величины равен нулю; два средних члена обращаются в нуль, и формула (10.2.24) доказана.
Соотношение (10.2.24) методом индукции легко обобщается на произвольное число независимых слагаемых:
. (10.2.25)
2) Четвертый центральный момент суммы двух независимых случайных величин выражается формулой
. (10.2.26)
где 
— дисперсии величин и 
.
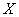
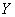
Доказательство совершенно аналогично предыдущему.
Методом полной индукции легко доказать обобщение формулы (10.2.26) на произвольное число независимых слагаемых:
. (10.2.27)
Аналогичные соотношения в случае необходимости легко вывести и для моментов более высоких порядков.
Теорема 1.Дисперсия суммы СВ равна сумме дисперсий этих величин плюс удвоенная сумма корреляционных моментов каждой из слагаемых величин со всеми последующими
Следствие 1.Дисперсия суммы некоррелированных СВ равна сумме дисперсий слагаемых
Теорема 2. Дисперсия произведения двух независимых случайных величин вычисляется по формуле.
Следствие. Дисперсия произведения независимых центрированных СВ равно произведению их дисперсии.
ТЕМА 5. ЗАКОН БОЛЬШИХ ЧИСЕЛ И ПРЕДЕЛЬНЫЕ
ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ.
Предельные теоремы теории вероятностей.
Группа теорем, устанавливающих соответствие между теоретическими и экспериментальными характеристиками СВ и случайных событий при большом числе испытаний над ними, а также касающихся предельных законов распределения, объединяются под общим названием предельных теорем теории вероятностей.
В настоящей лекции мы познакомимся с двумя типами предельных теорем: законом больших чисел и центральной предельной теоремой.
Закон больших чисел, занимающий важнейшее место в теории вероятностей, является связующим звеном между теорией вероятностей как математической наукой и закономерностями случайных явлений при массовых наблюдениях над ними.
2. Закон больших чисел: теорема Чебышева, теорема Маркова.
Рассмотрим СВ Х, МОЖ которой mх и дисперсия Dх.
Неравенство Чебышева утверждает: вероятность того, что
отклонение случайной величины от ее МОЖ будет по абсолютной величин не меньше любого положительного числа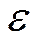 
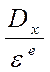
, ограничена сверху величиной 
.
Доказательство: 1. Пусть СВ Х дискретное с рядом распределения
| Хк | Х1 | Х2 | … | Хn |
| Рк | Р1 | Р2 | … | Рn |
тогда дисперсия СВ Х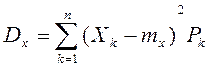 
.
Очевидно, что слагаемые этой суммы не отрицательны. Отбросим те слагаемые, у которых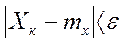 
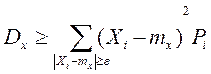
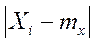
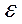
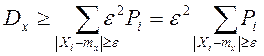
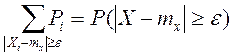
,вследствие чего сумма может только уменьшиться, т.е. 
, заменим 
через 
, то после этой замены å может только уменьшиться.
, но 
.
Т.о. 
2. Пусть СВ Х непрерывна с плотностью распределения f(х).
Тогда 
выделим на числовой оси
, заменяя 
через 
, опять уменьшаем величину интеграла 
, но
, следовательно 
.
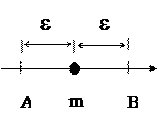
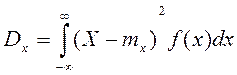
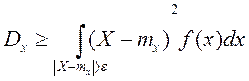
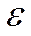
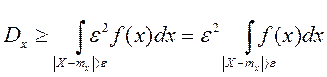
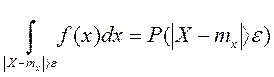
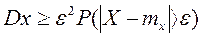
Здесь знак ³ заменен знак >, так как для непрерывной СВ вероятность точного равенства рана 0.
Теорема ЧЕБЫШЕВА. При неограниченном увеличении числа независимых испытаний среднее арифметическое наблюдаемых значений СВ, имеющей конечную дисперсию, сходится по вероятности к ее математическому ожиданию.
Доказательство: рассмотрим СВ 
Применим к СВ Y неравенства 
Чебышева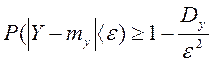 
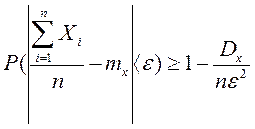
или 
.
Перейдя к пределу, учитывая, что Р£1 и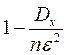 
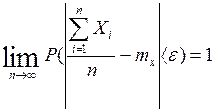
®1 при n®¥
Теорема доказана.
Обобщенная теорема Чебышева. При неограниченном увеличении числа независимых испытаний над СВ, имеющим ограниченные дисперсии, среднее арифметическое наблюдаемых значений сходится по вероятности к среднему арифметическому МОЖ этих величин, т.е.
Доказательство: Рассмотрим СВ 
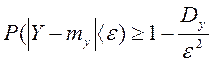
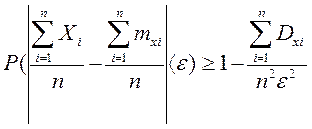
Применяя к СВ Y неравенство Чебышева получим или 
.
Из ограниченности дисперсий следует, что существует такое постоянное С, для которого Dxi
Теорема Маркова. Если имеются зависимые СВ Х1, Х2, …, Хn и если при n®¥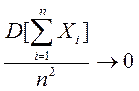 
, то среднее арифметическое наблюдаемых значений СВ Х1, Х2, …, Хn сходится по вероятности к среднему арифметическому их МОЖ.
Доказательство: Рассмотрим СВ 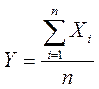, очевидно
Dy=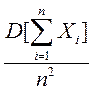 
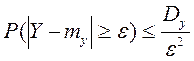
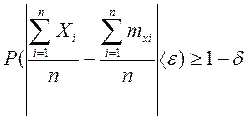
. Применим с СВ Y неравенство Чебышева
. Так как по условию теоремы при n®¥, Dy®0, то при достаточно большом n 
, где d, e — сколь угодно малая положительная величина, или переходя к противоположному событию
. Теорема доказана.
3. Следствия закона больших чисел: теоремы Бернулли и Пуассона.
Теорема Я.Бернулли является важнейшей и исторически первой формой закона больших чисел. Он устанавливает связь между частотой события и его вероятностью. Доказательство данное Бернулли было весьма сложным. Простое доказательство дано П.П. Чебышевым – как прямое следствие из его теоремы.
Теорема Бернулли. При неограниченном увеличении числа независимых опытов в постоянных условиях чистоты рассматриваемого события АР * сходится по вероятности к его вероятности Р в отдельном опыте.
Доказательство: Обозначим Х1 – СВ – число появлений события А в первом опыте, Х2 – СВ – число появлений события А во втором опыте и т.д.
Каждая из величины Хi(i=1, 2, …, n) есть дискретное СВ с двумя возможными значениями 0 и 1. Ряд распределения СВ Хi имеет вид
| Хi | ||
| Рi | q | Р |
, где q=1-Р – вероятность не появления А.
Математическое ожидание каждой из величин Хi равно р, а ее дисперсия qр.
Частота Р * представляет собой среднее арифметическое СВ Х1,Х2, …, Хn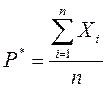 
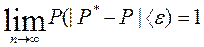
. Применим к этим величинам теорему Чебышева получим
.
Обобщением теоремы Бернулли на случай, когда опыты происходят при неодинаковых условиях, является теорема Пуассона, которая формулируется следующим образом.
Теорема Пуассона. При неограниченном увеличении числа независимых опытов в переменных условиях чистоты события А сходится по вероятности к среднему арифметическому его вероятностей Рi при данных испытаниях.
Доказательство теоремы Пуассона следует из обобщенной теоремы Чебышева, точно также, как доказательство теоремы Бернулли следует из теоремы Чебышева.
Дата добавления: 2016-03-05 ; просмотров: 1183 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ