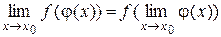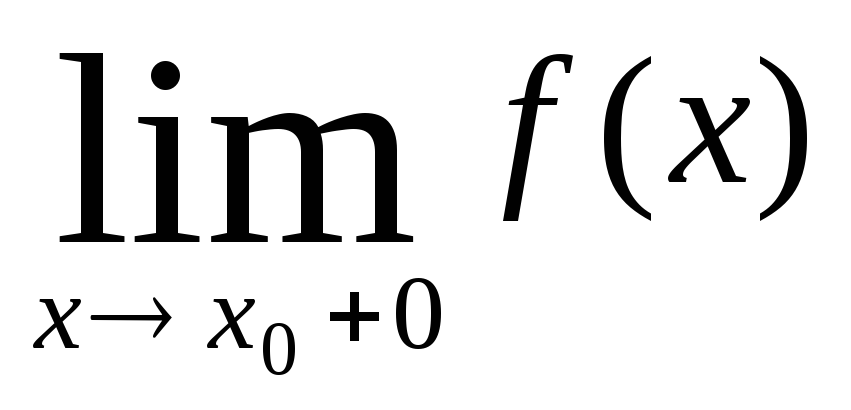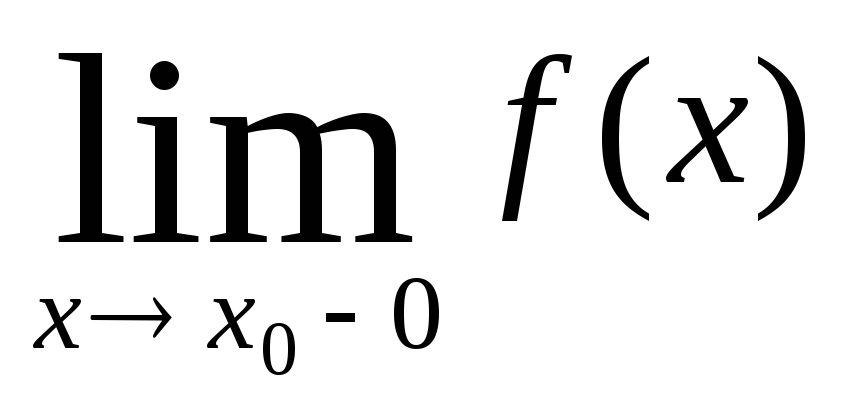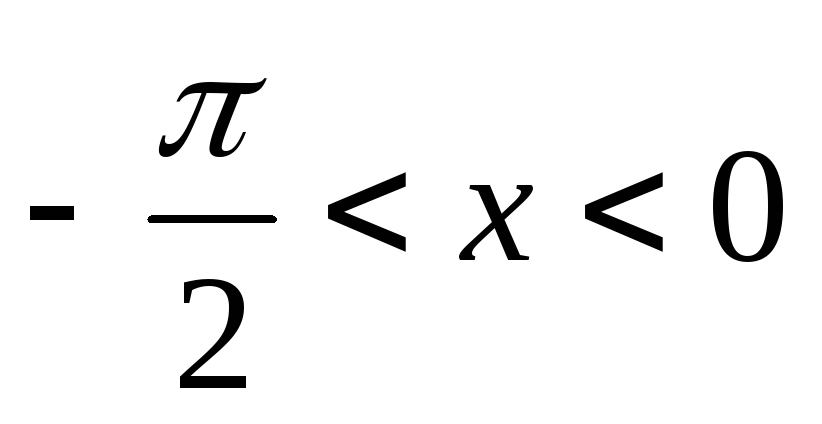Лекция 3. Непрерывность функции
Содержание лекции: Непрерывность функции в точке. Точки разрыва, их классификация. Непрерывность элементарных функций.
Свойства функций, непрерывных в точке и на отрезке.
Асимптоты графика функции.
1. непрерывность функции в точке.
С понятием предела связано другое важное понятие математического анализа – понятие непрерывности функции.
Когда мы давали определение предела функции в точке х0, то отмечали, что х0 – предельная точка области определения функции – может и не принадлежать этой области. Кроме того, когда говорили, что х стремится к х0, не требовали, чтобы х = х0, хотя при вычислении предела прежде всего вычисляли значение функции в предельной точке. Особый интерес представляет именно случай, когда х0ÎD(f) , х принимает значение х0 и 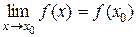
Определение 3.1. Пусть х0 – точка из области определения функции. Функция у = f(x) называется непрерывной в точке х0 , если

Если это условие не выполняется, то функция имеет разрыв в точке х0
Согласно теореме 2.1(критерию существования предела), 
Теорема 3.1.(Критерий непрерывности)
Функция f(x) непрерывна в точке х0 тогда и только тогда, когда функция определена в этой точке, существуют конечные односторонние пределы f(x0+0) и f(x0–0) и выполняется равенство
Отсюда следует алгоритм исследования непрерывности функции в заданной точке:
2) проверить существование конечных односторонних пределов f(x0+0) и f(x0–0);
Если все условия выполнены, то функция в точке х0 непрерывна.
Если хотя бы одно условие нарушено, то функция в точке х0 терпит разрыв.
Определение 3.2.
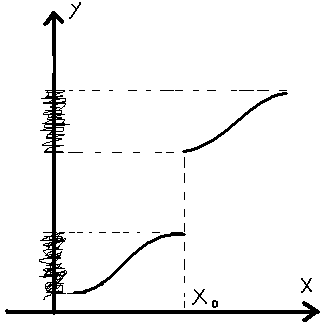
Точка х0 называется точкой разрыва первого рода (разрыва с конечным скачком), если существуют конечные односторонние пределы f(x0+0) и f(x0–0) , но f(x0+0) ¹ f(x0–0).
Точка х0 называется точкой разрыва второго рода, если хотя бы один из односторонних пределов не существует (например, равен ¥).
Точка х0 называется точкой устранимого разрыва, если существуют конечные пределы f(x0+0) и f(x0–0) и
Из сформулированного выше алгоритма и определения 3.2 следует, что если не выполнено первое условие алгоритма (функция в точке х0 не определена), то можно только сделать вывод, что в этой точке функция терпит разрыв. Характер же разрыва определяется при проверке условий 2 – 4 алгоритма.
если не выполнено условие 2, то разрыв – второго рода (рис 8 а, б, в).
Если не выполнено условие 3, а условие 2 выполнено, то разрыв – первого рода, при этом условие 1 может быть выполнено (рис.9, а, в), а может быть и не выполнено (рис.9, б). В случае разрыва первого рода число
называется скачком функции в точке х0.
 |
| Рис.9 |

Дадим еще одно определение непрерывности функции в точке. Для этого введем следующую терминологию. Если при своем изменении переменная х от значения х0 перешла к значению х1, то говорят, что х получила приращение
При этом функция у = f(x) также получит приращение
Определение 3. 3.Функция у = f(x) называется непрерывной в точке х0 , если х0Î D(f) и малому приращению функции соответствует малое приращение аргумента, т.е.

Можно доказать, что определения 3.1 и 3.3 эквивалентны. Действительно, если, то " e > 0 $ d > 0 такое, что "х, |x – x0| 0 $ d > 0 такое, что "х, |Dх | 0 $ d > 0 такое, что "х, |Dх | 0 $ d > 0 такое, что "х, |x – x0|
Тогда 
Аналогично, для функции у = sinx, xÎ R. получаем для любого х:

что также означает непрерывность функции у = sinx в произвольной точке х области определения.
Для остальных элементарных функций доказательство аналогично.
Если функции f(x) и g(x) определены в области D и непрерывны в точке х0ÎD, то в этой точке также непрерывны функции f(x) .g(x), f(x) ± g(x), 
Доказательство: Эти утверждения следуют непосредственно из определения непрерывной в точке функции и свойств пределов (теорема 2.5).
Например, если функции f(x) и g(x) непрерывны в точке х0, то 
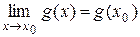

что и означает непрерывность частного в точке х0.
Непрерывность суммы, разности и частного доказать самостоятельно.
Пусть функция j(х) определена на множестве D, а функция f(у) определена на множестве Е(j). Если j(х) непрерывна в точке х0ÎD, а f(у) непрерывна в точке у0 = j(х0), то сложная функция f(j(x)) непрерывна в точке х0. (без доказательства)
Учитывая определение элементарной функции, из теорем 3.2, 3.3 и 3.4. получаем
Всякая элементарная функция непрерывна в каждой точке, в которой она определена.
Таким образом, областью непрерывности всякой элементарной функции является ее область определения.
Из теоремы 3.4 следует еще одно важное свойство – возможность перехода к пределу под знаком функции:

Дата добавления: 2016-11-02 ; просмотров: 3497 | Нарушение авторских прав
Так как функция у = х непрерывна в любой точке, по теореме о непрерывности произведения непрерывных функций, функция у = х 2 – непрерывная. Последовательно применяя вышеупомянутую теорему, получаем, что для любого натурального m функция у = x m – непрерывна. Умножая непрерывные функции e = x, x 2 , a 3 , …, x k на постоянные числа с1, с2, …, сk соответственно, получаем, что c1x, c2x 2 , …, ckx k – непрерывные функции. Сложив c0 + c1x + … + ckx k получаем непрерывную функцию. Итак, многочлен – непрерывная на всей прямой функция.
Непрерывность рациональной функции
По определению, рациональной функцией R(x) называется отношение двух многочленов, P(x) и Q(x), т. е. R(x) = 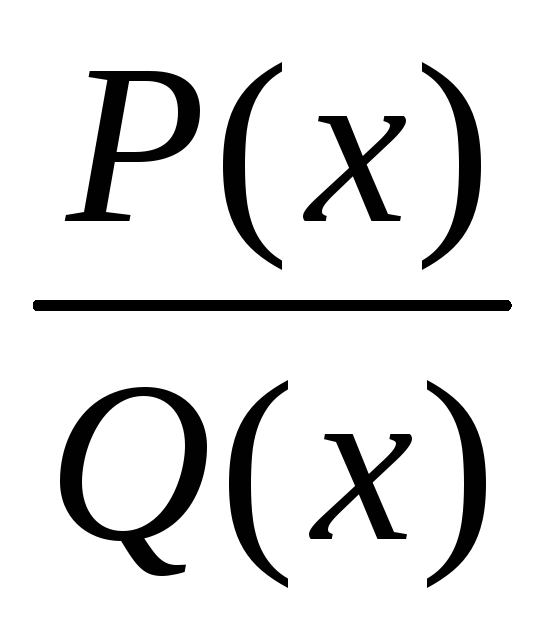
Во всех тех точках x0, где Q(x) ≠ 0, функция R(x) непрерывна по теореме о непрерывности частного. Если же в точке x0 выполняется равенство Q(x0) = 0, то в этой точке может быть устранимый разрыв, как например, в точке x0 = 1 у функции 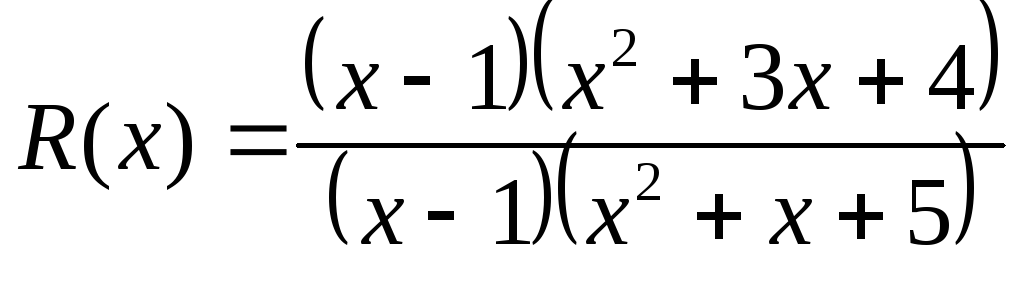
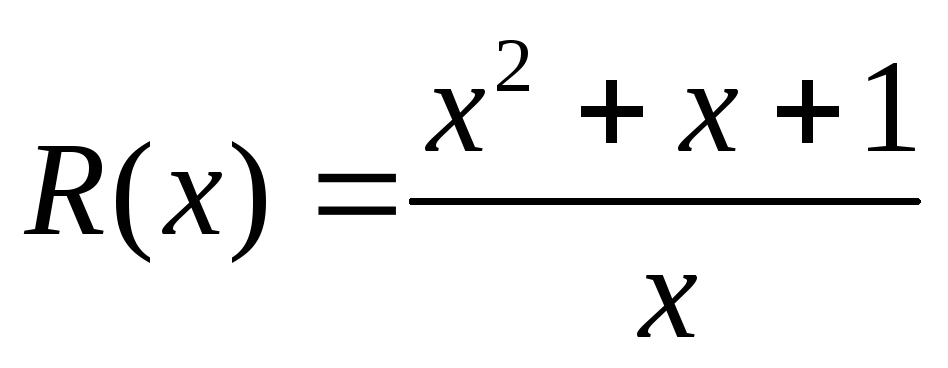
Для дальнейшего исследования будет полезной следующая теорема.
Для доказательства вспомним, что если f(x) строго монотонна на промежутке X, то, согласно следствию теоремы 10.2, в любой внутренней точке x0 этого промежутка существуют 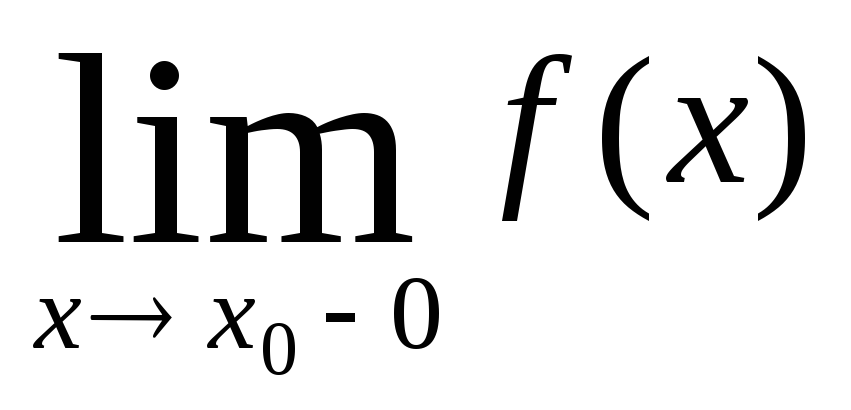
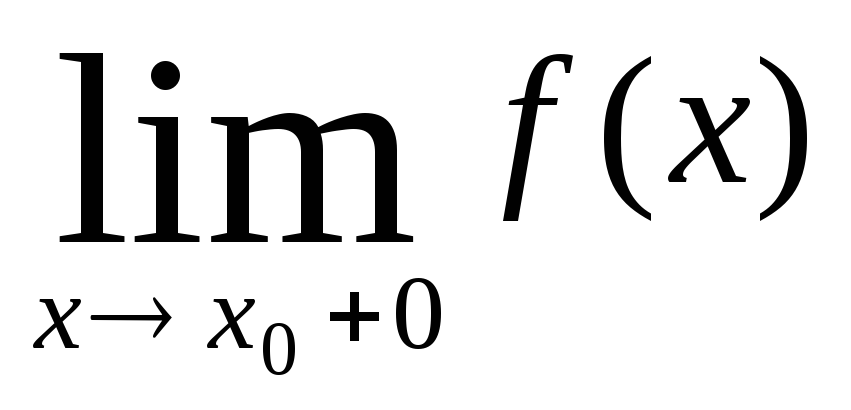
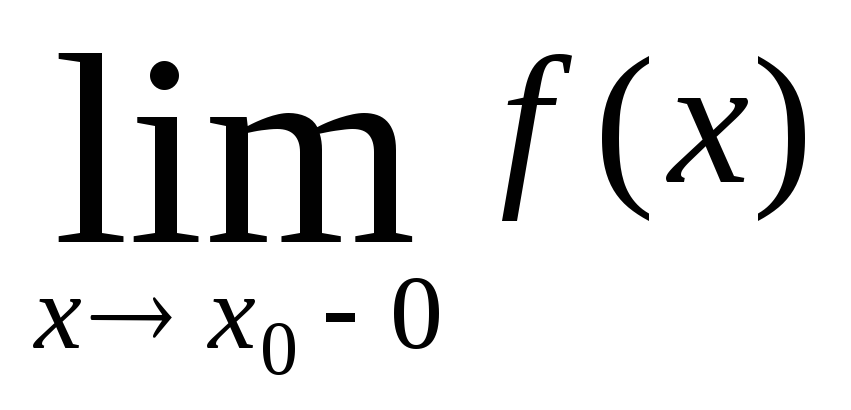
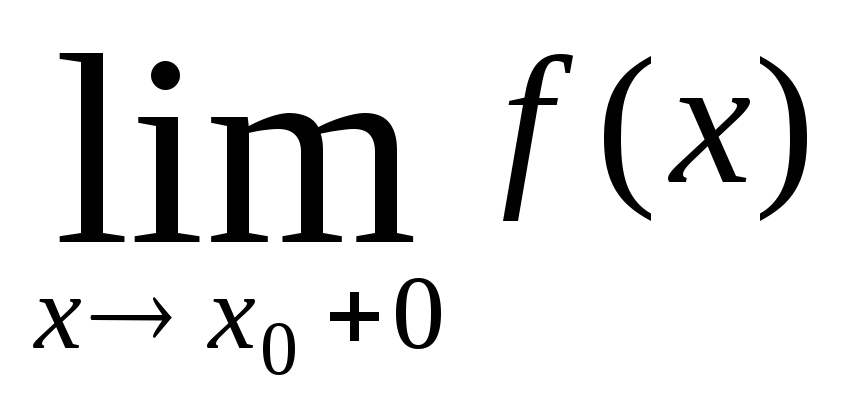
3. Непрерывность показательной функции
Функция y=a x монотонна (возрастает при a>1, убывает при 0 x непрерывна на всей числовой оси.
4. Непрерывность логарифмической функции
Функция logax монотонна (возрастает при a>1, убывает при 0
Функция y=x определена при x>0, причем x = e ln x . По доказанному, z = ln x — непрерывная функция при x>0, функция y = e z непрерывна при всех z, поэтому, по теореме о непрерывности сложной функции, y = x — непрерывная при x>0 функция.
При вычислении предела 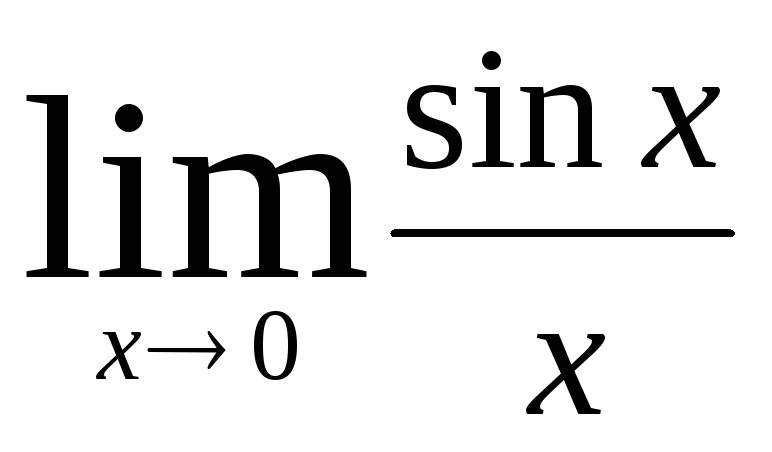
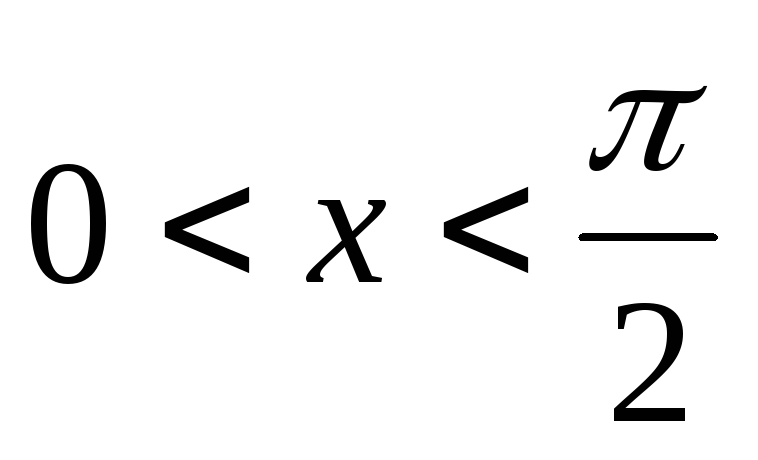
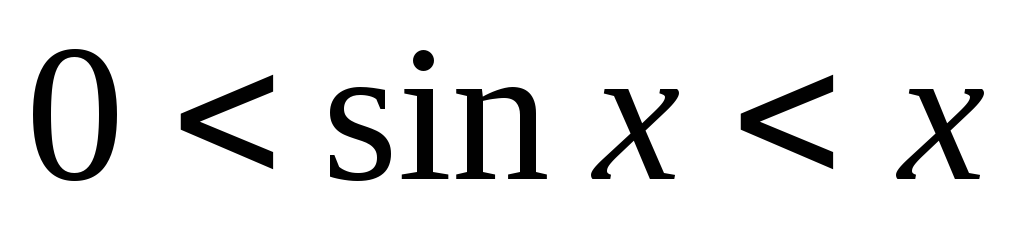
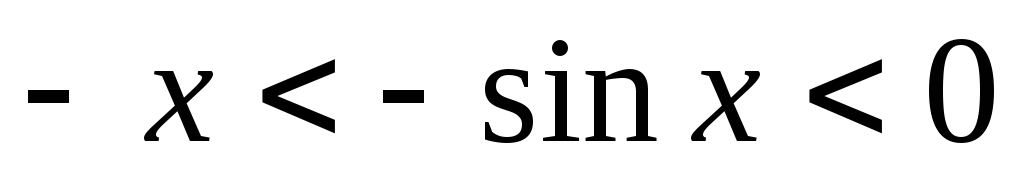
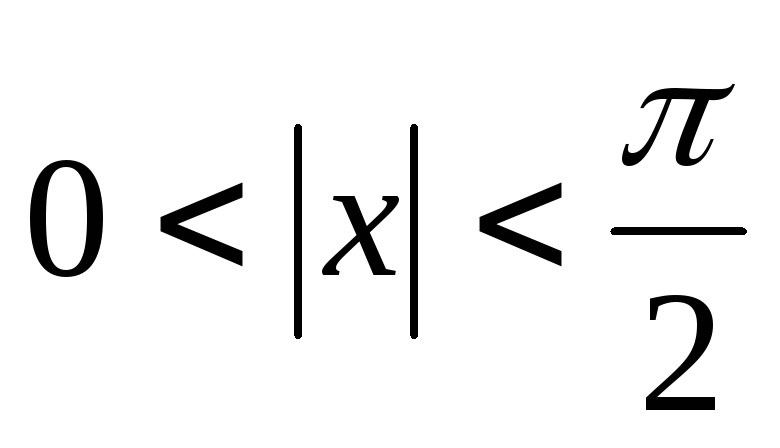
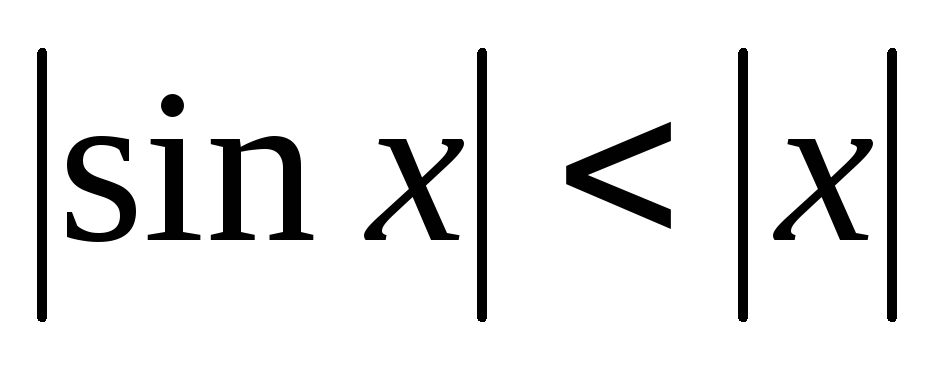
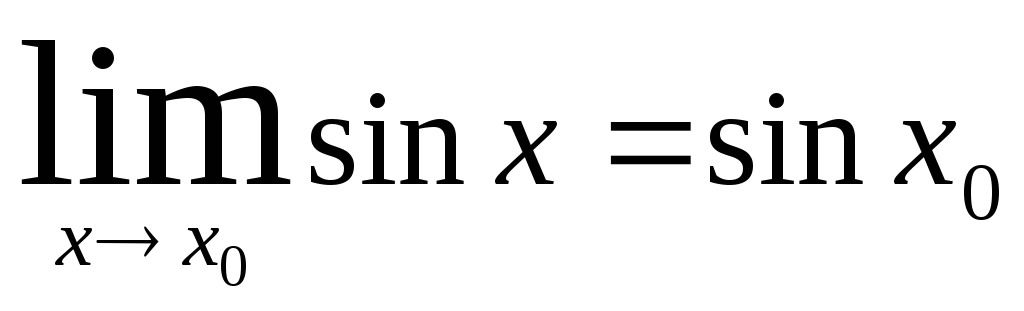
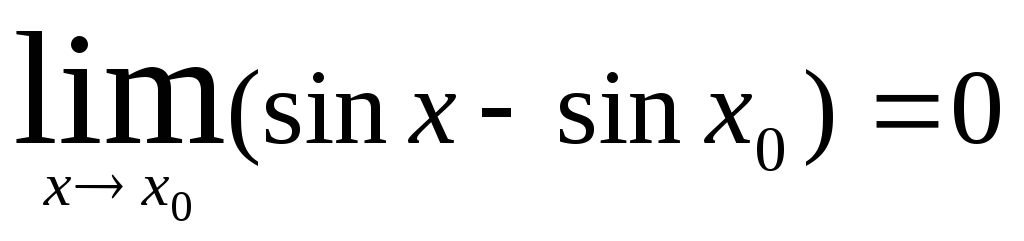
Она непрерывна по теореме о непрерывности сложной функции, так как
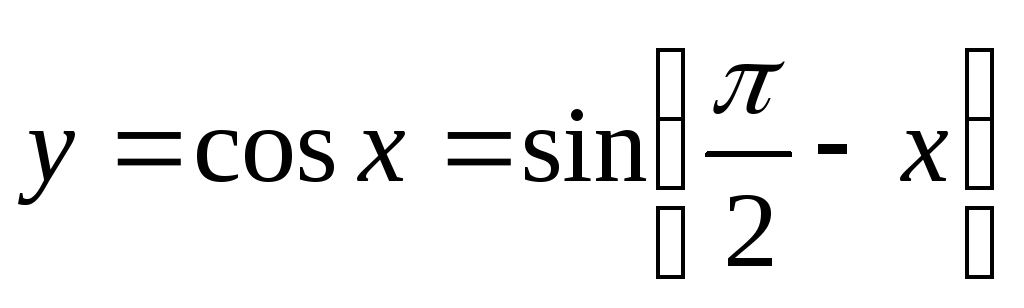
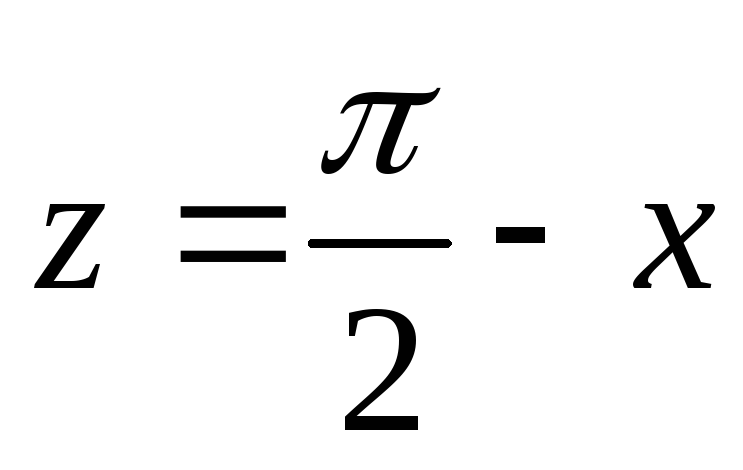
Эта функция непрерывна во всех точках, кроме 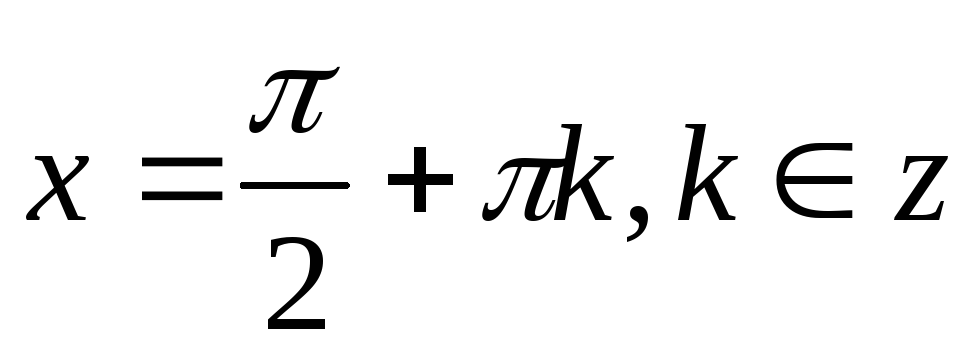
она непрерывна во всех точках, кроме точек x = n, nz, где она имеет разрыв второго рода.
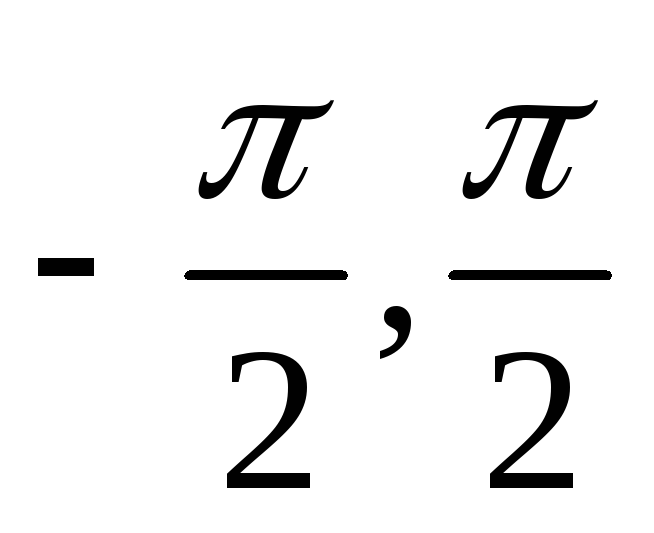
Следует из тождества arcsin x + arccos x = 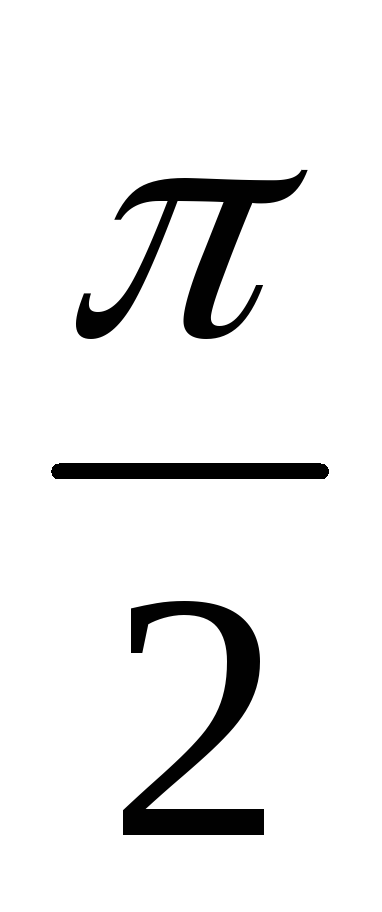
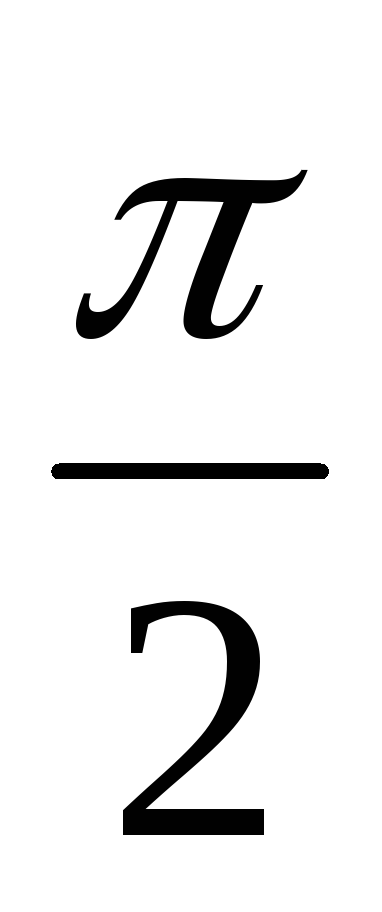
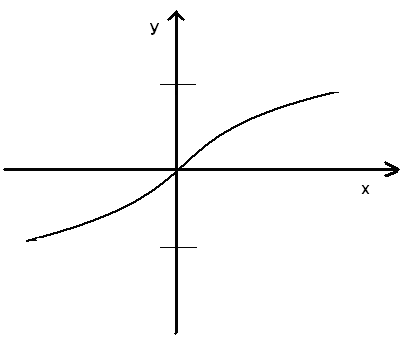
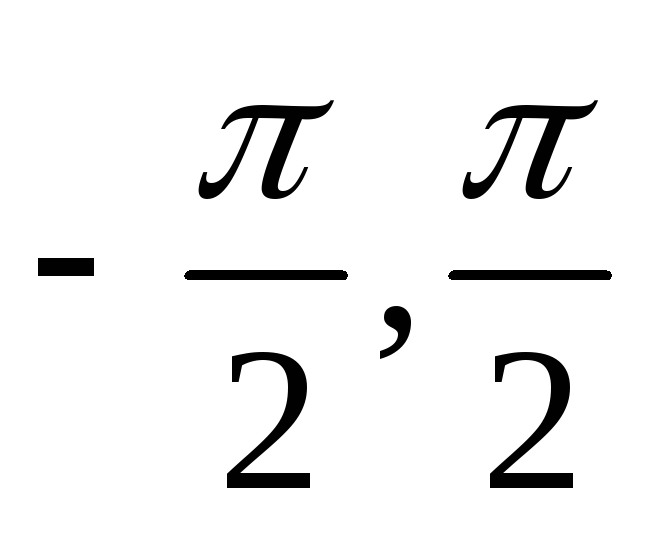
Следует из равенства : arctg x + arctg x = 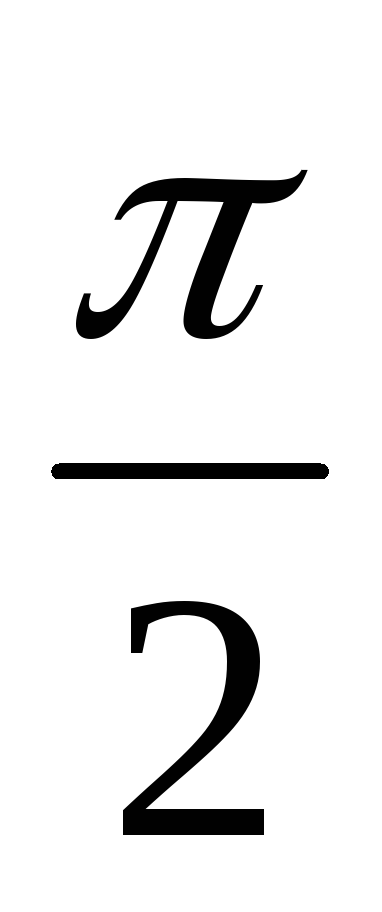
Утверждение 1
Рассмотрим многочлен степени , т. е. функцию вида
Эта функция непрерывна на
Функция где — постоянно непрерывна на так как при любом Функция непрерывна на так как при Поэтому функция где непрерывна на как произведение непрерывных функций. Так как многочлен есть сумма непрерывных функций вида то он непрерывен на
Рациональная функция, т. е. функция вида где — многочлены степени и соответственно, непрерывна во всех точках, которые не являются нулями многочлена
В самом деле, если то из непрерывности многочленов и следует непрерывность функции в точке
Утверждение 2
Рассмотрим в координатной плоскости круг единичного радиуса
с центром в точке (рис. 12.1). Пусть где .
Пусть — проекция точки на ось , луча и прямой, проведенной через точку перпендикулярно оси Тогда
Пусть — площади треугольника сектора и треугольника соответственно. Тогда
Если то 0,» title=»sin<x>>0,» /> и поэтому неравенство равносильно неравенству
откуда следует, что при выполняется неравенство Так
как и — четные функции, то неравенство справедливо и при
Следствие
Первый замечательный предел
Замечание
Из неравенства следует, что x" title="tg x>x" /> при
Утверждение 3
Для всех справедливо неравенство
Неравенство выполняется при
Если то из утверждения следует что
Если то тогда доказываемое неравенство очевидно.
Утверждение 4
Функции и непрерывны на всем множестве
Требуется доказать, что
0 exists delta_<varepsilon >:forall x:left | x-x_ <0>
ight | 0 exists delta_<varepsilon >:forall x:left | x-x_ <0>
ight |
То есть 0" title="forall varepsilon >0" />если взять
, то
Для функции доказывается аналогично
Следствие
Функция — непрерывная при
Утверждение 5
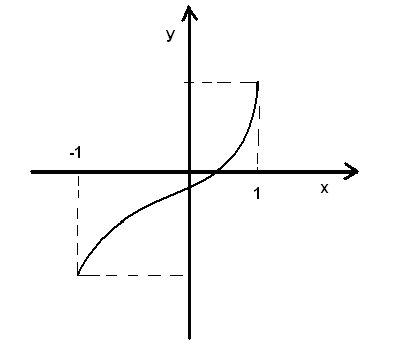
Рассмотрим несколько функции с их графиками
- строго возрастает и непрерывна
Тогда по теореме существуют обратные непрерывные монотонные функции соответственно