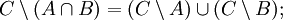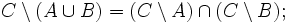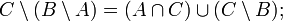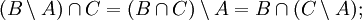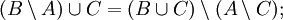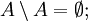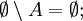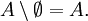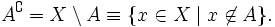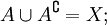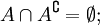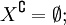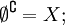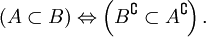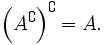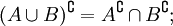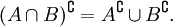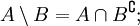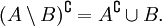varnothing ^<complement >>
mathbb setminus A>
Универса́льное мно́жество — в математике множество, содержащее все объекты и все множества. В тех аксиоматиках, в которых универсальное множество существует, оно единственно.
Универсальное множество обычно обозначается U <displaystyle mathbb > 

В аксиоматике Цермело — Френкеля парадокс Рассела со схемой выделения и парадокс Кантора показывают, что предположение о существовании такого множества ведёт к противоречию.
В аксиоматике фон Неймана — Бернайса — Гёделя существует универсальный класс — класс всех множеств, но множеством он не является. Класс всех множеств является классом объектов категории Set.
В некоторых аксиоматиках существует универсальное множество, но при этом схема выделения не выполняется. Примером является теория New Foundations [en] У. В. О. Куайна.
Также универсальным множеством называют множество объектов, рассматриваемых в каком-либо разделе математики. Для элементарной арифметики универсальным множеством является множество целых чисел, для аналитической геометрии плоскости универсальным множеством является множество всех упорядоченных пар действительных чисел [1] .
На диаграммах Венна универсальное множество (в обоих значениях) изображается множеством точек некоторого прямоугольника; подмножества его точек изображают подмножества универсального множества [1] .
В дальнейшем речь идёт о первом значении термина. Нижеприведённые формулы (за исключением U ∈ U <displaystyle mathbb in mathbb > 



Содержание
Свойства универсального множества [ править | править код ]
- Любой объект, какова бы ни была его природа, является элементом универсального множества. ∀ a : a ∈ U <displaystyle forall acolon ain mathbb >
- В частности, само универсальное множество содержит себя в качестве одного из многих элементов. U ∈ U <displaystyle mathbb in mathbb >
- Любое множество является подмножеством универсального множества. ∀ A : A ⊆ U <displaystyle forall Acolon Asubseteq mathbb >
- В частности, само универсальное множество является своим подмножеством. U ⊆ U <displaystyle mathbb subseteq mathbb >
- Объединение универсального множества с любым множеством равно универсальному множеству. ∀ A : U ∪ A = U <displaystyle forall Acolon mathbb cup A=mathbb >
- В частности, объединение универсального множества с самим собой равно универсальному множеству. U ∪ U = U <displaystyle mathbb cup mathbb =mathbb >
- Объединение любого множества с его дополнением равно универсальному множеству. A ∪ A ∁ = U <displaystyle Acup A^<complement >=mathbb >
- Пересечение универсального множества с любым множеством равно последнему множеству. ∀ A : U ∩ A = A <displaystyle forall Acolon mathbb cap A=A>
- В частности, пересечение универсального множества с самим собой равно универсальному множеству. U ∩ U = U <displaystyle mathbb cap mathbb =mathbb >
- Исключение универсального множества из любого множества равно пустому множеству. ∀ A : A ∖ U = ∅ <displaystyle forall Acolon Asetminus mathbb =varnothing >
- В частности, исключение универсального множества из себя равно пустому множеству. U ∖ U = ∅ <displaystyle mathbb setminus mathbb =varnothing >
- Исключение любого множества из универсального множества равно дополнению этого множества. ∀ A : U ∖ A = A ∁ <displaystyle forall Acolon mathbb setminus A=A^<complement >>
- Дополнение универсального множества есть пустое множество. U ∁ = ∅ <displaystyle mathbb ^<complement >=varnothing >
- Симметрическая разность универсального множества с любым множеством равна дополнению последнего множества. ∀ A : U △ A = A ∁ <displaystyle forall Acolon mathbb riangle A=A^<complement >>
- В частности, симметрическая разность универсального множества с самим собой равна пустому множеству. U △ U = ∅ <displaystyle mathbb riangle mathbb =varnothing >
Виды [ править | править код ]
- Дизъюнктивно-универсальное множество (ДУМ) G[2] порядка n и ранга p — это множество функций алгебры логики такое, что для любой g ∈ P 2 ( n ) <displaystyle gin P_<2>(n)>
существует набор функций g 1 , … , g p ∈ G <displaystyle g_<1>,ldots ,g_
in G>
такой, что:
g = g 1 ∨ … ∨ g p <displaystyle g=g_<1>lor ldots lor g_
>
Читайте также:
- Def.32 Морфизм М есть обобщение понятия бинарного соответствия между множествами на составляемые алгебраические системы.
- Def.36 Линейно упорядоченная часть упорядоченного множества М называется максимальной цепью, если оно не содержится строго ни в какой-либо другой цепи М.
- SWOT-анализ в качестве универсального метода анализа.
- Алгоритм Магу для определения множества внешней устойчивости.
- Взаимно однозначные соответствия. Понятие взаимно однозначного отображения множества Х на множество Y
- Выражения над множествами
- Вычитание
- Вычитание матриц
- Вычитание множеств. Дополнение множества
- Главные универсальные функции и множества
- Для заданного массива из N чисел построить все подмножества, определить подмножества, состоящие из простых чисел.
Лекция 3. Операции с множествами
Свойства пересечения и объединения множеств
Из школьного курса математики известно, что операция, при помощи которой находят сумму чисел, называется сложением. Над числами выполняются и другие операции, например, умножение, вычитание, деление; при этом результаты называют произведением, разностью, частным соответственно. Для операций и результатов выполнения этих операций существуют разные термины. Для рассмотренных операций над множествами и сама операция, и ее результат носят одно название.
Из школьного курса математики нам известно, что операции над числами обладают рядом свойств. Например, сложение действительных чисел обладает переместительным и сочетательным свойствами: для любых действительных чисел а и b справедливо равенство а + b = b + а, а для любых чисел а, b и с справедливо равенство (а + b) + с = а + (b + с).
Перечислим другие свойства:
а • b = b • а; (а • b) • с = а • (b • с); (а + b) • с = а • с + b • с.
Выясним, обладают ли «похожими» свойствами пересечение и объединение множеств.
Доказано, что операции над множествами обладают следующими свойствами:
1) А ∩ В = В ∩ А и А ∪ В = В ∪ А – коммутативное свойство для операций пересечения и объединения.
2) (А ∩ В) ∩ С = А ∩ (В ∩ С) и (А ∪ В) ∪ С = А ∪ (В ∪ С) ассоциативное свойство для операций пересечения и объединения.
3) (А ∪ В) ∩ С = (А ∩ С) ∪ (В ∩ С)– пересечение дистрибутивно относительно объединения множеств и
4) (А ∩ В) ∪ С = (А ∪ С) ∩ (В ∪ С) – объединение дистрибутивно относительно пересечения множеств.
Заметим, что если в выражении есть знаки пересечения и объединения множеств, и нет скобок, то сначала выполняют пересечение, так как считают, что пересечение более «сильная» операция, чем объединение.
Убедиться в справедливости сформулированных свойств можно путем доказательства, а также проиллюстрировать с помощью кругов Эйлера.
Заметим, что 1-3 свойства имеют аналоги во множестве действительных чисел, над которыми производят действия сложения и умножения. А вот аналога четвертому свойству нет. Действительно, равенство а • b + с = (а + b) •( b + с) – неверное.
Понятие пересечения и объединения множеств можно обобщить на любое конечное число множеств:
Аналогично можно поступить и по отношению к рассмотренным свойствам данных операций.
1. Вычитание множеств. Дополнение множества до универсального
2. Понятие разбиения множества на классы с помощью одного, двух, трех свойств.
3. Декартово произведение множеств
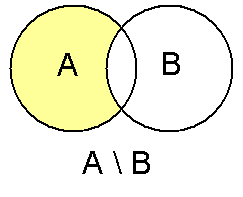
Если заданы два множества, то можно не только найти их пересечение и объединение, но и вычесть из одного множества другое. Результат вычитания называют разностьюи определяют следующим образом.
Определение. Разностью множеств А и В называют множество, содержащее все элементы, которые принадлежат множеству А и не принадлежат множеству В.
Разность множеств А и В обозначают А В. По определению: А В =<х/х∈А и х∉В>.
В школьном курсе математики чаще всего приходится выполнять вычитание множеств в случае, когда одно из них является подмножеством другого, при этом разность множеств А В называют дополнением множества В до множества А, и обозначают символом В´А, а наглядно изображают так:
Определение: Пусть В ⊂ А. Дополнением множества В до множества А называется множество, содержащее все элементы множества А, которые не принадлежат множеству В.
Выясним, как находить дополнение подмножества на конкретных примерах.
Если элементы множеств А и В перечислены и В ⊂ А, достаточно перечислить элементы, принадлежащие множеству А и не принадлежащие множеству В. Например, А = <1, 2, 3, 4, 5>, В = <2, 4>, то В´А = <1, 3, 5>.
В том случае, когда указаны характеристические свойства элементов множеств А и В и известно, что В ⊂ А, то множество В´А задают также с помощью характеристического свойства, общий вид которого «х∈А и х∉В». Так, если А – множество четных чисел, а В – множество кратных 4 чисел, то В´А — это множество, содержащее такие четные числа, которые не делятся на 4. Например, 22 ∈ В´А.
Вычитание – это третья операция над множествами. Условились считать, что пересечение – более «сильная» операция, чем вычитание. Что касается вычитания и объединения, то их считают равноправными.
Вычитание множеств обладает рядом свойств. В частности можно доказать, что для любых множеств А, В и С справедливы следующие равенства:
1) (А В) С = (А С) В);
2) (А ∪ В) С = (А С) ∪ (В С);
3) (А В) ∩ С = (А ∩ С) (В ∩ С);
4) А (В ∪ С) = (А В) ∩ (А С);
5) А (В ∩ С) = (А В) ∪ (А С).
Дата добавления: 2014-01-06 ; Просмотров: 2750 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Пусть даны два множества A и B . Тогда их (теоретико-множественная) разность определяется следующим образом:
Примеры
- Пусть
. Тогда
- Пусть
— множество всех вещественных чисел,
— множество рациональных чисел, а
— множество целых чисел. Тогда
— множество всех иррациональных чисел, а
— дробных.
Свойства
Пусть A,B,C — произвольные множества. Тогда
Компьютерные реализации
В пакете функции Complement . В пакете setdiff .
Дополнение множества
Определение
Если из контекста следует, что все рассматриваемые множества являются подмножествами некоторого фиксированного универсального множества X , то определяется операция дополнения:
Свойства
- Операция дополнения является унарной операцией на булеане 2 X .
- Законы дополнения:
В частности, если оба A и 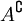
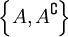
- Операция дополнения является инволюцией:
- Законы де Моргана:
- Законы разности множеств:
См. также
Wikimedia Foundation . 2010 .
Смотреть что такое "Дополнение множества" в других словарях:
Дополнение (теория множеств) — Дополнение в теории множеств это семейство элементов, не принадлежащих данному множеству. Содержание 1 Разность множеств 1.1 Определение 1.2 Примеры 1.3 Свойства … Википедия
Дополнение (математика) — Дополнение в теории множеств это семейство элементов, не принадлежащих данному множеству. Содержание 1 Разность множеств 1.1 Определение 1.2 Примеры 1.3 Свойства … Википедия
ДОПОЛНЕНИЕ — операция, к рая ставит в соответствие подмножеству Мданного множества Xдругое подмножество так, что если известны Ми N, то тем или иным способом может быть восстановлено множество X. В зависимости от того, какой структурой наделено множество X,… … Математическая энциклопедия
Дополнение графа — Граф Петерсена (слева) и его дополнение (справа). В теории графов дополнением или обратным к графу G называется такой граф H, имеющий то же множество вершин, что и G, но в котором две несовпадающие вершины смежны тогда и только тогда, когда они… … Википедия
дополнение к множеству — такое множество не А, когда A + не А = 1, где 1 обозначает некоторую предметную область (универсальный класс). Пусть A будет множеством млекопитающих, а областью нашего рассуждения будет множество позвоночных животных. Тогда дополнением к нему… … Словарь терминов логики
ДИЗЪЮНКТНОЕ ДОПОЛНЕНИЕ — множества А множество всех элементов х векторной решетки (векторной структуры) X, дизъюнктных множеству (см. Дизъюнктные элементы). кроме того, если X векторная условно полная решетка, то Add является наименьшей компонентой пространства X,… … Математическая энциклопедия
Плотные и неплотные множества — понятия множеств теории (См. Множеств теория). Множество Е называется плотным на М, если каждая точка множества М является предельной точкой (См. Предельная точка) Е, т. е. в любой окрестности имеются точки, принадлежащие Е. Плотные… … Большая советская энциклопедия
Мера множества — У этого термина существуют и другие значения, см. Мера. Мера множества неотрицательная величина, интуитивно интерпретируемая как размер (объем) множества. Собственно, мера это некоторая числовая функция, ставящая в соответствие каждому… … Википедия
КАТЕГОРИЯ МНОЖЕСТВА — топологическая характеристика массивности множества. Множество Етопологич. пространства Xназ. множеством первой категории на X, если оно представимо в виде конечной или счетной суммы множеств, нигде не плотных на X. В противном случае Еназ.… … Математическая энциклопедия
Существование перечислимого неразрешимого множества — В данной статье будет доказан теорема о существовании перечислимого, но неразрешимого множества. Напомню, что по теореме Поста перечислимое множества разрешимо тогда и только тогда, когда его дополнение перечислимо.Основные определения, такие как … Википедия






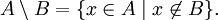
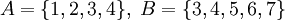 . Тогда
. Тогда 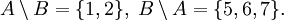
 — множество всех вещественных чисел,
— множество всех вещественных чисел, 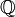 — множество рациональных чисел, а
— множество рациональных чисел, а  — множество целых чисел. Тогда
— множество целых чисел. Тогда 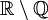 — множество всех иррациональных чисел, а
— множество всех иррациональных чисел, а 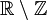 — дробных.
— дробных.