Необходимый признак сходимости ряда.
Числовые ряды.
Определение:
Пусть a1,a2. an. — бесконечная числовая последовательность. Выражение вида: a1+a2+. +an+. =(n=1)∑ ∞ an называется числовым рядом. При этом числа a1,a2. an. называются членами ряда. А число an — n-ым, или общим, членом ряда.
Ряд считается заданным, если известен закон образования его n-го члена.
Определение:
Сумма конечного числа первых n членов ряда (n=1)∑ ∞ an называется n-ой частичной суммой этого ряда и обозначается: Sn=a1+a2+a3+. +an
Определение:
Если для последовательности частичных сумм Sn числового ряда существует конечный предел, т.е. lim Sn=S ∞ an называется сходящимся, а число S — является суммой этого ряда. Если предел Sn не существует (или равен бесконечности), то ряд называется расходящимся.
На сходимость и расходимость ряда не влияет отбрасывание любого конечного числа его членов.
Теорема:
Если ряд (n=1)∑ ∞ an сходится, то lim an=0.
Относительно практики эта теорема является достаточным условием расходимости числового ряда, т.е. если lim an≠0, то (n=1)∑ ∞ an — расходится.
Положительного вывода о сходимости из одного необходимого признака никогда сделать нельзя.
I. Признак сравнения.
Пусть заданы два ряда:
a1+a2+. +an+. =(n=1)∑ ∞ an
b1+b2+. +bn+. =(n=1)∑ ∞ bn
Если для любого i выполняется ai≥bi, то ряд (n=1)∑ ∞ an называется мажорантным по отношению к ряду (n=1)∑ ∞ bn, а ряд (n=1)∑ ∞ bn — минорантным по отношению к (n=1)∑ ∞ an.
Теорема(1):
Если мажорантный ряд сходится, то и минорантный ряд также сходится.
Теорема(2) (достаточный признак расходимости):
Если минорантный ряд расходится, то и мажорантный к нему ряд также расходится.
Замечание:
Признак сравнения даёт ответ только в двух случаях из четырёх возможных при работе с двумя рядами.
Чтобы сравнивать ряды необходимо иметь такие ряды для сравнения, про которые заранее известно о их сходимости или расходимости. К самым популярным из них относятся:
1. Ряды, составленные из членов геометрической прогрессии, про которые известно, что при |q| ∞ 1/n α ), которые сходятся при α>1 и расходятся при α≤1.
Особо стоит отметить гармонический ряд при α=1, который является расходящимся!
II. Признак д’Аламбера.
Теорема:
Если в ряде с положительными членами отношение (n+1)-го члена (аn+1) к an при n→∞ имеет конечный предел, т.е. lim (аn+1/аn)=l 1 — ряд расходится;
3) l=1 — результат не определён.
III. Интегральный признак Коши
Если члены знакоположительного ряда не возрастают, то вопрос о сходимости или расходимости ряда может быть решён с помощью так называемой "производной функции", где f(1)=a1, f(2)=a2, . f(n)=an. При этом, если 1∫ +∞ f(x)dx — сходится, то ряд также сходится, а если 1∫ +∞ f(x)dx — расходится, то и ряд — расходится.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент — человек, постоянно откладывающий неизбежность. 10580 — 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Перед началом работы с этой темой советую посмотреть раздел с терминологией для числовых рядов. Особенно стоит обратить внимание на понятие общего члена ряда. Если у вас есть сомнения в правильности выбора признака сходимости, советую глянуть тему "Выбор признака сходимости числовых рядов".
Необходимый признак сходимости числовых рядов имеет простую формулировку: общий член сходящегося ряда стремится к нулю. Можно записать этот признак и более формально:
Часто в литературе вместо словосочетания "необходимый признак сходимости" пишут "необходимое условие сходимости". Однако перейдём к сути: что означает данный признак? А означает он следующее: если $lim_u_n=0$, то ряд может сходиться. Если же $lim_u_n
eq 0$ (или же предела попросту не существует), то ряд $sumlimits_^<infty>u_n$ расходится.
Стоит обратить внимание, что равенство $lim_u_n=0$ вовсе не означает сходимости ряда. Ряд может как сходиться, так и расходиться. А вот если $lim_u_n
eq 0$, то ряд гарантированно расходится. Если эти нюансы требуют детальных пояснений, то прошу раскрыть примечание.
Что означает словосочетание "необходимое условие"? показатьскрыть
Поясним понятие необходимого условия на примере. Для покупки ручки студенту необходимо иметь 10 рублей. Это можно записать так: если студент покупает ручку, то у него есть 10 рублей. Наличие десяти рублей – это и есть необходимое условие покупки ручки.
Пусть это условие выполнено, т.е. десятка у студента есть. Значит ли это, что он купит ручку? Вовсе нет. Он может купить ручку, а может приберечь деньги на потом. Или купить что-либо иное. Или подарить их кому-то, – вариантов масса 🙂 Иными словами, выполнение необходимого условия покупки ручки (т.е. наличие денег) вовсе не гарантирует покупку этой ручки.
Точно так же и необходимое условие сходимости числового ряда $lim_u_n=0$ вовсе не гарантирует сходимость этого самого ряда. Простая аналогия: если есть деньги, студент может купить ручку, а может и не купить. Если $lim_u_n=0$, ряд может как сходиться, так и расходиться.
Однако что произойдет, если необходимое условие покупки ручки не выполнено, т.е. денег нет? Тогда студент ручку точно не купит. То же самое и с рядами: если необходимое условие сходимости не выполнено, т.е. $lim_u_n
eq 0$, то ряд точно будет расходиться.
Говоря кратко: если необходимое условие выполнено, то следствие может как произойти, так и не произойти. Однако если необходимое условие не выполнено, то следствие точно не произойдёт.
Для наглядности приведу пример двух рядов: $sumlimits_^<infty>frac<1>
Однако гармонический ряд $sumlimits_^<infty>frac<1>
Исходя из необходимого условия сходимости ряда можно сформулировать достаточный признак расходимости числового ряда:
Чаще всего в стандартных примерах необходимый признак сходимости проверяется, если общий член ряда представлен дробью, числитель и знаменатель которой есть некие многочлены. Например, $u_n=frac<3n^2+2n-1><5n^2+7>$ (см. пример №1). Или же могут присутствовать корни от многочленов (см. пример №2). Бывают примеры, которые несколько выбиваются из данной схемы, но для стандартных контрольных работ это редкость (см. примеры во второй части этой темы). Подчеркну главное: с помощью необходимого признака нельзя доказать сходимость ряда. Этот признак используют, когда нужно доказать, что ряд расходится.
Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=frac<3n^2+2n-1><5n^2+7>$. Найдём предел общего члена ряда:
Если метод решения данного предела вызывает вопросы, то советую обратиться к теме "Предел отношения двух многочленов". Так как предел общего члена ряда не равен нулю, т.е. $lim_u_n=frac<3><5>
eq 0$, то необходимый признак сходимости не выполнен. Следовательно, ряд расходится.
Решение окончено, однако, полагаю, у читателя возникнет вполне резоннный вопрос: а как мы вообще увидели, что нужно проверить выполнение необходимого условия сходимости? Существует немало признаков сходимости числовых рядов, так почему же взяли именно этот? Данный вопрос совсем не праздный. Но так как ответ на него, возможно, будет интересен не всем читателям, то я скрыл его под примечание.
Почему мы начали применять именно необходимый признак сходимости? показатьскрыть
Если говорить нестрого, то вопрос сходимости этого ряда решается ещё до формального исследования. Я не буду касаться такой темы как порядок роста, просто приведу некие общие рассуждения. Давайте посмотрим на общий член ряда $u_n=frac<3n^2+2n-1><5n^2+7>$ повнимательнее. Сначала обратимся к числителю. Число (-1), расположенное в числителе, можно отбросить сразу: если $n oinfty$, то данное число будет пренебрежимо малым по сравнению с остальными слагаемыми.
Посмотрим на степени $n^2$ и $n$, имеющиеся в числителе. Вопрос: какой элемент ($n^2$ или $n$) будет расти быстрее прочих?
Ответ здесь прост: наиболее быстро будет увеличивать свои значения именно $n^2$. Например, когда $n=100$, то $n^2=10;000$. И этот разрыв между $n$ и $n^2$ будет всё больше и больше. Поэтому все слагаемые, кроме тех, что содержат $n^2$, мы мысленно отбросим. После такого "отбрасывания" в числителе останется $3n^2$. А после проведения подобной процедуры для знаменателя, там останется $5n^2$. И дробь $frac<3n^2+2n-1><5n^2+7>$ теперь станет такой: $frac<3n^2><5n^2>=frac<3><5>$. Т.е. на бесконечности общий член явно не будет стремиться к нулю. Осталось лишь показать это формально, что и было сделано выше.
Частенько в записи общего члена ряда используют такие элементы, как, например, $sinalpha$ или $arctgalpha$ и тому подобное. Нужно просто помнить, что значения подобных величин не могут выходить за некие числовые границы. Например, каким бы ни было значение $alpha$, значение $sinalpha$ останется в пределах $-1≤sinalpha≤ 1$. Т.е., к примеру, мы можем записать, что $-1≤sin(n!e^n)≤ 1$. А теперь представьте, что в записи общего члена ряда расположено выражение вроде $5n+sin(n!e^n)$. Сыграет ли синус, который может "колебаться" лишь от -1 до 1, хоть какую-либо значимую роль? Ведь значения $n$ устремляются в бесконечность, а синус не сможет превысить даже единицу! Поэтому при предварительном рассмотрении выражения $5n+sin(n!e^n)$ синус можно просто отбросить.
Или, для примера, возьмём арктангенс. Каким бы ни было значение аргумента $alpha$, значения $arctgalpha$ будут удовлетворять неравенству $-frac<pi> <2>of your page —>
Раздел 7. Числовые и степенные ряды
Числовые ряды
Основные определения
Определение. Пусть 
называется числовым рядом. Числа 
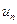
Определение. Суммы 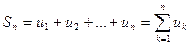

Определение. Ряд 
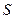


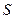
Определение. Если последовательность частичных сумм 


Свойства числовых рядов
1) Сходимость или расходимость ряда не нарушится, если отбросить или добавить произвольное конечное число членов ряда.
2) Рассмотрим два ряда 
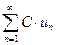
Теорема. Если ряд 


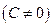
3) Рассмотрим два ряда 

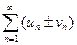
Теорема. Если ряды 



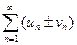

Сумма (разность) двух сходящихся рядов также является сходящимся рядом.
Сумма сходящегося и расходящегося рядов является расходящимся рядом.
О сумме двух расходящихся рядов общего утверждения сделать нельзя.
При изучении рядов решают в основном две задачи: исследование на сходимость и нахождение суммы ряда.
Необходимые и достаточные условия сходимости числовых рядов
Теорема.(Критерий Коши) Для того, чтобы последовательность 
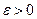

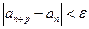
Доказательство. (необходимость) Пусть 
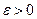



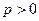

Необходимость доказана. Доказательство достаточности рассматривать не будем.
Сформулируем критерий Коши для ряда.
Для того чтобы ряд 
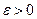

Однако на практике использовать непосредственно критерий Коши не очень удобно, поэтому, как правило, используются более простые признаки сходимости.
Теорема.(Необходимый признак сходимости ряда). Если ряд 
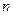

Это условие не является достаточным. Однако, если общий член ряда не стремится к нулю, то ряд расходится. Например, так называемый гармонический ряд 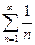
Пример. Исследовать сходимость ряда
Найдем 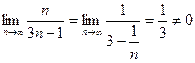
Теорема.Если ряд сходится, то последовательность его частичных сумм ограничена.
Это условие не является достаточным.
Например, ряд 
Однако при этом последовательность частичных сумм ограничена, т.к. 







