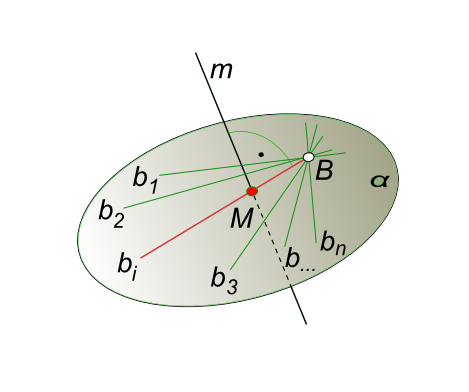
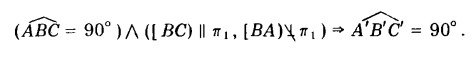Взаимно перпендикулярные прямые — это прямые пересекающиеся под прямым углом. Построить взаимно перпендикулярные прямые бывает необходимо для решения той или иной задачи. Например в задаче на определение расстояния от точки до прямой. Наглядное пространственное представление графического решения задачи на построение взаимно перпендикулярных прямых дает рисунок

Через точку B можно провести множество прямых , перпендикулярных к прямой m. Это множество прямых определяет плоскость α ⊥ m.
Чтобы выделить из единственную прямую bi, пересекающую данную прямую m и следовательно взаимно перпендикулярную к ней, необходимо:
— Найти точку встречи прямой m с плоскостью α. M = m ∩ α;
— Зная положение точки M, провести через нее прямую bi и определить действительную величину отрезка [BM], выражающую искомое расстояние от точки до прямой.
На основе выше приведенного рисунка может быть решена задачи по построению перпендикулярных прямых которые не пересекаются, трех взаимно перпендикулярных прямых.

Прямой угол между двумя пересекающимися прямыми проецируется без искажения, если хотя бы одна из прямых параллельна плоскости проекций.
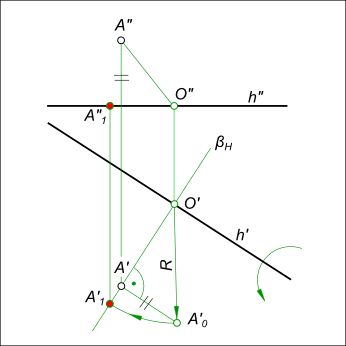
Найти расстояние от точки A до прямой h. Решение подобной задачи предполагает, что будут построены взаимно перпендикулярные прямые

Для определения натуральной величины отрезка перпендикуляра от точки A до прямой h используем способ вращения вокруг горизонтали: — через точку A проводим горизонтально проецирующую плоскость βH ⊥ h` и на их пересечении находим O` и по линии связи O" — проекции центра вращения; — определяем действительную величину радиуса вращения R=[O`A`0], применив способ прямоугольного треугольника; — описываем дугу радиуса R до пересечения с βH и находим точку A`1 и расстояние от точки A до прямой h в виде отрезка [A`1O`] ⊥ h`. [AO] ⊥ h — это прямые пересекающиеся под прямым углом — взаимно перпендикулярные прямые.

Для того чтобы построить взаимно перпендикулярные прямые, в случае когда одна из них задана прямой общего положения, необходимо перевести ее, предварительно, в положение либо горизонтали, либо фронтали

Здесь построение второй стороны прямого угла выполняется способом перемены плоскости проекции. Вводится новая фронтальная плоскость проекции V1, для которой сторона AB прямого угла есть фронтальная прямая. И тогда прямой угол ABC проецируется на V1 без искажения. Аппликата точки C при перемене плоскости V на V1 остается неизменной и ее пресечение с направлением стороны BC дает положение искомой точки C1. Искомую проекцию C` находим на пересечении линий связи точки C.

Та же задача на взаимно перпендикулярные прямые может быть решена по другим способом

Здесь сторона BC, заключается в плоскость перпендикулярную второй стороне прямого угла AB. Затем в этой плоскости проводится прямая 1 — 2 через точку C и находится горизонтальная проекция C`, как принадлежащая прямой 1` — 2`.

Не будет преувеличением утверждать, что построение взаимно перпендикулярных прямых и плоскостей наряду с определением расстояния между двумя точками являются основными графическими операциями при решении метрических задач.

Теоретической предпосылкой для построения на эпюре Монжа проекций прямых и плоскостей, перпендикулярных по отношению друг к другу в пространстве, служит отмеченное раньше (см. § 6) свойство

проекции прямого угла, одна из сторон которого параллельна какой-либо плоскости проекции:

1. Взаимно перпендикулярные прямые.

Чтобы можно было воспользоваться отмеченным свойством для построения на эпюре Монжа двух пересекающихся под углом 90° прямых, необходимо, чтобы одна из них была параллельна какой-либо плоскости проекции. Поясним сказанное на примерах.

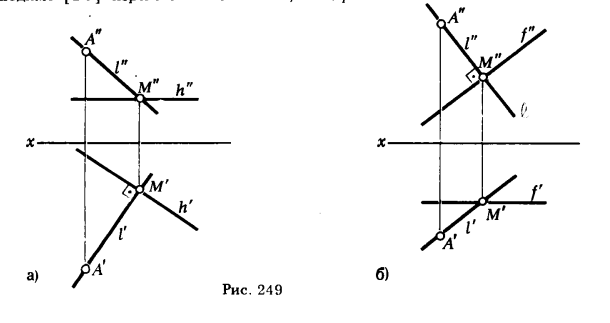
ПРИМЕР 1. Через точку А провести прямую l, пересекающую горизонталь h под прямым углом (рис. 249).

Так как одна из сторон h прямого угла параллельна плоскости π1 , то на эту плоскость прямой угол спроецируется без искажения. Поэтому через А’ проводим горизонтальную проекцию l’ ⊥ h’. Отмечаем точку М’ = l’ ∩ h’. Находим М" (М" ∈ h"). Точки А" и М" определяют l" (см. рис. 249, а).

Если вместо горизонтали будет задана фронталь f, то геометрические построения по проведению прямой l ⊥ f аналогичны только что рассмотренным с той лишь разницей, что построения неискаженной проекции прямого угла следует начинать с фронтальной проекции (см. рис. 249, б).

ПРИМЕР 2. Через точку А провести прямую l , пересекающую прямую а , заданную отрезком [ВС], под углом 90° (рис. 250).

Так как данный отрезок занимает произвольное положение по отношению к плоскостям проекций, мы не можем, как в предыдущем примере, воспользоваться свойством о частном случае проецирования прямого угла, поэтому вначале необходимо [ВС] перевести в положение, параллельное какой-либо плоскости проекции.

На рис. 250 [ВС] переведен в положение, параллельное плоскости π3. Это сделано с помощью способа замены плоскостей проекции путем замены плоскости π1 → π3 || [ВС].

В результате такой замены в новой системе x1π2/π3 [ВС] определяет горизонтальную прямую, поэтому все дальнейшие простроения выполнены так же, как это было сделано в предыдущем примере: после того, как была найдена точка М’1, ее перевели на исходные плоскости проекции в положение М" и М’, эти точки совместно с А" и А’ определяют проекции прямой l.

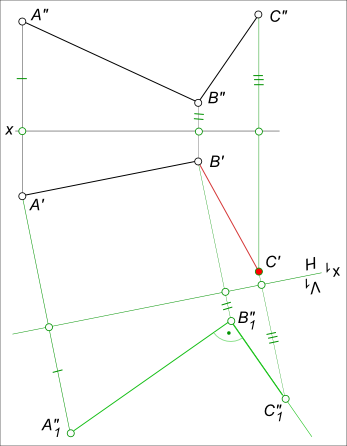
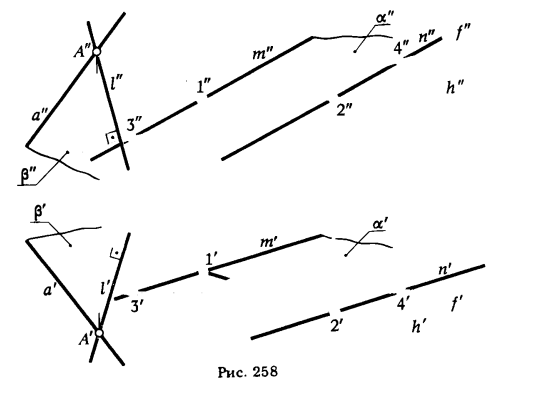
ПРИМЕР 3. Провести горизонтальную проекцию стороны [ВС] прямого угла АВС, если известны его фронтальная проекция ∠A"B"C" и горйзонтапьная проекция стороны [А’В’] (рис. 251).

1. Переводим сторону угла [ВА] в положение || π3 путем перехода от системы плоскостей проекции хπ2/π1 к новой x1π3/π2

2. Определяем новую фронтальную проекцию [B"1A"1].

Из В"1 восставляем перпендикуляр к [В"1A"1]. На этом перпендикуляре определяем точку С"1 (С"1 удалена от оси x1 на расстояние |Сx1 С"1| = |СxС"|).

4. Горизонтальная проекция С’ определяется как точка пересечения прямых (С"1Сx1) ∩ (С"Сx) = С’.

2. Взаимно перпендикулярные прямая и плоскость.

Из курса стереометрии известно, что прямая перпендикулярна плоскости, если она перпендикулярна хотя бы к двум пересекающимся прямым, принадлежащим этой плоскости.

Если в плоскости взять не произвольные пересекающиеся прямые, а ее горизонталь и фронталь, то открывается возможность воспользоваться свойством проекции прямого угла, как это было сделано в примере 1, рис. 249.

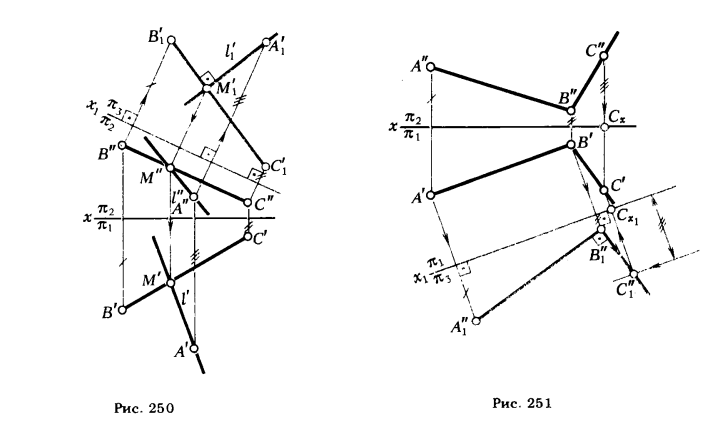
Рассмотрим следующий пример; пусть из точки A ∈ α требуется восставить перпендикуляр к плоскости α (рис. 252).

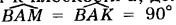
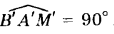
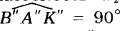
Через точку А проводим горизонталь h и фронталь f плоскости α. Тогда, по определению (АВ), перпендикулярная к плоскости α, должна быть перпендикулярна к прямым h и f, т. е. . Но сторона AM ∠ ВАМ || π1, поэтому ∠ВАМ проецируется на плоскость π1, без искажения, т. е.. Сторона АК ∠ ВАК || π2 и, следовательно, на плоскость π2 этот угол проецируется также без искажения, т. е. и . Приведенные рассуждения можно сформулировать в виде следующей теоремы: для того чтобы прямая в пространстве была перпендикулярна плоскости, необходимо и достаточно, чтобы на эпюре горизонтальная проекция прямой была перпендикулярна к горизонтальной проекции горизонтали плоскости, а фронтальная проекция к фронтальной проекции фронтали этой плоскости.

Если плоскость задана следами, то теорема может быть сформулирована иначе: для того чтобы прямая в пространстве была перпендикулярна плоскости, необходимо и достаточно, чтобы проекции этой прямой были перпендикулярны к одноименным следам плоскости.

Установленные теоремой зависимости между прямой в пространстве, перпендикулярной к плоскости, и проекциями этой прямой к проекциям линий уровня (следам) плоскости лежат в основе графического алгоритма решения задачи по проведению прямой, перпендикулярной к плоскости, а также построения плоскости, перпендикулярной к заданной прямой.

ПРИМЕР 1. Восставить в вершине А перпендикуляр AD к плоскости ΔАВС (рис. 253).

Для того чтобы определить направление проекций перпендикуляра, проводим проекции горизонтали h и фронтали f плоскости ΔАВС. После этого из точки А’ восставляем перпендикуляр к h’, а из А" — к f’.

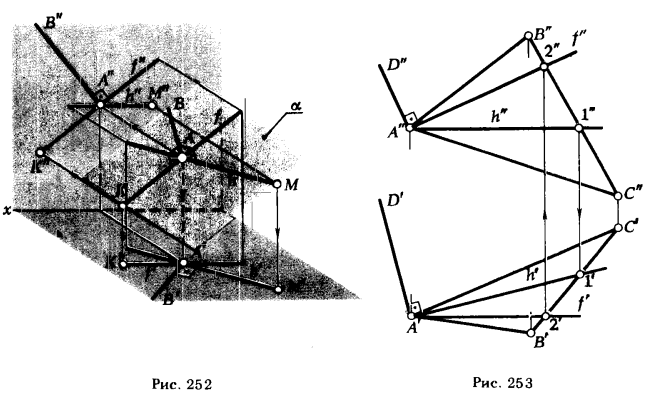
ПРИМЕР 2. Из точки А, принадлежащей плоскости α (m || n), восставить перпендикуляр к этой плоскости (рис. 254).

РЕШЕНИЕ. Для определения направления проекций перпендикуляра l’ и l", как и в предыдущем примере, проводим через точку А (А’,А") горизонталь h(h’, h"), принадлежащую плоскости α. Зная направление h’, строим горизонтальную проекцию перпендикуляра l’ (l’ ⊥ h’). Для определения направления фронтальной проекции перпендикуляра через точку А (А’, А") проводим фронталь f (f’, f") плоскости α. В силу параллельности f фронтальной плоскости проекции прямой угол между l и f проецируется на π2 без искажения, поэтому проводим l" ⊥ f".

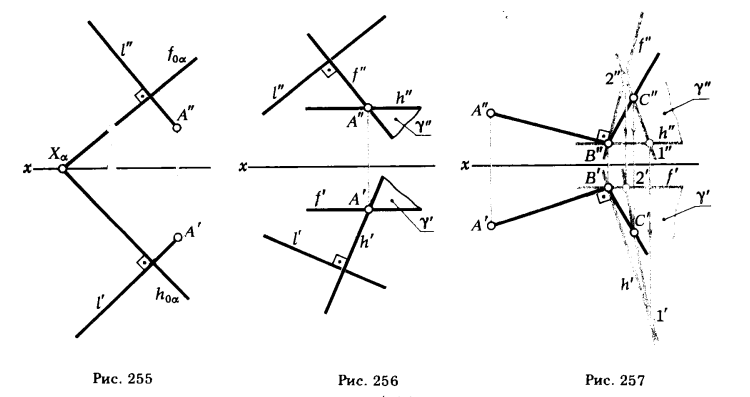
На рис. 255 эта же задача решена для случая, когда плоскость α задана следами. Для определения направлений проекций перпендикуляра отпадает необходимость в проведении горизонтали и фрон-

тали, так как их функции выполняют следы плоскости h0α и f0α. Как видно из чертежа, решение сводится к проведению через точки А’ и А" проекций l’ ⊥ h0α и l" ⊥ f0α.

ПРИМЕР 3. Построить плоскость γ, перпендикулярную к данной прямой l и проходящую через заданную точку А (рис. 256).

РЕШЕНИЕ. Через точку А проводим горизонталь h и фронталь f. Эти две пересекающиеся прямые определяют плоскость; чтобы она была перпендикулярна к прямой l, необходимо, чтобы прямые h и f составляли с прямой l угол 90°. Для этого проводим h’ ⊥ l’ и f" ⊥ l". Фронтальная проекция h" и горизонтальная проекция f’ проводятся параллельно оси x.

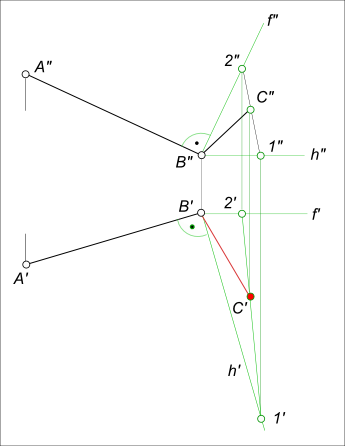
Рассмотренный случай позволяет по иному решать задачу, приведенную в примере 3 (с. 175 рис. 251). Сторона [ВС] ∠АВС должна принадлежать плоскости γ ⊥ [АВ] и проходить через точку В (рис. 257).

Это условие и определяет ход решения задачи, который состоит в следующем: заключаем точку В в плоскость γ ⊥ [АВ], для этого через точку В проводим горизонталь и фронталь плоскости γ так, чтобы h’ ⊥ A’B’ и f" ⊥ A"B".

Точка С ∈ (ВС), принадлежащей плоскости γ, поэтому для нахождения ее горизонтальной проекции проводим через С" произвольную прямую 1"2", принадлежащую плоскости γ; определяем горизонтальную проекцию этой прямой 1’2′ и на ней отмечаем точку С’ (С’ определяется пересечением линии связи — перпендикуляра, опущенного из С", с горизонтальной проекцией прямой 1’2′). С’ совместно с В’ определяют горизонтальную проекцию (ВС) ⊥ (АВ).

3. Взаимно перпендикулярные плоскости..

Две плоскости перпендикулярны, если одна из них содержит прямую, перпендикулярную к другой плоскости.

Исходя из определения перпендикулярности плоскостей, задачу на построение плоскости β, перпендикулярной к плоскости α, решаем следующим путем: проводим прямую l, перпендикулярную к плоскости α; заключаем прямую l в плоскость β. Плоскость β ⊥ α, так как β ⊃ l ⊥ α.

Через прямую l можно провести множество плоскостей, поэтому задача имеет множество решений. Чтобы конкретизировать ответ, необходимо указать дополнительные условия.

ПРИМЕР 1. Через данную прямую а провести плоскость β, перпендикулярную к плоскости α (рис. 258).

РЕШЕНИЕ. Определяем направление проекций перпендикуляра к плоскости α, для этого находим горизонтальную проекцию горизонтали (h’) и фронтальную проекцию фронтали (f") ; из проекций произвольной точки А ∈ α проводим проекции перпендикуляра l’ ⊥ h’ и l" ⊥ f". Плоскость β ⊥ α, так как β ⊃ l ⊥ α.

ПРИМЕР 2. Через данную точку А провести горизонтально проецирующую плоскость γ, перпендикулярную к плоскости α, заданной следами (рис. 259, а).

Искомая плоскость γ должна содержать прямую, перпендикулярную плоскости α, или быть перпендикулярной к прямой, принадлежащей плоскости α. Так как плоскость γ должна быть горизонтально проецирующей, то прямая, перпендикулярная к ней, должна быть параллельна плоскости π1, т. е. являться горизонталью плоскости α или (что то же самое) горизонтальным следом этой плоскости — h0α Поэтому через горизок тальную проекцию точки А’ проводим горизонтальный след h0γ ⊥ h0α фронтальный след f0γ ⊥ оси х.

На рис. 259, б показана фронтально проецирующая плоскость γ, проходящая через точку В и перпендикулярная к плоскости π2.

Из чертежа видно, что отличительной особенностью эпюра, на котором заданы две взаимно перпендикулярные плоскости, из которых одна — фронтально проецирующая, является перпендикулярность их фронтальных следов f0γ ⊥ f0α, горизонтальный след фронтально проецирующей плоскости перпендикулярен оси х.

Читайте также:

  1. Взаимно перпендикулярные плоскости.
  2. Взаимно перпендикулярные прямые
  3. Взаимно-перпендикулярные плоскости
  4. ВЗАИМНОЕ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ
  5. Взаимное положение двух прямых
  6. Взаимное положение отрезков прямых
  7. Взаимное положение плоскостей
  8. Взаимное положение плоскостей и угол между ними
  9. Взаимное положение прямой и плоскости
  10. Взаимное положение прямых
  11. Взаимное положение прямых

В связи с тем, что прямой угол между прямыми общего положения искажается на обеих плоскостях проекций, задачу на построение взаимно перпендикулярных прямых общего положения приходится сводить к задаче о перпендикулярности прямой и плоскости. При этом исходят из того, что две прямые взаимно перпендикулярны в том и только в том случае, если через каждую из них можно провести плоскость перпендикулярную к другой прямой.

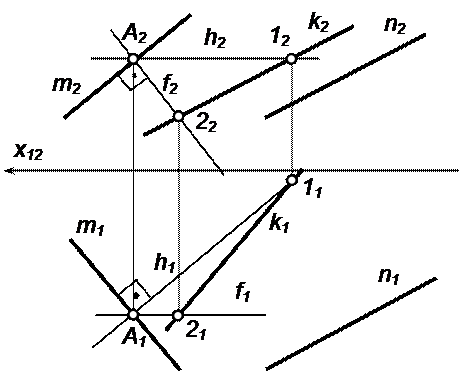
Рассмотрим пример. Через точку А провести прямую n, перпендикулярную прямой m (рис.5.12).

Сначала через точку А проведём плоскость Σ, перпендикулярную заданной прямой m. Эту плоскость зададим горизонталью и фронталью, каждая из которых перпендикулярна к прямой m (горизонтальная проекция горизонтали h1┴m1, фронтальная проекция фронтали f2┴m2). Затем нужно найти точку пересечения построенной плоскости с прямой m. Для этого прямую m заключаем во фронтально проецирующую плоскость Θ (фронтальная проекция плоскости Θ2 совпадает с фронтальной проекцией прямой m2). Далее определяем прямую 12 пересечения плоскостей Σ и Θ. После этого находим точку 3 пересечения прямой m с плоскостью Σ. Через эту точку и точку А проходит искомая прямая n.

Иногда приходится отвечать на вопрос: перпендикулярны ли между собой две заданные прямые? Для ответа на этот вопрос необходимо выполнить следующие действия:

1) построить вспомогательную плоскость, перпендикулярную одной из заданных прямых;

2) определить взаимное положение второй прямой и вспомогательной плоскости. Если вторая прямая будет принадлежать вспомогательной плоскости или ей параллельна, то заданные прямые перпендикулярны друг другу. В противном случае прямые не перпендикулярны.

Рассмотрим пример. Определить, перпендикулярны ли между собой прямые n и m (рис.5.13).

Через произвольную точку А прямой m проводим плоскость Θ, перпендикулярную прямой n. Эту плоскость зададим горизонталью и фронталью, каждая из которых перпендикулярна к прямой n. Затем в плоскости Θ строим прямую 12, так, чтобы, например, фронтальная проекция 1222 была бы параллельна фронтальной проекции n2 прямой n. Теперь если горизонтальные проекции прямых 1121 и n1 окажутся параллельными, то прямая n будет параллельна плоскости Θ и, следовательно, будет перпендикулярна к прямой m. Однако в случае, приведённом на рис.5.13 проекции прямых 1121 и n1 не параллельны. А это значит, что заданные прямые m и n не перпендикулярны друг другу.

Дата добавления: 2014-01-07 ; Просмотров: 405 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет