Движе́ние — преобразование метрического пространства, сохраняющее расстояние между соответствующими точками, то есть если A ′ <displaystyle A’> 




Несмотря на то, что движение определяется на всех метрических пространствах, этот термин более распространён в евклидовой геометрии и смежных областях. В метрической геометрии (в частности, в римановой геометрии) чаще говорят: изометрия пространства в себя. В общем случае метрического пространства (например, для неплоского риманова многообразия) движения могут существовать далеко не всегда.
Иногда под движением понимают преобразование Евклидова пространства, сохраняющее ориентацию. В частности, осевая симметрия плоскости движением не считается, а поворот и параллельный перенос считаются движением. Аналогично для общих метрических пространств движением считается элемент группы изометрий из связной компоненты тождественного отображения.
В евклидовом (или псевдоевклидовом) пространстве движение автоматически сохраняет также углы, так что сохраняются все скалярные произведения.
Далее в этой статье рассматриваются изометрии только евклидова точечного пространства.
Содержание
Собственные и несобственные движения [ править | править код ]
Пусть f : E → E <displaystyle fcolon E
ightarrow E> 



ightarrow V,> 





Собственные движения сохраняют ориентацию пространства E , <displaystyle E,> 
Всякое движение n-мерного евклидова точечного пространства E <displaystyle E> 




В механике в понятие «движение» вкладывается другой смысл; в частности, оно всегда рассматривается как непрерывный процесс, происходящий в течение некоторого промежутка времени (см. механическое движение). Если, следуя П. С. Александрову, называть непрерывным движением такое движение пространства E , <displaystyle E,> 




Частные виды изометрий [ править | править код ]
На прямой [ править | править код ]
Любое движение прямой есть либо параллельный перенос (сводящийся к смещению всех точек прямой на один и тот же вектор, лежащий на этой же прямой), либо отражение относительно некоторой точки, взятой на данной прямой. В первом случае движение является собственным, во втором — несобственным [6] .
На плоскости [ править | править код ]
Любое движение плоскости относится к одному из следующих типов [2] :
Движения первых двух типов — собственные, последних двух — несобственные [7] .
В трёхмерном пространстве [ править | править код ]
Любое движение трёхмерного пространства относится к одному из следующих типов [2] :
- Параллельный перенос;
- Поворот;
- Винтовое движение — суперпозиция поворота относительно некоторой прямой и переноса на вектор, параллельный этой прямой;
- Зеркальная симметрия (отражение) относительно плоскости;
- Скользящая симметрия — суперпозиция переноса на вектор, параллельный плоскости, и симметрии относительно этой плоскости;
- Зеркальный поворот — суперпозиция поворота вокруг некоторой прямой и отражения относительно плоскости, перпендикулярной оси поворота.
Движения первых трёх типов исчерпывают класс собственных движений трёхмерного пространства (теореме Шаля), а движения последних трёх типов являются несобственными [7] .
Класс: 9
Презентация к уроку
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
- ввести понятие движения;
- развивать умения выполнять построения симметрии относительно точки, симметрии относительно прямой, построения параллельного переноса, поворот по и против часовой стрелки;
Задачи урока:
- научить строить виды движений: осевую симметрию, центральную симметрию, параллельный перенос, поворот.
Оборудование:
- оформлена доска с названием темы и целью урока;
- документ-камера, экран, ПК;
- презентация “Движение и виды движения.ppt”;
- раздаточный материал (геометрические фигуры, разного цвета, карточки с заданиями для выполнения самостоятельной работы).
Ход урока
1. Организационный момент.
Сообщение учителя о цели урока и порядке его проведения.
2. Вступительное слово учителя.
Теме “Движения” посвящена последняя 13 глава учебника по геометрии (автор Л.С. Атанасян. Геометрия. 7-9 кл.)
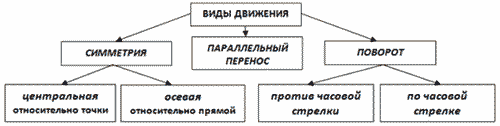
В это время на экране демонстрируется схема видов движения (Рисунок1). Учитель предлагает учащимся нарисовать эту схему в тетрадях.
Сделаем краткий исторический экскурс в теорию движений. Первым, кто начал доказывать некоторые геометрические предложения, считается древнегреческий математик Фалес Милетский (625-547 г. до н.э.).: ресурс доступа: https://ru.wikipedia.org/. Именно благодаря Фалесу геометрия начала превращаться из свода практических правил в подлинную науку. До Фалеса доказательств просто не существовало. Каким же образом проводил Фалес свои доказательства? Для этой цели он использовал движения. Движение – это преобразования фигур, при котором сохраняются расстояния между точками. Если две фигуры точно совместить друг с другом посредством движения, то эти фигуры одинаковы, равны. Именно таким путём Фалес доказал ряд первых теорем геометрии. Считается, что он первым сформулировал и доказал несколько геометрических теорем, а именно:
- вертикальные углы равны;
- имеет место равенство треугольников по одной стороне и двум прилегающим к ней углам;
- углы при основании равнобедренного треугольника равны;
- диаметр делит круг на две равные части;
- вписанный угол, опирающийся на диаметр, является прямым.
Фалес научился определять расстояние от берега до корабля, для чего использовал подобие треугольников. В основе этого способа лежит теорема, названная впоследствии теоремой Фалеса: если параллельные прямые, пересекающие стороны угла, отсекают равные отрезки на одной его стороне, то они отсекают равные отрезки и на другой его стороне.
Легенда рассказывает о том, что Фалес, будучи в Египте, поразил фараона Амасиса тем, что сумел точно установить высоту пирамиды, дождавшись момента, когда длина тени палки становится равной её высоте, и тогда измерил длину тени пирамиды.
3. Представление нового теоретического материала.
Любое отображение, при котором сохраняется расстояние между точками, называется движением. Кроме того, отображение ещё называют перемещением.
При движении отрезки переходят в отрезки, прямые — в прямые, лучи — в лучи, треугольник переходит в треугольник, сохраняется градусная мера углов, сохраняется площадь многоугольников. При изучении геометрии вы уже встречались с движением при доказательстве теорем о равенстве треугольников и фигур. Равенство фигур определяется с помощью наложений.
Учитель: фигура F равна фигуре F1 , если фигуру F можно совместить наложением с фигурой F1 . Наложение — это отображение плоскости на себя. При движении любая фигура отображается на равную ей фигуру. Параллельный перенос является движением. Поворот является движением.
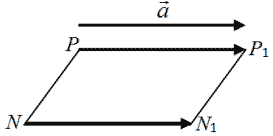
Выполним параллельный перенос (Рисунок 2).
Для того чтобы построить параллельный перенос на заданный вектор, необходимо из концов отрезка провести лучи сонаправленные заданному вектору. Измерить длину вектора и отложить на сонаправленных лучах данную длину.
Учитель: Мы познакомились с видом симметрии — параллельным переносом на заданный вектор.
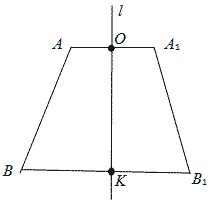
Учитель: Построим отрезок А1В1 симметричный отрезку АВ относительно прямой l. (Рисунок 3).
Для того чтобы построить отрезок А1В1 симметричный отрезку АВ относительно прямой l необходимо:
1) опустить перпендикуляр из точки А на прямую l ;
2) измерить отрезок АО с помощью циркуля;
3) отложить от точки О отрезок ОА1 = АО ;
4) опустить перпендикуляр из точки В на прямую l;
5) измерить отрезок ВК с помощью циркуля;
6) отложить от точки К отрезок КВ1 = ВК ;
Учитель: Этот вид симметрии (движения) называется — осевая симметрия относительно прямой.
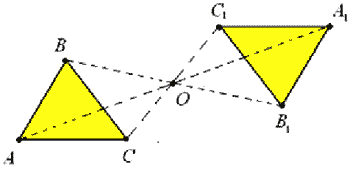
Учитель: Рассмотрим построение центральной симметрии 
Итак, мы познакомились ещё с одним видом симметрии — центральная симметрия относительно точки.
Учитель: Сравним полученные отображения. Что общего вы заметили в них?
Ученики: (Ответы учащихся).
Учитель: Правильно. Фигуры при преобразовании перешли в равные фигуры. Центральная, осевая симметрии и параллельный перенос являются движением. Это и есть тема нашего урока.
4. Итог урока: учитель подводит итог урока, опираясь на цели.
5. Домашнее задание.
п.п. 113,114 №№ 1159, 1162.
6. Задания к уроку.
Сейчас, для закрепления пройденного материала, посмотрим презентацию к уроку на тему “Движение и виды движения”, а затем каждый из вас выполнит самостоятельную работу (работа выполняется на отдельных листах).
Фамилия, Имя учащегося ______________________
Идёт приём заявок
Подать заявку
Для учеников 1-11 классов и дошкольников


Описание презентации по отдельным слайдам:
Движение. Виды движения. Движение плоскости – это отображение плоскости на себя, сохраняющее расстояния. Виды движения: 1. Симметрия: ─ осевая, ─ центральная, ─ зеркальная. ─ скользящая. 2. Параллельный перенос: 3. Поворот.
ОСЕВАЯ СИММЕТРИЯ Преобразование, при котором каждая точка А фигуры преобразуется в симметричную ей относительно некоторой оси l точку А, при этом отрезок АА ┴l , называется осевой симметрией.
Осевая симметрия в природе
Осевая симметрия в искусстве
Осевая симметрия в фигурах
ЦЕНТРАЛЬНАЯ СИММЕТРИЯ Преобразование, переводящее каждую точку А фигуры в точку А, симметричную ей относительно центра О, называется преобразованием центральной симметрии или просто центральной симметрией.
Примеры центральной симметрии
Подобие – это отображение плоскости на себя, которое не является движением.
ЗЕРКАЛЬНАЯ СИММЕТРИЯ Зеркало не просто копирует объект, а меняет местами (переставляет) передние и задние по отношению к зеркалу части объекта. Зеркальный двойник оказывается "вывернутым" вдоль направления перпендикулярного к плоскости зеркала.
Параллельный перенос Преобразование, при котором каждая точка фигуры перемещается в одном и том же направлении на одно и то же расстояние, называется параллельным переносом.
СКОЛЬЗЯЩАЯ СИММЕТРИЯ Скользящей симметрией называется такое преобразование, при котором последовательно выполняются осевая симметрия и параллельный перенос.
Определите виды движения 1 2 3 4 5 7 6 8 9 10 11
ПОВОРОТ Преобразование, при котором каждая точка Х фигуры поворачивается на один и тот же угол α вокруг заданного центра О, называется вращением или поворотом плоскости. Точка О называется центром вращения, а угол α — углом вращения.
O Поворотом плоскости вокруг точки О на угол называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М1 так, что ОМ = ОМ1 и угол МОМ1 равен . М М1
Угол поворота 600 М О М1
Поворот отрезка. O
О В А В1 А1 Угол поворота 1200
При повороте многоугольника надо повернуть каждую его вершину.
O Центр поворота фигуры может быть во внутренней области фигуры и во внешней…
- Литвиненко Оксана ДмитриевнаНаписать 30095 13.03.2016
Номер материала: ДВ-523836
- 13.03.2016 612
- 13.03.2016 2214
- 13.03.2016 895
- 13.03.2016 648
- 13.03.2016 373
- 13.03.2016 360
- 13.03.2016 444
Не нашли то что искали?
Вам будут интересны эти курсы:
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.