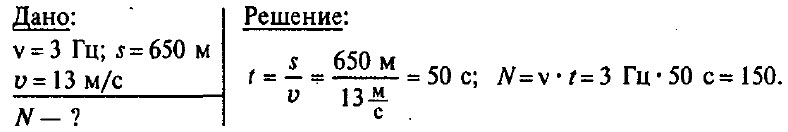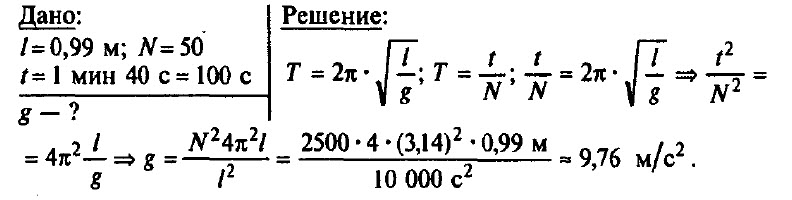Тестирование онлайн

Гармоническое колебание

Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.

График гармонического колебания

График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.

Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.

Уравнение гармонического колебания

Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .

Изменение скорости и ускорения при гармоническом колебании

Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.

Если колебание описывать по закону косинуса

Если колебание описывать по закону синуса

Максимальные значения скорости и ускорения

Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле

Как получить зависимости v(t) и a(t)

Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).

При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.

Свободные колебания происходят под действием постоянной системы сил и восстанавливающей силы.

Для получения дифференциальных уравнений колебательного движения точки воспользуемся расчётной схемой, приведённой на рис. 2.1,б.

Согласно рис. 2.1,б на точку действует постоянная система сил (G, N) и восстанавливающая сила Fyn. Дифференциальные уравнения движения точки имеют вид:

m· = Σ + Σ = – Fyn = – c·Δ = – c·Y;

m· = Σ + Σ = – G + N.


В этих уравнениях , – проекции ускорения a соответственно на координатные оси OY и OZ. Поскольку = 0, то имеем N = G = m·g. Таким образом, силы G и N образуют уравновешенную систему сил и, следовательно, эта система сил не влияет на параметры движения точки. Исходя из этого, расчётная схема для определения дифференциального уравнения движения точки упрощается (рис. 2.2).

Дифференциальное уравнение горизонтального движения точки представим в виде

+ (c/m)·Y = 0.

Введем постоянный коэффициент k 2 = или k =. Тогда имеем

+ k 2 ·Y = 0.

Это выражение называют дифференциальным уравнением свободных колебаний материальной точки.

Коэффициент k называют циклической частотой свободных колебаний, который измеряют в рад/с или в с -1 . Физический смысл коэффициента k – число полных колебаний за время t = 2π = 6,28 c.

Общее решение этого дифференциального уравнения имеет два вида.

Первый вид:

где С1, С2 – постоянные интегрирования, определяемые по начальным условиям движения.

Пусть при t0 = 0 точка имеет координату Y0 и проекцию скорости V0 на ось ОY. Тогда уравнение свободных колебаний точки получит вид

Y = ·cos(k·t) + ·sin(k·t).

Второй вид:

где А и β – постоянные интегрирования; А – амплитуда свободных колебаний; (k·t + β) – фаза колебаний; β – начальная фаза колебаний.

По заданным начальным условиям движения точки (Y0, ) постоянные интегрирования определяют по следующей совокупности формул:

A = ;

sin(β) = ; cos(β) = ; tg(β) = .

На рис. 2.3 представлен общий вид графика свободных колебаний точки.

При изучении свободных (гармонических) колебаний широко используют понятия «амплитуда А», «период Т свободных колебаний».

Амплитуда свободных колебаний – величина наибольшего отклонения точки от положения статического равновесия.

Период свободных колебаний – отрезок времени, за который точка проходит положение статического равновесия в одном и том же направлении.

Период свободных колебаний определяют по формуле

T = = .

Анализ формулы показывает, что период свободных колебаний Т является постоянной величиной. С возрастанием массы m точки период Т увеличивается и соответственно уменьшается при увеличении коэффициента «с» жесткости пружины.

Следует отметить, что свободные колебания не затухают.

Для практических расчетов рекомендуется использовать формулу

В инженерной практике довольно часто рассматривают колебательное движение тела, подвешенного на пружинах или установленного на них. Если начало системы отсчёта поместить в положение статического равновесия груза, то эти колебания также сводятся к свободным колебаниям точки, дифференциальное уравнение движения которой имеет стандартный вид + k 2 ·Y = 0 и, следовательно, стандартное решение.

Дата добавления: 2015-05-30 ; просмотров: 2583 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Задача № 1. Шарик на нити совершил 60 колебаний за 2 мин. Определите период и частоту колебаний шарика.

Задача № 2. На рисунке изображен график зависимости координаты от времени колеблющегося тела.

По графику определите: 1) амплитуду колебаний; 2) период колебаний; 3) частоту колебаний; 4) запишите уравнение координаты.

Задача № 3. Амплитуда незатухающих колебаний точки струны 2 мм, частота колебаний 1 кГц. Какой путь пройдет точка струны за 0,4 с? Какое перемещение совершит эта точка за один период колебаний?

Задача № 4. Пользуясь графиком изменения координаты колеблющегося тела от времени, определить амплитуду, период и частоту колебаний. Записать уравнение зависимости x(t) и найти координату тела через 0,1 и 0,2 с после начала отсчета времени.

Задача № 5. Какова длина математического маятника, совершающего гармонические колебания с частотой 0,5 Гц на поверхности Луны? Ускорение свободного падения на поверхности Луны 1,6 м/с 2 .

Задача № 6. Груз массой 400 г совершает колебания на пружине с жесткостью 250 Н/м. Амплитуда колебаний 15 см. Найти полную механическую энергию колебаний и наибольшую скорость движения груза.

Задача № 7. Частота колебаний крыльев вороны в полете равна в среднем 3 Гц. Сколько взмахов крыльями сделает ворона, пролетев путь 650 м со скоростью 13 м/с?

Задача № 8. Гармоническое колебание описывается уравнением
Чему равны циклическая частота колебаний, линейная частота колебаний, начальная фаза колебаний?

Задача № 9. Математический маятник длиной 0,99 м совершает 50 полных колебаний за 1 мин 40 с. Чему равно ускорение свободного падения в данном месте на поверхности Земли? (Можно принять π 2 = 9,87.)

Задача № 10. ОГЭ Как и во сколько раз изменится период колебаний пружинного маятника, если шарик на пружине заменить другим шариком, радиус которого вдвое меньше, а плотность — в два раза больше?

Задача № 11. ЕГЭ Два математических маятника за одно и то же время совершают — первый N1 = 30, а второй — N2 = 40 колебаний. Какова длина каждого из них, если разность их длин Δl = 7 см?

Краткая теория для решения Задачи на Механические колебания.

Это конспект по теме «ЗАДАЧИ на Механические колебания». Выберите дальнейшие действия: