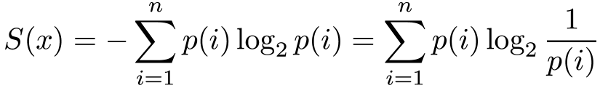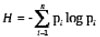Понятие Энтропи́и впервые введено в 1865 Р. Клаузиусом в термодинамике для определения меры необратимого рассеяния энергии. Энтропия применяется в разных отраслях науки, в том числе и в теории информации как мера неопределенности какого-либо опыта, испытания, который может иметь разные исходы. Эти определения энтропии имеют глубокую внутреннюю связь. Так на основе представлений об информации можно вывести все важнейшие положения статистической физики. [БЭС. Физика. М: Большая российская энциклопедия, 1998].
Эта величина также называется средней энтропией сообщения. Энтропия в формуле Шеннона является средней характеристикой – математическим ожиданием распределения случайной величины .
Например, в последовательности букв, составляющих какое-либо предложение на русском языке, разные буквы появляются с разной частотой, поэтому неопределённость появления для некоторых букв меньше, чем для других.
В 1948 году, исследуя проблему рациональной передачи информации через зашумлённый коммуникационный канал, Клод Шеннон предложил революционный вероятностный подход к пониманию коммуникаций и создал первую, истинно математическую, теорию энтропии. Его сенсационные идеи быстро послужили основой разработки теории информации, которая использует понятие вероятности. Понятие энтропии, как меры случайности, введено Шенноном в его статье «A Mathematical Theory of Communication», опубликованной в двух частях в Bell System Technical Journal в 1948 году.
В случае равновероятных событий (частный случай), когда все варианты равновероятны, остается зависимость только от количества рассматриваемых вариантов и формула Шеннона значительно упрощается и совпадает с формулой Хартли, которая впервые была предложена американским инженером Ральфом Хартли в 1928 году, как один из научных подходов к оценке сообщений:
, где I – количество передаваемой информации, p – вероятность события, N – возможное количество различных (равновероятных) сообщений.
Задание 1. На равновероятные события.
В колоде 36 карт. Какое количество информации содержится в сообщении, что из колоды взята карта с портретом “туз”; “туз пик”?
Вероятность p1 = 4/36 = 1/9, а p2 = 1/36. Используя формулу Хартли имеем:
Ответ: 3.17; 5.17 бит
Заметим (из второго результата), что для кодирования всех карт, необходимо 6 бит.
Из результатов также ясно, что чем меньше вероятность события, тем больше информации оно содержит. (Данное свойство называется монотонностью)
Задание 2. На неравновероятные события
В колоде 36 карт. Из них 12 карт с “портретами”. Поочередно из колоды достается и показывается одна из карт для определения изображен ли на ней портрет. Карта возвращается в колоду. Определить количество информации, передаваемой каждый раз, при показе одной карты.
Ответ: I = 0.91 бита.
Свойство аддитивности информации.
Для независимых справедливо:
Задание 3. На аддитивность.
Документация некоторого учреждения размещена в 4-х комнатах. В каждой комнате находится 16 шкафов. Каждый шкаф имеет 8 полок. Определить количество информации, которое несет сообщение о том, что нужный документ находится в третьей комнате, в тринадцатом шкафу на пятой полке.
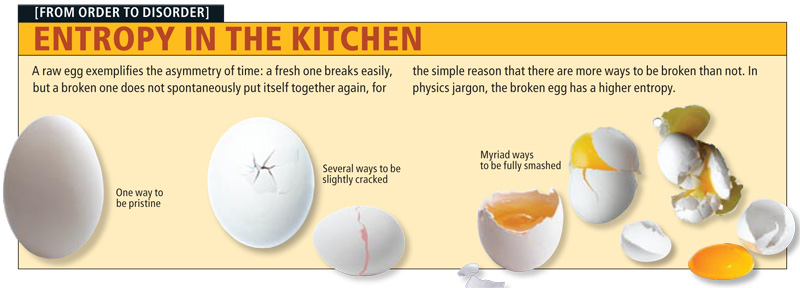
Как может показаться, анализ сигналов и данных — тема достаточно хорошо изученная и уже сотни раз проговоренная. Но есть в ней и некоторые провалы. В последние годы словом «энтропия» бросаются все кому не лень, толком и не понимая, о чем говорят. Хаос — да, беспорядок — да, в термодинамике используется — вроде тоже да, применительно к сигналам — и тут да. Хочется хотя бы немного прояснить этот момент и дать направление тем, кто захочет узнать чуть больше об энтропии. Поговорим об энтропийном анализе данных.
В русскоязычных источниках очень мало литературы на этот счет. А цельное представление вообще получить практически нереально. Благо, моим научным руководителем оказался как раз знаток энтропийного анализа и автор свеженькой монографии [1], где все расписано «от и до». Счастью предела не было, и я решила попробовать донести мысли на этот счет до более широкой аудитории, так что пару выдержек возьму из монографии и дополню своими исследованиями. Может, кому и пригодится.
Итак, начнем с начала. Шенноном в 1963 г. было предложено понятие меры усредненной информативности испытания (непредсказуемости его исходов), которая учитывает вероятность отдельных исходов (до него был еще Хартли, но это опустим). Если энтропию измерять в битах, и взять основание 2, то получим формулу для энтропии Шеннона 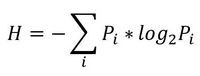
То есть в этом случае энтропия напрямую связана с «неожиданностью» возникновения события. А отсюда вытекает и его информативность — чем событие более предсказуемо, тем оно менее информативно. Значит и его энтропия будет ниже. Хотя открытым остается вопрос о соотношениях между свойствами информации, свойствами энтропии и свойствами различных ее оценок. Как раз с оценками мы и имеем дело в большинстве случаев. Все, что поддается исследованию — это информативность различных индексов энтропии относительно контролируемых изменений свойств процессов, т.е. по существу, их полезность для решения конкретных прикладных задач.
Энтропия сигнала, описываемого некоторым образом (т.е. детерминированного) стремится к нулю. Для случайных процессов энтропия возрастает тем больше, чем выше уровень «непредсказуемости». Возможно, именно из такой связки трактовок энтропии вероятность->непредсказуемость->информативность и вытекает понятие «хаотичности», хотя оно достаточно неконкретно и расплывчато (что не мешает его популярности). Встречается еще отождествление энтропии и сложности процесса. Но это снова не одно и то же.
Энтропия бывает разная черная белая красная:
- термодинамическая
- алгоритмическая
- информационная
- дифференциальная
- топологическая
Все они различаются с одной стороны, и имеют общую основу с другой. Конечно, каждый вид применяется для решения определенных задач. И, к сожалению, даже в серьезных работах встречаются ошибки в интерпретации результатов расчета. А все связано с тем, что на практике в 90% случаев мы имеем дело с дискретным представлением сигнала непрерывной природы, что существенно влияет на оценку энтропии (на деле там в формулке появляется поправочный коэффициент, который обычно игнорируют).
Для того, чтобы немного обрисовать области применения энтропии к анализу данных, рассмотрим небольшую прикладную задачку из монографии [1] (которой нет в цифровом виде, и скорей всего не будет).
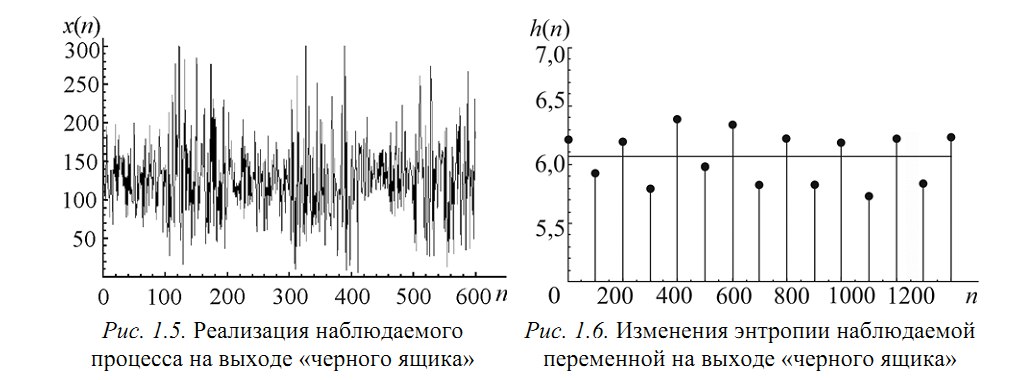
Пусть есть система, которая каждые 100 тактов переключается между несколькими состояниями и порождает сигнал x (рисунок 1.5), характеристики которого изменяются при переходе. Но какие — нам не известно.
Разбив x на реализации по 100 отсчетов можно построить эмпирическую плотность распределения и по ней вычислить значение энтропии Шеннона. Получим значения, «разнесенные» по уровням (рисунок 1.6).
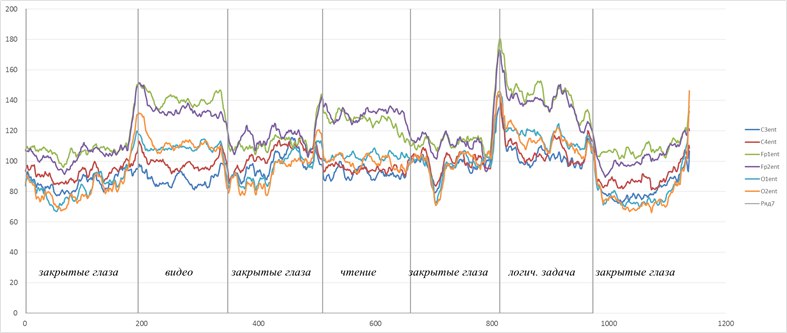
Как можно видеть, переходы между состояниями явно наблюдаются. Но что делать в случае, если время переходов нам не известно? Как оказалось, вычисление скользящим окном может помочь и энтропия так же «разносится» на уровни.В реальном исследовании мы использовали такой эффект для анализа ЭЭГ сигнала (разноцветные картинки про него будут дальше).
Теперь еще про одно занятное свойство энтропии — она позволяет оценить степень связности нескольких процессов. При наличии у них одинаковых источников мы говорим, что процессы связаны (например, если землетрясение фиксируют в разных точках Земли, то основная составляющая сигнала на датчиках общая). В таких случаях обычно применяют корреляционный анализ, однако он хорошо работает только для выявления линейных связей. В случае же нелинейных (порожденных временными задержками, например) предлагаем пользоваться энтропией.
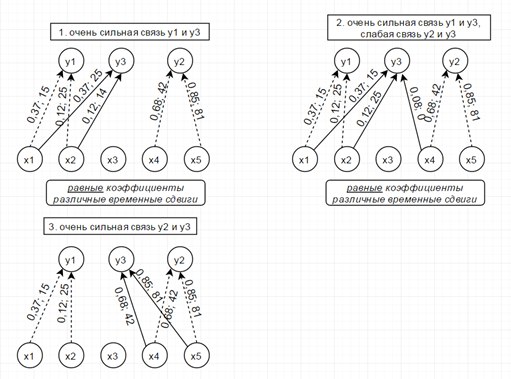
Рассмотрим модель из 5ти скрытых переменных(их энтропия показана на рисунке ниже слева) и 3х наблюдаемых, которые генерируются как линейная сумма скрытых, взятых с временными сдвигами по схеме, показанной ниже справа. Числа-это коэффициенты и временные сдвиги (в отсчетах).
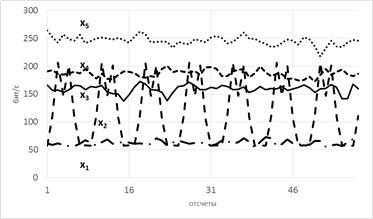
Так вот, фишка в том, что энтропия связных процессов сближается при усилении их связи. Черт побери, как это красиво-то!
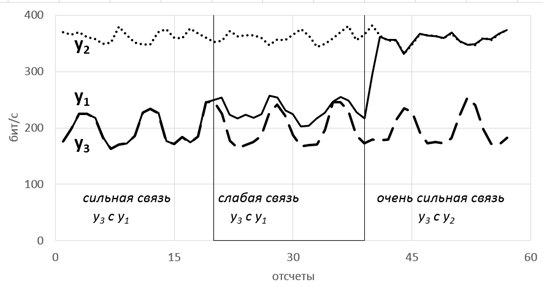
Такие радости позволяют вытащить практически из любых самых странных и хаотичных сигналов (особенно полезно в экономике и аналитике) дополнительные сведения. Мы их вытаскивали из электроэнцефалограммы, считая модную нынче Sample Entropy и вот какие картинки получили.
Можно видеть, что скачки энтропии соответствуют смене этапов эксперимента. На эту тему есть пара статей и уже защищена магистерская, так что если кому будут интересны подробности — с радостью поделюсь. А так по миру по энтропии ЭЭГ ищут уже давно разные вещи — стадии наркоза, сна, болезни Альцгеймера и Паркинсона, эффективность лечения от эпилепсии считают и тд. Но повторюсь-зачастую расчеты ведутся без учета поправочных коэффициентов и это грустно, так как воспроизводимость исследований под большим вопросом (что критично для науки, так то).
Резюмируя, остановлюсь на универсальности энтропийного аппарата и его действительной эффективности, если подходить ко всему с учетом подводных камней. Надеюсь, что после прочтения у вас зародится зерно уважения к великой и могучей силе Энтропии.
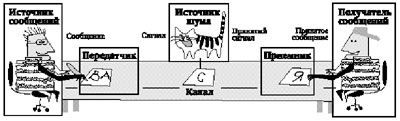
Дискретное сообщение — это любой набор символов, который формируется Источником (им может быть, например, человек). От Источника сообщение переходит к Передатчику, который преобразует его к виду, который уже можно передавать по Каналу связи. Например, Передатчик может кодировать сообщение. Преобразованное сообщение называется Сигналом. Канал связи — это технический комплекс аппаратуры, который позволяет передать Сигнал. В общем случае в процессе передачи сигнал в канале искажается шумом, который исходит от Источника шума. Приемник обычно выполняет операцию, обратную по отношению к той, что производится передатчиком, — т. е. восстанавливает сообщение по сигналам. Процесс преобразования сигнала в сообщения, осуществляемый в Приемнике, называют декодированием. Получатель — это человек или аппарат, для которого предназначено сообщение.
Энтропия
В 1946 г. американский ученый-статистик Джон Тьюки предложил название БИТ (BIT — аббревиатура от BInary digiT), одно из главных понятий XX века. Тьюки избрал бит для обозначения одного двоичного разряда, способного принимать значение 0 или 1. Шеннон использовал бит как единицу измерения информации. Мерой количества информации Шеннон предложил считать функцию, названную им энтропией.
Пусть сообщение — осмысленное предложение на русском языке. Шеннон заметил, что при передаче различных букв мы передаем разное количество информации. Если мы передаем часто встречающиеся буквы, то информация меньше; при передаче редких букв — больше. Это видно при кодировании букв алфавита азбукой Морзе. Наиболее частые буквы передаются коротко, а для редких используют более длинные цепочки. Так, буква «Е» кодируется одной точкой «.», а редкая «Ш» — четырьмя тире «––––» (это самая длинная последовательность на букву в азбуке Морзе).
Количество информации на букву связано с частотой употреблений этой буквы во всех сообщениях, формируемых на языке. Чем более редкую букву мы передаем, тем больше в ней информации.
Энтропия — мера непредсказуемости. Это понятие Шеннон взял из статистической термодинамики. Пусть вероятность i-того символа алфавита, состоящего из n символов (мера частоты, с которой встречается символ во всех сообщениях языка), равна pi. Тогда информация одного символа:
(здесь log — логарифм по основанию 2).
Шеннон пишет: «Величина H играет центральную роль в теории информации в качестве меры количества информации, возможности выбора и неопределенности». Количество информации, передаваемое в сообщении, тесно связано с мерой неопределенности, или непредсказуемости передаваемых символов.
Избыточность
Пусть источник сообщения передает предложение реального языка. Оказывается, каждый следующий символ не полностью случаен, и вероятность его появления не полностью предопределена средней частотой символа во всех сообщениях языка. То, какой символ последует дальше, зависит от символов, уже переданных. Например, в русском языке после символа «Ъ» не может идти символ согласного звука. После двух подряд гласных «Е» третий гласный «Е» следует крайне редко (например, в слове «длинношеее»). Таким образом, каждый следующий символ в некоторой степени предопределен, поэтому можно говорить об условной энтропии символа.
Источник может порождать сообщения строго определенного типа — например, формальную деловую переписку; в таком случае предопределенность следующего символа может быть намного выше, чем в среднем в языке. Тогда энтропия этого источника будет отличаться от максимальной: она будет меньше. Если мы сравним энтропию конкретного источника и максимальную энтропию, то определим избыточность сообщения.

Сенсация — это редкое событие, предсказуемость которого очень мала, и потому велика его информационная стоимость. Часто информацией называют новости — сообщения о только что произошедших событиях, о которых мы еще не знаем. Но если о случившемся нам расскажут во второй и третий раз, избыточность сообщения станет очень велика, его непредсказуемость упадет до нуля, и мы просто не станем слушать, отмахиваясь от говорящего со словами: «Знаю, знаю». Поэтому-то средства массовой информации (СМИ) и стараются быть первыми. Вот это соответствие интуитивному чувству новизны, которое рождается неожиданным известием, и сыграло главную роль в том, что статья Шеннона, не рассчитанная на массового читателя, стала сенсацией, которую подхватила пресса и которую приняли как универсальный ключ к познанию природы ученые самых разных специальностей — от лингвистов и литературоведов до биологов.
Но понятие информации, по Шеннону, — это строгая математическая теория, и ее применение за пределами теории связи очень рискованно. Зато в самой теории связи она играет центральную роль.