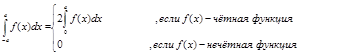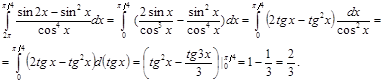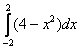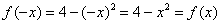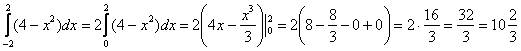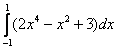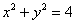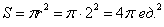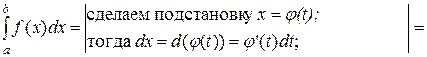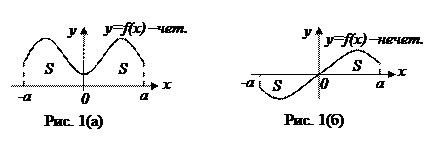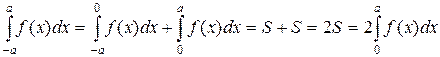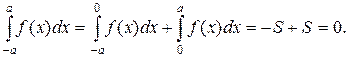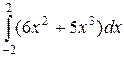При вычислении определенных интегралов от четных и нечетных функций полезно иметь в виду следующие формулы:
(в предположении, что f(x) – непрерывная на симметричном относительно начала координат отрезке [-a;a] функция).
Пример 5. Вычислить: 
Решение: подынтегральная функция чётная, поэтому
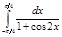

1.6. Интеграл от периодической функции по периоду
Пусть фуккция f(x) – непрерывная, периодическая с периодом Т, т.е. f(x+T)=f(x).
Для такой функции имеет место следующее свойство: интеграл от периодической функции по периоду не зависит от положения интервала интегрирования: 

Решение: подынтегральная функция имеет период T=π, поэтому из верхнего и нижнего периодов можно вычесть 2π, полученный интеграл будет равен данному:
ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
2.1. Геометрические приложения определенного интеграла
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 9826 — 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Сначала вспомним, что такое чётность функции. Функция является чётной, если для неё выполнено условие 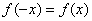
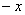
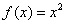
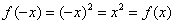
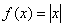
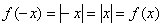
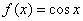
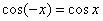
таким образом, все перечисленные функции являются чётными.
Теперь рассмотрим определённый интеграл вида 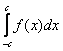
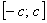
Если подынтегральная функция 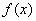
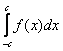
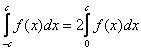
Почему? …догадались? Рассмотрим конкретный пример с чертежом:
Пример 21
Вычислить определенный интеграл
Хоть и очевидно, но проверим функцию 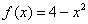
И, согласно правилу, на симметричном относительно нуля отрезке 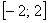
А сейчас геометрическая интерпретация: график любой чётной функция, в частности 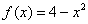
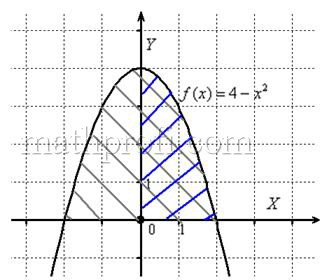
Определенный интеграл 
Возможно, некоторые скажут: «Да зачем это всё нужно? – можно ведь и так вычислить определенный интеграл». Можно. Давайте вычислим: 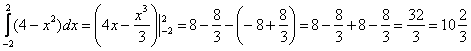
Но удобно ли было подставлять отрицательный нижний предел? Не очень-то. И «минус» тут частенько теряют. Поэтому гораздо проще и приятнее подставить ноль.
Замечу также, что это ещё был простой демонстрационный пример, на практике всё бывает хуже, особенно, когда имеешь дело с двойными и тройными интегралами, где вычислений и так хватает.
Разминочный интеграл для самостоятельного решения:
Пример 22
И обратите внимание, что когда вам предложено ПРОСТО ВЫЧИСЛИТЬ определенный интеграл, то чертеж выполнять не нужно! Достаточно убедиться в чётности функции (как правило, устно) и перед решением сделать соответствующий письменный комментарий. Кстати, о птичках:
Пример 23
1) Вычислить определенный интеграл: 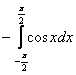
2) Вычислить площадь плоской фигуры, ограниченной линией 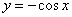
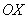
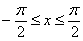
Внимание! Это две РАЗНЫЕ задачи! Решаем:
1) Подынтегральная функция является чётной, отрезок интегрирования симметричен относительно нуля, поэтому:
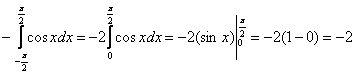
2) Теперь задача на нахождение площади фигуры: 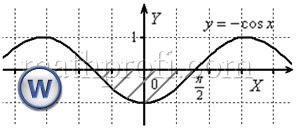
На отрезке 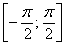
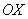
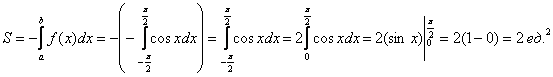
Заметьте, что чётность косинуса никто не отменял, поэтому мы опять споловинили отрезок и удвоили интеграл.
Творческий пример для самостоятельного решения + новинка:
Пример 24
Вычислить площадь круга, ограниченного окружностью
Напоминаю, что уравнение 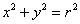
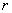
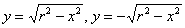
Новизна же состоит в ранее не встречавшейся замене 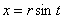
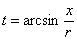
Забавно, что формула и выводится с помощью этого интеграла.
Полную и свежую версию данного курса в pdf-формате ,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Читайте также:
- Float average_value(int, int); // Прототип функции
- I. Взгляды командования иностранных армий на использование мотопехотной (танковой) ротной тактической группы в обороне. Возможный состав ротных тактических групп.
- I. Место и роль МПВО в советском военном строительстве. Структура и функции МПВО к началу Великой Отечественной войны.
- II. ФУНКЦИИ ЦЕНТРАЛЬНОГО БАНКА.
- Ordm;. Сведение кратных интегралов к повторным интегралам.
- Абсолютная сходимость несобственных интегралов.
- Алгоритм разложения функции в ряд Тейлора
- Алгоритмы распределения памяти с использованием внешней памяти
- Аналитическое получение дискретной передаточной функции из непрерывной с помощью ZOH
- Асимптоты графика функции
- Асимптоты графика функции.
- Атмосфера, ее состав и строение. Функции атмосферы.
Лекция 40. Вычисление определенного интеграла. Замена переменной в определенном интеграле. Интегрирование по частям. Некоторые приложения определенных интегралов. Понятие о несобственных интегралах.
Подстановка в определенных интегралах.
Пусть y = f(x) – непрерывная на промежутке [a; b] оси ox функция, а 

| x | a b |
| t | α β |

Докажем правомочность схемы (1). Пусть
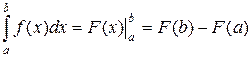 | (2) |
Здесь F(x) – некоторая первообразная для функции f(x). То есть F΄(x) = f(x). Но тогда, по правилу вычисления производной сложной функции,
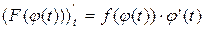 | (3) |
Поэтому по формуле Ньютона-Лейбница
 | (4) |
Равенство результатов (2) и (4) и доказывает правомочность схемы (1).
Кстати, сравнивая схему (1) вычисления определенных интегралов с помощью подстановки с аналогичной схемой вычисления неопределенных интегралов, можно увидеть и то, что в этих схемах общее, и то, что различно.
Примечание. На практике часто бывает удобнее делать подстановку не вида x = φ(t), а вида t = φ(x).
Вычисление определенных интегралов по частям.
Мы уже знаем, что по частям можно вычислять неопределенные интегралы. Для этого используется уже полученная формула 
 | (5) |
Здесь 

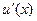



Докажем формулу (5). Учтем, что
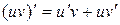 | (6) |
Функция 


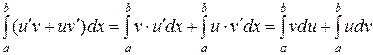 | (7) |
С другой стороны, согласно (6), функция 

 | (8) |
Сравнивая (7) и (8), приходим к доказываемой формуле (5).
Пример 1. Вычислить 
а) Если f(x) – непрерывная и четная на промежутке [-a; а] функция, то
 | (9) |
б) Если f(x) – непрерывная и нечетная на промежутке [-a; a] функция, то
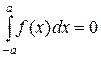 | (10) |
Доказательство. Рассмотрим рисунки 1(а) и 1(б), соответствующие случаям (а) и (б) соответственно.
а) Если f(x) – четная на [-a; a] функция, то согласно рис.1(а) и формулы (3) получаем:
б) Если f(x) – нечетная на [a; b] функция, то согласно рис. 1(б) и формулам (3) и (5) получаем:
Пример 2. Упростить, а затем и вычислить
Дата добавления: 2013-12-13 ; Просмотров: 757 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет