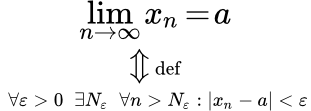Используя определение предела последовательности докажите что

Здесь мы рассмотрим определение конечного предела последовательности. Случай последовательности, сходящейся к бесконечности, рассмотрен на странице «Определение бесконечно большой последовательности».

Определение предела последовательности

ε — окрестность точки a – это открытый интервал ( a – ε, a + ε ). Сходящаяся последовательность – это последовательность, у которой существует предел . Также говорят, что последовательность сходится к a . Расходящаяся последовательность – это последовательность, не имеющая предела.

Из определения следует, что, если последовательность имеет предел a , то какую бы ε — окрестностью точки a мы не выбрали, за ее пределами может оказаться, лишь конечное число элементов последовательности, или вообще ни одного (пустое множество). А любая ε — окрестность содержит бесконечное число элементов. В самом деле, задав определенное число ε , мы, тем самым имеем число . Так что все элементы последовательности с номерами , по определению, находятся в ε — окрестностью точки a . Первые элементов могут находиться где угодно. То есть за пределами ε — окрестности может находиться не более элементов – то есть конечное число.

Также заметим, что разность вовсе не обязана монотонно стремиться к нулю, то есть все время убывать. Она может стремиться к нулю не монотонно: может то возрастать, то убывать, имея локальные максимумы. Однако эти максимумы, с ростом n , должны стремиться к нулю (возможно тоже не монотонно).

С помощью логических символов существования и всеобщности, определение предела можно записать следующим образом:
(1) .

Определение, что число a не является пределом

Теперь рассмотрим обратное утверждение, что число a не является пределом последовательности.

Число a не является пределом последовательности , если существует такое , что для любого натурального n существует такое натуральное m > n , что
.

Запишем это утверждение с помощью логических символов.
(2) .

Утверждение, что число a не является пределом последовательности, означает, что
можно выбрать такую ε — окрестность точки a , за пределами которой будет находиться бесконечное число элементов последовательности.

Рассмотрим пример. Пусть задана последовательность с общим элементом
(3)
Любая окрестность точки содержит бесконечное число элементов. Однако эта точка не является пределом последовательности, поскольку и любая окрестность точки также содержит бесконечное число элементов. Возьмем ε — окрестность точки с ε = 1 . Это будет интервал ( –1, +1) . Все элементы, кроме первого, с четными n принадлежат этому интервалу. Но все элементы с нечетными n находятся за пределами этого интервала, поскольку они удовлетворяют неравенству x_n > 2 . Поскольку число нечетных элементов бесконечно, то за пределами выбранной окрестности будет находиться бесконечное число элементов. Поэтому точка не является пределом последовательности.

Теперь покажем это, строго придерживаясь утверждения (2). Точка не является пределом последовательности (3), поскольку существует такое , так что, для любого натурального n , существует нечетное , для которого выполняется неравенство
.

Также можно показать, что любая точка a не может являться пределом этой последовательности. Мы всегда можем выбрать такую ε — окрестность точки a , которая не содержит либо точку 0, либо точку 2. И тогда за пределами выбранной окрестности будет находиться бесконечное число элементов последовательности.

Эквивалентное определение предела последовательности

Можно дать эквивалентное определение предела последовательности, если расширить понятие ε — окрестности. Мы получим равносильное определение, если в нем, вместо ε — окрестности, будет фигурировать любая окрестность точки a . Окрестности точки – это любой открытый интервал, содержащий эту точку. Математически окрестность точки определяется так: , где ε ₁ и ε ₂ – произвольные положительные числа.

Тогда эквивалентное определение предела будет следующим.

Предел последовательности – это такое число a , если для любой его окрестности существует такое натуральное число N , так что все элементы последовательности с номерами принадлежат этой окрестности.

Это определение можно представить и в развернутом виде.

Предел последовательности – это такое число a , если для любых положительных чисел и существует такое натуральное число N , зависящее от и , что для всех натуральных выполняются неравенства
.

Доказательство равносильности определений

Докажем, что, представленные выше, два определения предела последовательности равносильны.

Пусть число a является пределом последовательности согласно первому определению. Это означает, что имеется функция , так что для любого положительного числа ε выполняются неравенства:
(4) при .

Покажем, что число a является пределом последовательности и по второму определению. То есть нам нужно показать, что существует такая функция , так что для любых положительных чисел ε ₁ и ε ₂ выполняются неравенства:
(5) при .

Пусть мы имеем два положительных числа: ε ₁ и ε ₂ . И пусть ε – наименьшее из них: . Тогда ; ; . Используем это в (5):
.
Но неравенства выполняются при . Тогда и неравенства (5) выполняются при .

То есть мы нашли такую функцию , при которой выполняются неравенства (5) для любых положительных чисел ε ₁ и ε ₂ .
Первая часть доказана.

Теперь пусть число a является пределом последовательности согласно второму определению. Это означает, что имеется функция , так что для любых положительных чисел ε ₁ и ε ₂ выполняются неравенства:
(5) при .

Покажем, что число a является пределом последовательности и по первому определению. Для этого нужно положить . Тогда при выполняются неравенства:
.
Это соответствует первому определению с .
Равносильность определений доказана.

Примеры

Все примеры Здесь мы рассмотрим несколько примеров, в которых требуется доказать, что заданное число a является пределом последовательности. При этом нужно задать произвольные положительное число ε и определить функцию N от ε такую, что для всех выполняется неравенство .

Пример 1

Выпишем определение предела последовательности:
(1) .
В нашем случае ;
.

Вводим положительные числа и :
.
Воспользуемся свойствами неравенств. Тогда если и , то
.

То есть, для любого положительного , мы можем взять любое натуральное число, большее или равное :
.
Тогда
при .
Это означает, что число является пределом заданной последовательности:
.

Пример 2

Все примеры ⇑ С помощью определения предела последовательности доказать, что
.

Выпишем определение предела последовательности:
(1) .
В нашем случае , ;
.

Вводим положительные числа и :
.
Воспользуемся свойствами неравенств. Тогда если и , то
.

То есть, для любого положительного , мы можем взять любое натуральное число, большее или равное :
.
Тогда
при .
Это означает, что число является пределом последовательности :
.

Пример 3

Все примеры ⇑ Используя определение предела последовательности доказать, что
.

Вводим обозначения , .
Преобразуем разность:
.
Для натуральных n = 1, 2, 3, . имеем:
.

Выпишем определение предела последовательности:
(1) .
Вводим положительные числа и :
.
Тогда если и , то
.

То есть, для любого положительного , мы можем взять любое натуральное число, большее или равное :
.
При этом
при .
Это означает, что число является пределом последовательности :
.

Пример 4

Все примеры ⇑ Используя определение предела последовательности доказать, что
.

Выпишем определение предела последовательности:
(1) .
В нашем случае , ;
.

Вводим положительные числа и :
.
Тогда если и , то
.

Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Автор: Олег Одинцов . Опубликовано: 12-07-2017 Изменено: 08-12-2017

Доброго времени суток!

Доказать через определение предела, подробнее, пожалуйста, т.к. не понимаю, что делать нужно.

lim x стремится к бесконечности (x^2+x+1)/(2x+5) = бесконечности
Lim x стремится к единице (x^4+2x^3+5) = 8
Lim x стремится к бесконечности (2x-1)/(x+3) = 2

Заранее спасибо ! 🙂

задан 19 Ноя ’13 12:40

1) разделите числитель и знаменатель на $%x$%. Числитель будет стремиться к бесконечности, знаменатель — к двум, т.е. частное тоже к бесконечности.

2) просто подставьте $%x=1$%.

3) числитель и знаменатель делим на $%x$% и применяем теорему о пределе частного: предел числителя равен 2, предел знаменателя равен 1.

Нужно доказать, а не решить, вот в чем проблема, с помощью, как я поняла определения Коши.

Слово "доказать" означает вывести из известных положений: аксиом, опредлений, лемм, теорем. Все перечисленные утверждения выводятся из теорем о пределах. Если же этими теоремами пользоваться не разрешено, то в условии задачи такая вещь должна быть явно оговорена. Рассуждения при этом становятся несколько более сложными, но возможно доказательство, опирающееся только на определение предела и на элементарные свойства неравенств. Если нужно, я по каждому пункту могу продемонстрировать, как это делается.

1 ответ

3) Докажем из определения, что $$limlimits_frac<2x-1>=2.$$ Рассмотрим разность $$2-frac<2x-1>=frac<7><2(x+3)>.$$ Мы хотим, чтобы эта величина стала по модулю меньше произвольно заданного положительного $%varepsilon$%, поэтому напишем желаемое неравенство и поймём, при каких $%x$% (достаточно больших по модулю) оно заведомо будет выполнено. Легко понять, что неравенство $$frac7 <2|x+3|>frac7<2varepsilon>$%. Это значит, что $%x+3 > frac7<2varepsilon>$% или $%x+3 3+frac7<2varepsilon>$%, то из свойств неравенств будет ясно, что для положительных $%x$% будет верно первое из условий (даже с "запасом"), а для отрицательных — второе условие. Тогда из определения предела следует доказываемый факт.

отвечен 19 Ноя ’13 15:46

falcao
242k ● 1 ● 34 ● 48

Если вас не затруднит, то напишите, пожалуйста, как это же доказательство нужно сделать, но для лимита равного не конкретному числу, как в этом примере числу 2, а бесконечности. А будет ещё лучше, если для оставшихся двух моих примеров, чтоб уж наверняка понимать как и что делать. Заранее спасибо 🙂

Это достаточно просто: пусть в примере 1 число $%x$% достаточно большое — например, $%xge5$%. Тогда знаменатель не превосходит $%3x$%, а числитель больше $%x^2$%. Сама дробь при этом больше $%x/3$%. Чтобы она оказалась больше заданного числа $%M$%, достаточно положить $%xge3M$%. Скажем, при $%xge3000$% значение дроби будет больше тысячи и т.п.

Пример 2 там тоже простой. Рассмотрим разность функции и значения предполагаемого предела. Получится $%(x^4-1)+2(x^3-1)$%. Выделим множитель $%x-1$% и посмотрим на то, что осталось. Там будет $%x^3+x^2+x+1+2(x^2+x+1)=x^3+3x^2+3x+3$%, хотя конкретный вид не так важен. Потребуем сначала, чтобы было $%|x-1| (20 Ноя ’13 17:30) falcao

Reshak.ru — сборник решебников для учеников старших классов. Здесь можно найти решебники, ГДЗ, переводы текстов по школьной программе. Практически весь материал, собранный на сайте — сделанный для людей. Все решебники выполнены качественно, с приятной навигацией. Вы сможете скачать гдз, решебник английского, улучшить ваши школьные оценки, повысить знания, получить намного больше свободного времени.

Главная задача сайта: помогать школьникам в решении домашнего задания. Кроме того, весь материал гдз совершенствуется, добавляются новые сборники решений.