Направление выпуклости графика функции. Точки перегиба
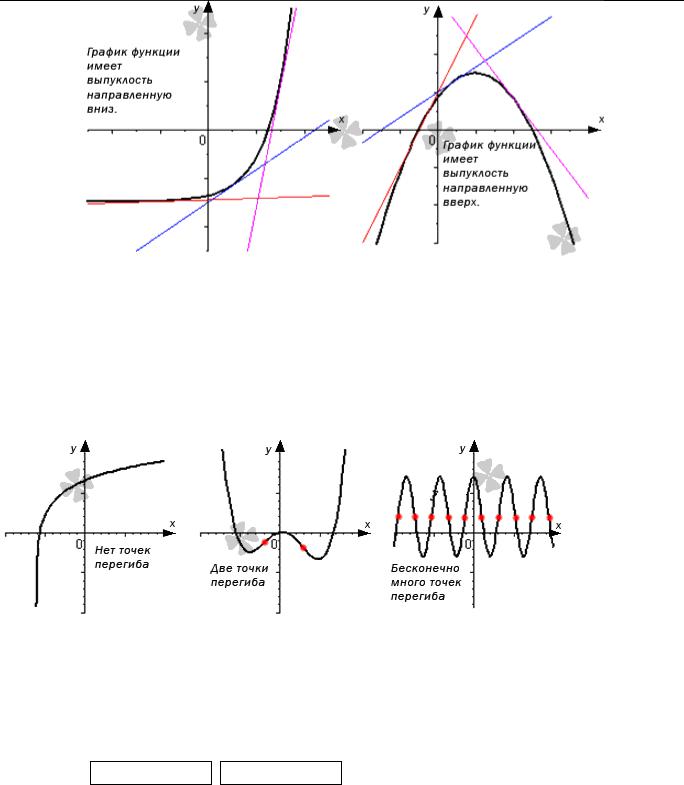
Определение : Кривая y=f(x) называется выпуклой вверх в промежутке (a; b), если она лежит ниже касательной в любой точке этого промежутка. 
Определение : Промежутки, в которых график функции обращен выпуклостью вверх или вниз, называются промежутками выпуклости графика функции.
Выпуклость вниз или вверх кривой, являющейся графиком функции y=f(x) , характеризуется знаком ее второй производной: если в некотором промежутке f’’(x) > 0, то кривая выпукла вниз на этом промежутке; если же f’’(x) Определение: Точка графика функции y=f(x) , разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба.
Точками перегиба могут служить только критические точки II рода, т.е. точки, принадлежащие области определения функции y = f(x) , в которых вторая производная f’’(x) обращается в нуль или терпит разрыв.
Правило нахождения точек перегиба графика функции y = f(x)
- Найти вторую производную f’’(x) .
- Найти критические точки II рода функции y=f(x) , т.е. точки, в которой f’’(x) обращается в нуль или терпит разрыв.
- Исследовать знак второй производной f’’(x) в промежутка, на которые найденные критические точки делят область определения функции f(x) . Если при этом критическая точка x0 разделяет промежутки выпуклости противоположных направлений, то x0 является абсциссой точки перегиба графика функции.
- Вычислить значения функции в точках перегиба.
Пример 1 . Найти промежутки выпуклости и точки перегиба следующей кривой: f(x) = 6x 2 –x 3 .
Решение: Находим f ‘(x) = 12x – 3x 2 , f ‘’(x) = 12 – 6x.
Найдем критические точки по второй производной, решив уравнение 12-6x=0 . x=2 .
f(2) = 6*2 2 – 2 3 = 16
Ответ: Функция выпукла вверх при x∈(2; +∞) ; функция выпукла вниз при x∈(-∞; 2) ; точка перегиба (2;16) .
Пример 2 . Имеет ли точки перегиба функция: f(x)=x 3 -6x 2 +2x-1
Пример 3 . Найти промежутки, на которых график функции является выпуклым и выгнутым: f(x)=x 3 -6x 2 +12x+4
Тема: «Исследование функции»
Исследование функции на экстремумы
Определение 1 . Функция y f x возрастает на интервале X , если для любых x 1 X и x 2 X
( x 2 x 1 ) выполняется неравенство
! Большему значению аргумента соответствует большее значение функции.
Определение 2 . Функция y f x убывает на интервале X , если для любых x 1 X
( x 2 x 1 ) выполняется неравенство
! Большему значению аргумента соответствует меньшее значение функции.
ЗАМЕЧАНИЕ: если функция определена и непрерывна в концах интервала возрастания или убывания a ; b , т. е. при x a и x b , то эти точки включаются в промежуток возрастания или убывания. Это не противоречит определениям возрастающей и убывающей функции на промежутке X .
Определение 3 . Точку x 0 называют точкой максимума функции y f x , если для всех x из ее окрестности справедливо неравенство f x 0 f x . Значение функции в точке максимума называют максимумом функции и обозначают y max .
Определение 4 . Точку x 0 называют точкой минимума функции y f x , если для всех x из ее окрестности справедливо неравенство f x 0 f x . Значение функции в точке минимума называют минимумом функции и обозначают y min .
! Под окрестностью точки x 0 понимают интервал x 0 ; x 0 , где – достаточно малое положительное число.
Определение 5 . Точки минимума и максимума называют точками экстремума , а значения функции, соответствующие точкам экстремума, называют экстремумами функции .
Тема: «Исследование функции»
. Следует различать экстремумы функции и наибольшее-наименьшее значения функции. На 1-м рисунке наибольшее значение функции на отрезке a ; b достигается в точке максимума и равно максимуму функции , а на 2-м рисунке – наибольшее значение функции достигается в точке x b ,
которая не является точкой максимума .
Необходимое условие существования локальных экстремумов
Пусть точка x 0 является точкой экстремума функции f x , определенной в некоторой
окрестности точки x 0 . Тогда либо производная
не существует, либо
Достаточные условия существования локальных экстремумов
Первое достаточное условие
Пусть функция y f x непрерывна в окрестности точки x 0
и существуют конечные или
бесконечные односторонние производные f
x . Тогда при условии f
0, x 0 является точкой строгого локального максимума . А если
является точкой строгого локального минимума .
! Заметим, что при этом функция не дифференцируема в точке x 0.
Тема: «Исследование функции»
Второе достаточное условие
Пусть функция f x непрерывна и дважды дифференцируема в точке x 0. Тогда при условии
0, x 0 является точкой локального максимума . А если
0, то x 0 является точкой локального минимума .
Алгоритм определения точек экстремума (на базе 1-го достаточного условия)
1. Находим область определения функции.
2. Находим 1-ю производную функции на области определения.
3. Определяем нули числителя, нули знаменателя 1-й производной и точки области определения, в которых 1-я производная не существует (эти точки называют точками возможного экстремума или стационарными точками , проходя через эти точки, производная может изменять свой знак).
4. Стационарные точки разбивают область определения функции на промежутки монотонности , в которых производная сохраняет знак.
5. Определяем знаки 1-й производной на каждом из интервалов (например, вычисляя значение производной функции в любой точке отдельно взятого интервала).
6. Выбираем точки, в которых функция непрерывна и, проходя через которые, производная меняет знак.
Алгоритм определения точек экстремума (на базе 2-го достаточного условия)
1. Находим область определения функции.
2. Находим 1-ю производную функции на области определения.
3. Определяем нули числителя (эти точки называют точками возможного экстремума или
4. Находим 2-ю производную функции на области определения.
5. Определяем знак 2-й производной в стационарных точках.
6. Делаем вывод о типе экстремума по знаку 2-й производной.
Третье достаточное условие
Пусть функция f x имеет производные до n -ого порядка в – окрестности точки x 0 и
производные до n+ 1-ого порядка в самой точке x 0 .
если n – четное, то x 0 – точка перегиба (см. дальше) ;
если n – нечетное, то x 0 – точка экстремума ;
Исследование функции на выпуклость-вогнутость. Точки перегиба.
Определение 6 . Дифференцируемая функция называется выпуклой вниз на интервале Х , если ее график расположен не ниже касательной к нему в любой точке интервала Х .
Определение 7 . Дифференцируемая функция называется выпуклой вверх на интервале Х , если ее график расположен не выше касательной к нему в любой точке интервала Х .
! Выпуклую вверх функцию часто называют выпуклой , а выпуклую вниз – вогнутой .
Тема: «Исследование функции»
Определение 8 . Точка M x 0 , f x 0 называется точкой перегиба графика функции y f x ,
если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу ) и существует такая окрестность точки x 0 , в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости.
. Точка М называется точкой перегиба графика функции, если в этой точке существует касательная и график функции меняет направление выпукл ости, проходя через нее.
Примеры точек перегиба (отмечены красными точками) .
. Некоторые функции могут не иметь точек перегиба, а другие могут иметь одну , нескольк о или бесконечно много точек перегиба.
Нахождение интервалов выпуклости функции
Если функция y f x имеет конечную вторую производную на интервале Х , и если выполняется неравенство f x 0, x X ( f x 0, x X ), то график функции имеет выпуклость направленную вниз ( вверх ) на Х .
! Для нахождения промежутков выпуклости и вогнутости функции необходимо решить неравенства f x 0 и f x 0 соответственно.
! Точки, в которых функция y f x определена , а вторая производная не существует , включаются в интервалы вогнутости и выпуклости.
Тема: «Исследование функции»
Необходимое и достаточные условия наличия точек перегиба
Необходимое условие перегиба графика функции
Пусть график функции y f x имеет перегиб в точке M x 0 , f x 0 и имеет при x x 0
непрерывную вторую производную, тогда выполняется равенство f x
. Из этого условия следует, что абсциссы точек перегиба следует искать среди тех точек, в которых вторая производная функции обращается в ноль . НО, это условие не является достаточным, то есть не все значения x 0 , в которых вторая производная равна нулю, являются абсциссами точек перегиба.
. По определению точки перегиба требуется существование касательной, можно и вертикальной. Это означает, что абсциссами точек перегиба могут быть все x 0 из области
определения функции, для которых lim f x и
lim f x . Обычно это точки, в
которых знаменатель первой производной обращается в ноль.
После того как найдены все x 0 , которые могут быть абсциссами точек перегиба, следует воспользоваться первым достаточным условием перегиба графика функции.
Первое достаточное условие перегиба графика функции
Пусть функция y f x непрерывна в точке M x 0 , f x 0 , имеет в ней касательную (можно вертикальную) и эта функция имеет вторую производную в некоторой окрестности точки x 0 .
Тогда, если в пределах этой окрестности слева и справа от x 0 , вторая производная имеет разные знаки, то M x 0 , f x 0 является точкой перегиба графика функции.
Первое достаточное условие не требует существования второй производной в самой точке x 0 , но требует ее существование в окрестности точки x 0 .
Алгоритм нахождения точек перегиба функции
1. Находим все абсциссы x 0 возможных точек перегиба графика функции.
2. Выясняем, проходя через какие точки x 0 оси абсцисс, вторая производная меняет знак. Эти значения и будут абсциссами точек перегиба, а соответствующие им точки M x 0 , f x 0
будут точками перегиба графика функции.
Второе достаточное условие перегиба графика функции
Если f x 0 0, а f x 0 0, тогда x 0 является абсциссой точки перегиба графика функции y f x .
Третье достаточное условие перегиба графика функции.
Пусть f x 0 f x 0 f x 0 f n x 0 0, а f n 1 x 0 0, тогда если
n – четное число, то x 0 является абсциссой точки перегиба графика функции y f x .
Ответ
Проверено экспертом
Найдем производную данной функции
и приравняем ее к нулю
На промежутке x ∈ (-∞;2) и x ∈ (4;+∞) функция возрастает, а убывает на промежутке x ∈ (2;4). В точке x = 2 функция имеет относительный максимум, а в точке x = 4 — относительный минимум.
Найдем вторую производную данной функции
На промежутке x ∈ (-∞ ;3) функция выпукла вверх, а на промежутке x ∈ (3; +∞) — выпукла вниз