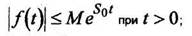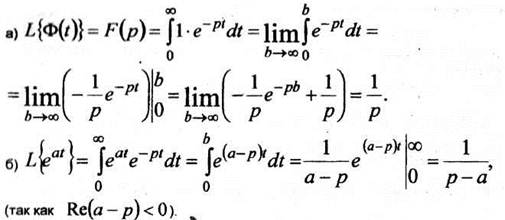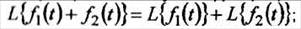Назначение . Данный сервис предназначен для нахождения онлайн оригинала f(t) по изображению F(p) . Результаты вычисления оформляются в формате Word (см. пример).
- Решение онлайн
- Видеоинструкция
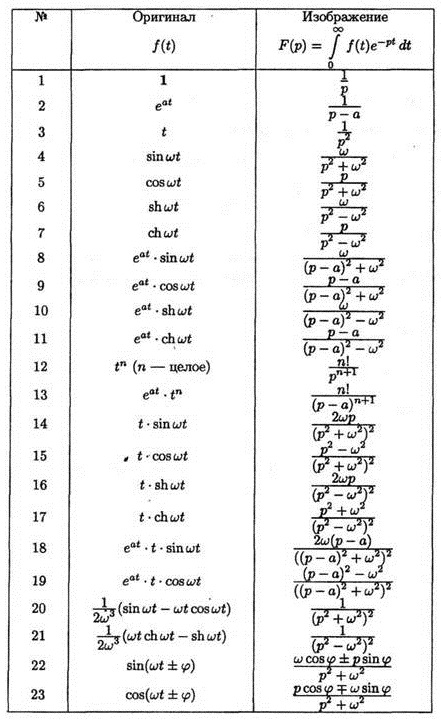
Таблица оригиналов и изображений Лапласа
| Изображение | Оригинал |
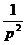 | t |
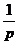 | 1 |
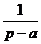 | e at |
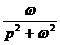 | sin(ωt) |
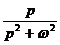 | cos(ωt) |
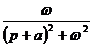 | e -at sin(ωt) |
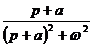 | e -at cos(ωt) |
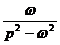 | sh(ωt) |
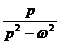 | ch(ωt) |
Начальной функцией или оригиналом называют функцию f(t) действительной переменной t , удовлетворяющей следующим условиям:
- f(t)=0 при t 0 и s – некоторые вещественные числа, то |f(t)|≤Me st при t≥0.
- f(t) — кусочно-непрерывная и интегрируемая на любом конечном отрезке изменения t .
Точная нижняя грань s0 всех чисел s , для которых выполняется неравенство, называется показателем роста функции f(t) .
Теоремы запаздывания и смещения
Теорема смещения: L[e p0t f(t)] = F(p-p0).
Пример . (p+4)/((p+4) 2 +9) = e -4t cos(3t)
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Содержание:
1. Функция оригинал и изображение по Лапласу
2. Теоремы преобразования Лапласа
3. Методы определения оригинала по известному изображению
4. Решение дифференциальных уравнений и систем операционным методом
5. Примеры решения задач
6. Вопросы и задачи для самостоятельной работы
Функцией- оригиналом — называют функцию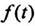 
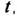
действительного аргумента
удовлетворяющую условиям:
1) для всех отрицательных значений аргумента функция тождественно равна нулю, т.е.
2) функция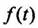 
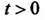
при 
возрастает не быстрее показательной
функции, т.е. существ.уют такие постоянные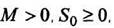 
что
3) на любом конечном отрезке положительной полуоси 
функция 
и ее производные достаточно высокого порядка непрерывны или имеют конечное число разрывов 1-го рода.
Простейшей функцией — оригиналом является единичная функция Хевисайда
(1)
Если функция 
не удовлетворяет условию 
то произведение 
уже ему удовлетворяет, т.е. будет оригиналом.
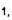
Для простоты записи множитель 
опускается, например, пишут вместо 
вместо 
и т.д.
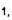
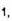
Изображением функции 
по Лапласу (преобразованием по Лапласу) называют функцию комплексной переменной 
определяемую соотношением
(2)
Интеграл (1.2) называют интегралом Лапласа.
Функция 
определяется в полуплоскости 
и является в этой области аналитической функцией.
То, что функция комплексной переменной 
является изображением по Лапласу функции действительного аргумента 
обозначается 
или
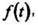
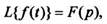
Изображение элементарных функций получается непосредственно с помощью интеграла (2).
Пример 1 Найти изображение по Лапласу функции 
Таким образом, получаем
Преобразование, основанное на интеграле Лапласа (2), обладает линейными свойсгыами.
1. Преобразование суммы функций равно сумме преобразований этих функций
2 Постоянный множитель можно выносить за знак преобразования:
Из этих двух свойств следует, что линейной комбинации оригиналов соответствует линейная комбинация их преобразований:
(3)
Пример 2. Найти изображение функции 
Используем формулу (2) для функции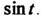 
Тогда
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8835 — 
| 7551 — 
или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Содержание
Преобразование Лапласа как разложение сигнала по системе затухающих комплексных экспонент
Ранее мы рассмотрели преобразование Фурье сигнала :
где — спектральная плотность сигнала , и — операторы прямого и обратного преобразования Фурье соответственно.
Условием существования преобразования Фурье является абсолютная интегрируемость [1] исходного сигнала сигнала , т.е. сходимость интеграла:
При рассмотрении преобразования Фурье предполагается, что время измеряется от минус бесконечности до плюс бесконечности. Кроме того (2) сужает класс сигналов, для которых существует преобразование Фурье.
С другой стороны, все физические процессы имеют начало, поэтому мы можем считать, что исходный сигнал определён на положительном интервале времени, т.е , при .
Для того, чтобы предотвратить расхождение интеграла (2) умножим входной сигнал на , где — вещественная величина. Рассмотрим преобразование Фурье полученного сигнала:
Очевидно, зависит от параметра . Тогда можно трактовать как функцию двух вещественных переменных или как функцию одной комплексной переменной . Обозначив получим:
Выражение (4) представляет собой разложение по системе затухающих комплексных экспонент , которое носит название преобразования Лапласа, где — оператор преобразования.
Исходный сигнал называют оригиналом, а — образом, или изображением оригинала.
Обратное преобразование Лапласа
Обратное преобразование Фурье (3) от имеет вид:
Умножим левую и правую части (5) на , получим:
Учтём, что , изменим переменную интегрирования с на :
При этом верхний и нижний пределы интегрирования равны:
Окончательно (6) с учётом 7 и (8):
Выражение (9) определяет обратное преобразование Лапласа, которое обозначается оператором .
Некоторые свойства преобразования Лапласа
Свойство линейности
Пусть сигнал . Тогда преобразование Лапласа :
Следствием (10) является умножение на константу:
Свойство подобия (масштабирование по аргументу)
Пусть сигнал имеет образ . Тогда изображение масштабированного во времени сигнала равно:
Аналогично можно показать [2], что масштабирование образа по аргументу приводит к оригиналу вида:
Преобразование Лапласа задержанного сигнала
Рассмотрим преобразование Лапласа сигнала , задержанного во времени на положительную величину .
Важно отметить, что (14) справедливо, если задержка положительна, как это показано на рисунке 1.
Рисунок 1. Пример положительной и отрицательной
Если же задержка отрицательна, то [2, стр. 40–41]:
Аналогичное свойство смещения образа:
Таким образом, смещение образа на произвольное комплексное приводит к умножению сигнала на .
Свойство дифференцирования оригинала и образа
Пусть дан сигнал и его преобразование Лапласа равно . Рассмотрим преобразование Лапласа производной сигнала :
Применяя правило интегрирования по частям [3, стр. 330]:
где — значение сигнала при . Если функция при имеет разрыв, то вместо необходимо брать правый предел :
при стремлении к нулю справа.
Таким образом, использование аппарата преобразования Лапласа позволяет заменить дифференцирование умножением образа на переменную . Это важнейшее свойство дало возможность перейти от дифференциальных уравнений при анализе цепей переменного тока к алгебраическим и использовать всю мощь аппарата операционного исчисления и теории функций комплексного переменного для синтеза и анализа электрических цепей.
Приведем также выражение для обратного преобразования Лапласа производной образа [4, стр. 224]. Пусть — образ сигнала . Тогда
где — производная -го порядка образа .
Свойство интегрирования оригинала и образа
Пусть сигнал есть результат интегрирования сигнала :
Рассмотрим преобразование Лапласа от :
Изменим порядок интегрирования и получим:
Получили еще одно важнейшее свойство: образ интеграла от входного сигнала равен образу этого сигнала, деленного на переменную . Это свойство также позволяет заменить интегральные уравнения и системы на алгебраические.
Преобразование Лапласа свертки двух сигналов
Пусть сигнал представляет собой свертку двух сигналов и , определяемую соотношением:
Важность интеграла свертки (24) в том, что им описывается результат прохождения сигнала через линейный фильтр с импульсной характеристикой .
Обратим внимание, что пределы интегрирования от 0 до обусловлены тем, что и отличны от нуля только для положительных значений переменной .
Рассмотрим преобразование Лапласа сигнала :
Поменяем местами операции интегрирования, и учтем свойство временного сдвига (14):
Таким образом, интеграл свертки заменяется произведением образов входного сигнала и образа импульсной характеристики фильтра .
Данное свойство также является очень важным, поскольку анализ многокаскадных фильтров заменяется простым произведением образов импульсных характеристик этих фильтров.
Выводы
В данном разделе мы рассмотрели преобразование Лапласа и его некоторые свойства.
Аппарат операционного исчисления является основным инструментом анализа электрических цепей переменного тока, ввиду возможности замены операций дифференцирования и интегрирования алгебраическим умножением и делением на переменную .
Подробнее использование преобразования Лапласа для анализа цепей переменного тока будет рассмотрено в следующем разделе.