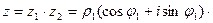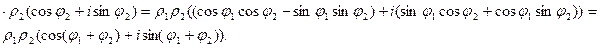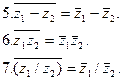Комплексные числа, их изображение на плоскости. Алгебраические операции над комплексными числами. Комплексное сопряжение. Модуль и аргумент комплексного числа. Алгебраическая и тригонометрическая формы комплексного числа. Корни из комплексных чисел. Показательная функция комплексного аргумента. Формула Эйлера. Показательная форма комплексного числа.
При изучении одного из основных приемов интегрирования: интегрирования рациональных дробей – требуется для проведения строгих доказательств рассматривать многочлены в комплексной области. Поэтому изучим предварительно некоторые свойства комплексных чисел и операций над ними.
Определение 7.1. Комплексным числом z называется упорядоченная пара действительных чисел (а,b) : z = (a,b) (термин «упорядоченная» означает, что в записи комплексного числа важен порядок чисел а и b: (a,b)≠(b,a) ). При этом первое число а называется действительной частью комплексного числа z и обозначается a = Re z, а второе число b называется мнимой частью z: b = Im z.
Определение 7.2. Два комплексных числа z1 = (a1 , b1) и z2 = (a2 , b2 ) равны тогда и только тогда, когда у них равны действительные и мнимые части, то есть a1 = a2, b1 = b2.
Действия над комплексными числами.
Замечание. Подмножеством множества комплексных чисел является множество действительных чисел, определяемых как комплексные числа вида (а,0). Можно убедиться, что при этом определение операций над комплексными числами сохраняет известные правила соответствующих операций над действительными числами. Кроме того, действительное число 1 = (1,0) сохраняет свое свойство при умножении на любое комплексное число: 1∙ z = z.
Определение 7.3. Комплексное число (0, b) называется чисто мнимым . В частности, число (0,1) называют мнимой единицейи обозначают символом i.
Свойства мнимой единицы:
1) i∙i=i² = -1; 2) чисто мнимое число (0,b) можно представить как произведение действительного числа (b,0) и i : (b,0) = b∙i.
Следовательно, любое комплексное число z = (a,b) можно представить в виде: (a,b) = (a,0) + (0,b) = a + ib.
Определение 7.4. Запись вида z = a + ib называют алгебраической формой записи комплексного числа.
Замечание. Алгебраическая запись комплексных чисел позволяет производить операции над ними по обычным правилам алгебры.
Определение 7.5. Комплексное число 
3. Вычитание комплексных чисел определяется как операция, обратная сложению: z =(a,b) называется разностью комплексных чисел z1 = (a1 , b1) и z2 = (a2 , b2 ), если a = a1 – a2 , b = b1 – b2.
4. Деление комплексных чисел определяется как операция, обратная умножению: число z = a + ib называется частным от деления z1 = a1 + ib1 и z2 = a2 + ib2 (z2 ≠ 0), если z1 = z∙z2. Следовательно, действительную и мнимую части частного можно найти из решения системы уравнений: a2 a – b2 b = a1 , b2 a + a2 b = b1.
Геометрическая интерпретация комплексных чисел.
Комплексное число z = (a,b) можно представить в виде точки на плоскости с координатами (a,b) или вектора с началом в начале координат и концом в точке (a,b).
При этом модуль полученного вектора называется модулем комплексного числа, а угол, образованный вектором с положительным направлением оси абсцисс,- аргументом числа. Учитывая, что a = ρ cos φ, b = ρ sin φ, где ρ = | z | — модуль z, а φ = arg z – его аргумент, можно получить еще одну форму записи комплексного числа:
Определение 7.6. Запись вида
называется тригонометрической формойзаписи комплексного числа.
В свою очередь, модуль и аргумент комплексного числа можно выразить через а и b: 
Легко убедиться, что операция сложения комплексных чисел соответствует операции сложения векторов. Рассмотрим геометрическую интерпретацию умножения. Пусть 
Следовательно, модуль произведения двух комплексных чисел равен произведению их модулей, а аргумент – сумме их аргументов. Соответственно, при делении модуль частного равен отношению модулей делимого и делителя, а аргумент – разности их аргументов.
Частным случаем операции умножения является возведение в степень:
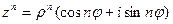
— формула Муавра.
Используя полученные соотношения, перечислим основные свойства комплексно сопряженных чисел:
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10077 — 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Для изображения комплексного числа на плоскости необходимо построить точку с координатами (x; y), где x и y соответственно равны действительной и мнимой частям
заданного комплексного числа. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Ось Ox называется действительной осью ,а ось Oy
— мнимой осью.
Пример 1. Изобразить на комплексной плоскости числа z1 = 1 — 3i, z2 = 4 + i, z3 = 5, найти их модули и аргументы.
Согласно теоретической сноске выше, имеем, что числу z1 = 1 — 3i соответствует точка с координатами (1; -3), z2 = 4 + i — точка (4; 1), а комплексному числу z3 = 5 соответствует точка с координатами (5; 0).
Комплексные числа можно отобразить просто точками, а можно сделать по-другому, как в данном примере, изобразить радиус-вектором точки с началом в точке О.
Длина этого вектора называется модулем числа z и обозначается |z|. По определению, модуль комплексного числа:
где x и y соответственно действительная и мнимая части комплексного числа.
Найдем модули и аргументы для каждого заданного числа (см. рисунок)
Пример 2. Найти и построить на комплексной плоскости области, которым принадлежат точки z = x + i y, удовлетворяющие условию 2 ≤ Re(z + 1) ≤ 4.
Преобразуем заданное неравенство: 2 ≤ Re(x + 1 + iy) ≤ 4.
Поскольку выражение Re (x + 1 + iy) определяет действительную часть числа, записанного в скобках, то можно перейти к следующему неравенству: 2 ≤ x + 1 ≤ 4. Или: 1 ≤ x ≤ 3.
Таким образом, условие 2 ≤ Re(z + 1) ≤ 4 определяет на комплексной плоскости область, множество точек (x; y) которой, удовлетворяют системе:
В математике кроме натуральных, рациональных и вещественных чисел имеется ещё один вид, называемый комплексными числами. Такое множество принято обозначать символом $ mathbb
Рассмотрим, что из себя представляет комплексное число. Запишем его таким образом: $ z = a + ib $, в котором мнимая единица $ i = sqrt <-1>$, числа $ a,b in mathbb
$ вещественные.
Если положить $ b = 0 $, то комплексное число превращается в вещественное. Таким образом, можно сделать вывод, что действительные числа это частный случай комплексных и записать это в виде подмножества $ mathbb
Принято записывать мнимую часть комплексного числа как $ Im(z) = b $, а действительную $ Re(z) = a $.
Введем понятие комплексно-сопряженных чисел. К каждому комплексному числу $ z = a+ib $ существует такое, что $ overline
= a-ib $, которое и называется сопряженным. Такие числа отличаются друг от друга только знаками между действительной и мнимой частью.
Формы
Так сложилось в математике, что у данных чисел несколько форм. Число одно и тоже, но записать его можно по-разному:
- Алгебраическая $ z = a+ib $
- Показательная $ z = |z|e^ $
- Тригонометрическая $ z = |z|cdot(cos(varphi)+isin(varphi)) $
Далее с примерами решений вы узнаете как переводить комплексные числа из одной формы в другую путем несложных действий в обе стороны.
Изображение
Изучение выше мы начали с алгебраической формы. Так как она является основополагающей. Чтобы было понятно в этой же форме изобразим комплексное число на плоскости:
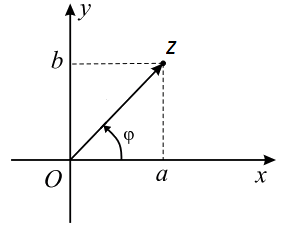
Комплексное число $ z = a+ib $ представляется в виде вектора $ overline
Аргумент обозначается $ varphi $.
Модуль $ |z| $ равняется длине вектора $ overline
Аргумент комплексного числа $ varphi $ нужно находить по различным формулам в зависимости от полуплоскости, в которой лежит само число.
| Пример 2 |
| Решение |
| Ответ |
| $$ z_1 + z_2 = 8 — i; z_1 — z_2 = -2 + 3i $$ |
| Пример 3 |
| Решение |
| Ответ |
| $$ z_1 cdot z_2 = 17 — i; frac |
| Пример 4 |
| Возвести комплексное число $ z = 3+3i $ в степень: a) $ n=2 $ б) $ n=7 $ |
| Решение |
| Ответ |
| Пример 5 |
| Извлечь корень $ sqrt[3] <-1>$ над множеством $ mathbb |
| Решение |
| Ответ |
| Пример 6 |
| Решить квадратное уравнение $ x^2 + 2x + 2 = 0 $ над $ mathbb |
| Решение |