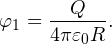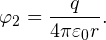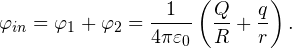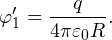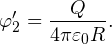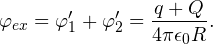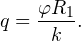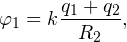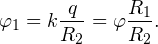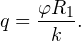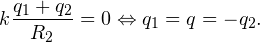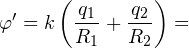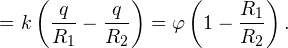При внесении незаряженного проводника во внешнее электрическое поле свободные заряды начинают двигаться и через небольшое время приходят в равновесие. Создается стационарное распределение зарядов, при котором на одной стороне проводника образуется избыток отрицательных зарядов, а на другой — избыток положительных. Это явление называется электростатической индукцией (рис. 2.5).
Рис. 2.5. Электростатическая индукция
Поле индуцированных (появившихся на поверхности проводника) зарядов полностью компенсирует внутри проводника внешнее поле. В противном случае внутри проводника происходило бы движение электрических зарядов, и распределение не было бы стационарным. Итак, при равновесном состоянии суммарное поле (внешнее и индуцированных зарядов) внутри проводника равно нулю. Поэтому в отношении суммарного поля справедливы выводы, сделанные нами ранее для заряженных проводников в отсутствии внешнего поля.
В частности, электрическое поле будет отсутствовать во внутренней полости в материале проводника (рис. 2.6). На свойстве проводников экранировать внешние поля (не пропускать их внутрь области, окруженной проводником) основывается электростатическая защита от действия внешних электростатических полей (рис. 2.7).
Рис. 2.6. Появление индуцированных зарядов на поверхности проводника
при воздействии на него внешнего электрического поля
Рис. 2.7. Электростатическая защита. Поле в металлической полости равно нулю
Так, автомобиль является безопасным убежищем во время грозы, и не потому, что резина на колесах изолирует его от земли. Здесь мы должны быть благодарны теореме Остроградского — Гаусса. Однако следует подчеркнуть, что замкнутый полый проводник экранирует полость внутри себя только от внешних зарядов и полей. Если внести заряды внутрь полости, то там появится электрическое поле при том, что в самом проводнике поле, по-прежнему будет равно нулю.
Далее, суммарное поле вблизи проводника перпендикулярно его поверхности и равно
где 
На практике приходится решать следующую задачу. Дано некоторое внешнее поле. В него вносится проводник заданной формы. Надо найти распределение индуцированных на нем зарядов и те изменения суммарного поля вне проводника, к которым они приводят. Плотность зарядов при заданном потенциале проводника определяется кривизной поверхности: 
Рис. 2.8. Электрическое поле (силовые линии и эквипотенциальные поверхности)
незаряженной сферы вблизи точечного электрического заряда
Задача. Дана сферическая металлическая оболочка с внутренним и внешним радиусами 


Рис. 2.9. Электрическое поле положительного заряда 
Решение. Благодаря сферической симметрии заряды расположатся на поверхностях оболочки с постоянной поверхностной плотностью: 



















Нам осталось найти потенциал поля в различных точках системы. Вне оболочки потенциал совпадает с потенциалом точечного заряда: 




Получаем в итоге:
Графики зависимости напряженности поля и потенциала представлены на рис. 2.10.
Рис. 2.10. Напряженность и потенциал электрического поля заряда q,
окруженного металлической оболочкой с внутренним радиусом 

Пунктирные линии соответствуют характеристикам поля одиночного заряда в отсутствие оболочки
Дополнительная информация
Металлический шар радиусом a помещён в металлическую сферическую оболочку, внутренний радиус которой R1, а внешний — R2. Центры шара и оболочки сов-падают. Заряд шара равен q>0 , оболочки — Q . Как зависят напряжённость и потенциал поля, создаваемого шаром и оболочкой, от расстояния r от центра системы? Нарисовать графики Е = Е(r) и ц(r).
Среди школьных задач по физике особняком стоят те, которые связаны с концентрическими проводящими сферами. Эти сферы могут быть заряжены, заземлены, могут находиться в поле внешних зарядов и т. д., вариаций много. В школьном курсе физики эти задачи являются одними из самых сложных. Не в последнюю очередь, конечно, непонимание данного материала связано с неспособностью учителей объяснить его грамотно и доступно. Итак, попробуем разобраться, что это за проводящие сферы и с чем их едят.
Тексты заданий я взял из сборника задач по физике для подготовительных отделений вузов.
| Задача 1. Сфера радиуса r, которой сообщен заряд q, окружена концентрической тонкостенной проводящей сферической оболочкой радиуса R, заряд которой равен Q. Определите потенциалы сфер φin (внутренней) и φex (внешней). |
Решение. Потенциал на поверхности внутренней сферы φex складывается из двух потенциалов: внешней сферы φ1 и собственно внутренней сферы φ2.
Потенциал внешней сферы φ1 в каждой точке ее внутреннего объема одинаков и равен потенциалу на ее поверхности (подробнее о решении задач на тему «Потенциал» читайте в этой статье):
Потенциал внутренней сферы φ2 определяется известным соотношением:
Тогда общий потенциал φin на поверхности внутренней сферы равен:
Потенциал на поверхности внешней сферы также складывается из двух потенциалов: внутренней сферы φ’1 и собственно внешней сферы φ’2.
Потенциал внутренней сферы φ’1 на расстоянии R от ее центра определяется известным соотношением:
Формула, определяющая потенциал внешней сферы φ’2 на ее поверхности, также хорошо известна:
Тогда общий потенциал на поверхности внешней сферы равен:
| Задача 2. Металлический шар радиуса R1, заряженный до потенциала φ, окружают тонкой сферической проводящей оболочкой радиуса R2. Определите потенциал шара φ1 после того, как он будет соединен проводником с оболочкой. Первоначальный заряд оболочки равен нулю, центры оболочки и шара совпадают. |
Решение. До соединения сфер проводником заряд первой был равен:
После соединения часть заряда с внутренней сферы перетекло на внешнюю. Ток прекратился в тот момент, когда потенциал шара стал равен потенциалу внешней оболочки. Удобнее поэтому искать не потенциал шара, а равный ему потенциал внешней оболочки. В соответствии с результатами, полученными в предыдущей задаче, этот потенциал определяется выражением:
где q1 и q2 — заряды шара и внешней оболочки после соединения их проводником соответственно. По закону сохранения заряда q = q1 + q2. После несложных преобразований получаем:
| Задача 3. Металлический шар радиуса R1, заряженный до потенциала φ, окружают концентрической сферической проводящей оболочкой радиуса R2. Чему станет равен потенциал шара φ‘, если заземлить оболочку? |
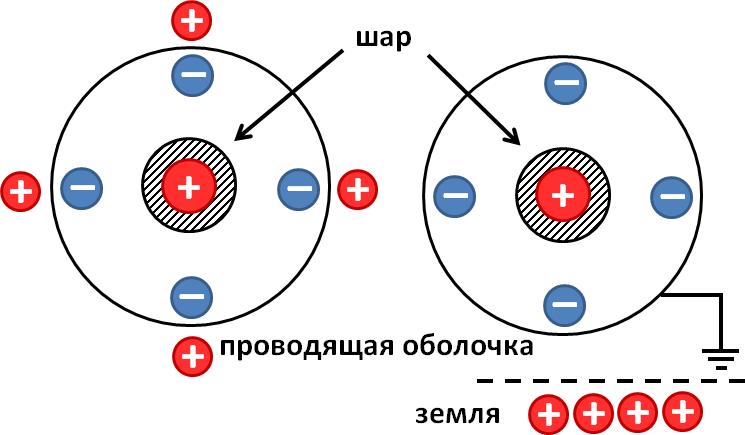
Начнем с рисунка к решению задачи:
После заземления проводящей оболочки весь положительный заряд, образовавшийся на ней вследствие явления электростатической индукции, стекает на землю. На ней остается только отрицательный заряд, поскольку он притягивается к положительному заряду внутренней сферы
Решение. Зная потенциал шара в начальный момент времени и его радиус, можно найти заряд на нем:
Вследствие явления электростатической индукции на внешней оболочке должно произойти разделение заряда. Отрицательный заряд перетечет на внутреннюю поверхность оболочки, положительный — на внешнюю (см. рисунок). Это же явление возникало и в предыдущих задачах, но мы не принимали его во внимание. Почему? В условии задач было указано, что оболочка тонкая, и такое «разбегание» зарядов не приводило к сколько-нибудь существенному изменению конфигурации электростатического поля.
В этой задаче учет данного явления важен, поскольку оболочку заземляют. После заземления положительный заряд с оболочки стечет на землю, останется лишь отрицательный q2, поскольку он притягивается к положительному заряду q1 внутренней сферы. Потенциал заземленной оболочки станет равен потенциалу земли, то есть нулю. В этой связи и в соответствии с результатом, полученным при решении первой задачи, получаем равенство:
Используя выражение для расчета потенциала внутренней сферы подобной системы, полученное в первой задаче, находим окончательно требуемый потенциал шара:
Опыт показывает, что редко кто понимает решение этих задач во всех деталях с первого раза. Обычно приходится долго и настойчиво разъяснять ученикам все те мелочи, без осознания которых решение сводится к пустым преобразованиям буквенных выражений с целью получения приведенного в конце учебника ответа. Понять физическую сущность этих задач и научиться применять полученные знания в будущем не просто. Однако в этом и состоит основная методическая ценность данной темы в школьном курсе физики. Лучшим помощником в ее изучении непременно станет профессиональный репетитор, грамотный наставник, который сможет придумать понятное именно вам объяснение и ответит на все возникшие вопросы. Кстати, если таковые имеются, вы можете задать их ниже в комментариях.