Формула. Объём шара:

V =4π R 3 =1π D 3
36

S = 4 π R 2 = π D 2

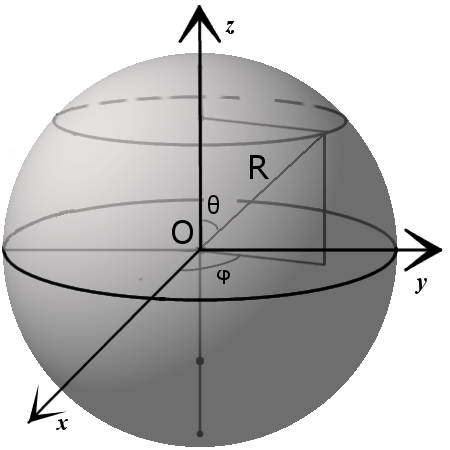
Уравнение сферы

x 2 + y 2 + z 2 = R 2

( x — x 0) 2 + ( y — y 0) 2 + ( z — z 0) 2 = R 2

Основные свойства сферы и шара

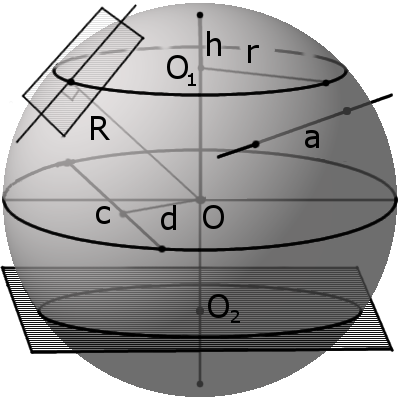
Секущая, хорда, секущая плоскость сферы и их свойства

d m между секущей плоскостью и центром сферы всегда меньше радиуса R:

m r такого круга можно найти по формуле:

где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.

Касательная, касательная плоскость к сфере и их свойства

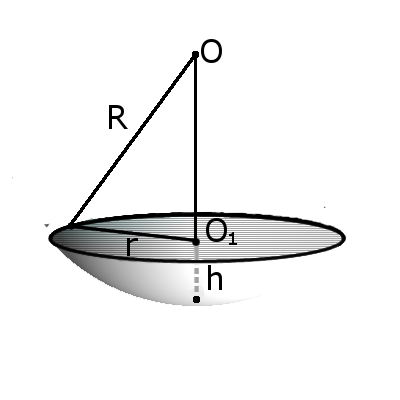
Формула. Объём сегмента сферы с высотой h через радиус сферы R:

V =h 2 π(3R — h )
3

S = π R(2 h + √ 2 h R — h 2 )

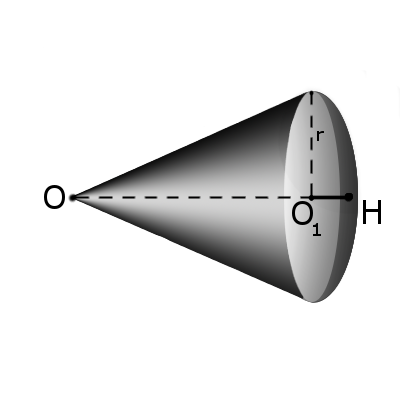
Формула. Объём сектора V с высотой O1H (h) через радиус шара OH (R):

V =2 π R 2 h
3

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Шаровой ( сферической ) – другими словами границей шара – поверхностью является геометрическое место точек (т.е. множество всех точек) в пространстве, которые равноудалены от одной точки O , называющейся центром сферической поверхности .

Понятие шара в метрическом пространстве естественным образом обобщает понятие шара в евклидовой геометрии.

Т.о., точками сферы оказывается каждая точка шара, которая удалена от центра на расстояние, которое равно радиусу. Каждый отрезок, который соединяет центр шара и точку на шаровой поверхности, тоже называют радиусом .

Отрезок, который соединяет 2 точки шаровой поверхности и который проходит сквозь центр шара, называется диаметр . Любой диаметр соответствует 2-м радиусам. Концы всякого диаметра называются диаметрально противоположными точками шара.

Эта точка О называется центром сферы , а расстояние AO , в свою очередь, называется радиусом сферы .

Радиус AO и диаметр AB находят тем же способом, что и для окружности.

Сфера является поверхностью (границей) шара с центром и радиусом, как у сферы.

Шар — это тело правильно геометрической формы, ограниченное поверхностью шара. Шар возможно получить, методом вращения полукруга/круга около диаметра.

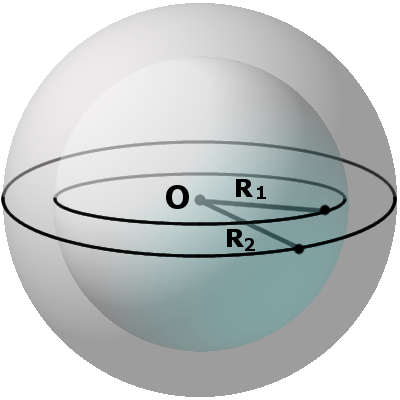
Любое плоское сечение шара является кругом. Чем ближе секущая плоскость к центру шара, тем радиус круга становится больше. Самый большой круг оказывается при прохождении плоскости через центр O. Этот круг разделяет шар на две равные части и он называется большим кругом. Радиус большого круга равен радиусу шара.

Меридианы шара (сферы).

Сквозь 2 точки шара, которые лежат на концах общего диаметра, возможно провести бесконечное число больших кругов — меридианов. Через 2 точки, которые не на концах общего диаметра шара возможно провести всего лишь 1 большой круг.

Основные геометрические формулы шара (сферы).

Площадь поверхности S и объём V шара радиуса r, диаметра d можно определить по формулам:

Определения, связанные с понятием шара.

Предположим, дано метрическое пространство (X, ρ). Значит:

  • Шаром (или открытым шаром) с центром в точке и радиусом r>0 будет называться

Замкнутый шар с центром в x0 и радиусом r можно выразить так:

Свойства шара.

  • Шар – это открытое множеством в топологии, порождённой метрикой ρ.
  • Замкнутый шар — замкнутое множество в топологии, порождённой метрикой ρ.
  • По определению этой топологии открытые шары с центрами в любой точке X представляют собой её базу.
  • Т.е., . Но замыкание открытого шара не всегда совпадает с замкнутым шаром:
  • Например: допустим (X, ρ) — дискретное метрическое пространство, и X состоит из более, чем 2-х точек. Значит, для всякого будет:

  • Объём шара в 1,5 раз меньше, чем объём описанного вокруг этого шара цилиндра, а поверхность шара в 1,5 раз меньше полной поверхности этого цилиндра:

Sцил и Vцил – полная поверхность и объём описанного цилиндра вокруг шара.

Части шара.

Часть шара (сферы), которая отсекается от него любой плоскостью (ABC), является шаровым (сферическим) сегментом . Круг ABC является основанием шарового сегмента. О трезок MN перпендикуляра, который проведен из центра N круга ABC до пересечения со сферической поверхностью, является высотой шарового сегмента. Точка M является вершиной шарового сегмента.

Часть сферы, которая заключена между 2-мя плоскостями, которые параллельны ABC и DEF, которые пересекают сферическую поверхность, является шаровым слоем . Кривая поверхность шарового слоя является шаровым поясом . Круги ABC и DEF – основания шарового пояса . Расстояние NK между основаниями шарового пояса – его высота . Часть шара, которая ограничена кривой поверхностью сферического сегмента (AMCB) и конической поверхностью OABC , основанием у нее является основание сегмента (ABC) , а вершиной – центр шара O , называется шаровым сектором.

Формулу объёма шара можно объяснить следующими рассуждениями. В шаре возможно разместить огромное количество пирамид с очень маленькими основаниями, разместив пирамиды таким образом, чтобы их вершины располагались в центре шара, а основания лежали бы на поверхности шара и эти пирамиды соприкасались бы боковыми гранями.

Высота любой построенной пирамиды приблизительно равна радиусу (R) шара. Если не обращать внимание различиями этих длин, то объём (v) всех пирамид отдельно можно представить такой формулой:

Значит, сумма объёмов (V’) пирамид выразим формулой:

Сумма (S’) очень близка к площади поверхности шара (S).

Сумма объёмов всех пирамид (V’) приблизительно равна объёму (V) шара. Если не обращать внимание на незначительные различия в этих величинах, тогда получится такая формула:

которая показывает, что объём шара соответствует 1/3 произведения площади поверхности шара на длину радиуса. Зачастую озвучивают так: объём шара равен 1/3 произведения поверхности шара на его радиус.

Используя выражение S = 4πR 2 , вывели формулу:

где D — диаметр шара.

Примечание. В формуле V = 1/3 SR поставлен знак точного, а не приближённого равенства, хотя на основании проведённых рассуждений можно было принять его приближённым, хотя в старших классах средней школы доказываем, что равенство V = 1/3 SR точное, а не приближённое.

Построение точек на поверхности шара в ортогональных проекциях и аксонометрии вы­полняют с помощью параллелей, проведенных через заданные точки. Рассмотрим это на рис. 275. Точка А задана фронтальной про­екцией как видимая. Для построения ее гори­зонтальной проекции через фронтальную проек­цию а’ точки А проводят фронтальную проекцию параллели. Затем строят горизонтальную проек­цию этой параллели. Для этого радиусом, рав­ным расстоянию от вертикальной центровой ли­нии до точки, в которой фронтальная проекция параллели пересекает очерковую линию шара, проводят окружность. Точка А лежит в верхней части видимой половины шара, значит, ее горизонтальной проекция будет видимой и находит­ся ниже центровой линии 1 2 впересечении го­ризонтальной проекции параллели’ с линией проекционной связи, проведенной от точки а’. На фронтальной проекции видимой является та половина шара, которая на горизонтальной проекции располагается ниже центровой линии 12. А на горизонтальной проекции видимой будет та половина шара, которая на фронтальной проекции расположена выше центровой линии 1׳2′. Профильную проекцию а" точки А строят с помощью линий проек­ционной связи, проведенных с фронтальной проекции от точки а‘ и с горизонтальной проекции от точки а. На профильной проекции видимой будет та половина шара, которая на фронтальной и горизонтальной проекциях находится слева от вертикальной центровой линии. Именно в этой половине шара и распо­ложена точка А. Значит, она будет видимой.

Точка В задана горизонтальной проекцией, которая лежит на горизонтальной проекции экватора (см. рис. 275). Для построения точек b’ и b" достаточно с горизонтальной проекции b на фронтальную и профильную проекции провести линии проекционной связи до пересечения с проекциями экватора в точках b’ и b׳׳. Точка В будет видимой на всех проекциях.

Точка С, которая лежит на профильном ме­ридиане, задана профильной проекцией, (см, рис. 275). Профильный меридиан на фронталь­ной и горизонтальной проекциях шара изобра­жается как отрезок прямой линии, совпадаю­щей с вертикальной центровой линией, поэтому достаточно провести линии проекционной связи от точки с" до центровых линий, чтобы получить точки с и с’. На горизонтальной проекции часть профильного меридиана, где лежит точка с, будет видимой, так как точка С лежит в верхней части шара, видимой на горизонтальной про­екции. Значит, горизонтальная проекция с точки С будет видимой. Фронтальная проекция с’ точки С будет невидимой, так как располо­жена на профильной проекции в левой поло­вине проекции шара, а на горизонтальной проекции — в верхней половине, а эта полови­на шара на фронтальной проекции невидимая.

При построении точек, лежащих на поверхно­сти шара, в аксонометрии сначала строятся в плоскости экватора вторичные горизонталь­ные проекции точек Л и С nq координатам X и У, взятым с горизонтальной проекции. На рис. 275 это размеры m, n, k и d. Параллельно оси Qz от вторичных проекций точек Л и С в аксонометрии откладывают расстояния по высоте, взятые с фронтальной или профильной проекции. Так как точка В лежит на экваторе, то она строится по координате X, взятой , с горизонтальной проекции.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась — это был конец пары: "Что-то тут концом пахнет". 8409 — | 8023 — или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно