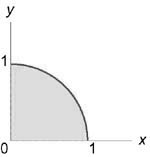
Объем тела V находится по формулам: 


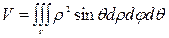
Пример 8.1. Найти объем тела, ограниченного поверхностями: z = x 2 + y 2 и z = 1. Сделать чертеж.
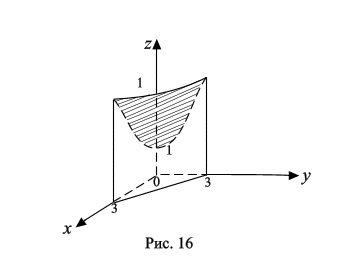
Решение. Данное тело ограничено сверху плоскостью z = 1, снизу –– параболоидом z = x 2 + y 2 (рис. 15). Объем тела находим, используя цилиндрические координаты:
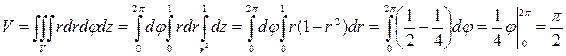
Пример 8.2. Найти объем тела, ограниченного поверхностями:
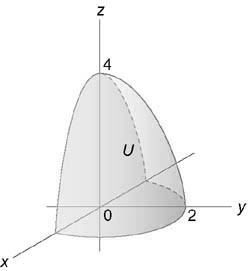
z = 4x 2 + 2y 2 + 1, x + y – 3 = 0, x = 0, y = 0, z = 0. Сделать чертеж.
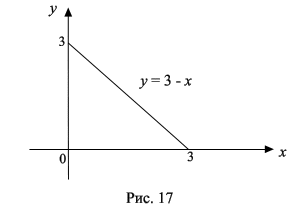
Решение. Данное тело ограничено сверху частью параболоида z = 4x 2 + 2y 2 + 1, снизу –– плоскостью z = 0, боковые поверхности: x = 0, y = 0 x + y = 3 (рис. 16). Проекцией тела на плоскость xOy есть треугольник (рис. 17).


Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Сдача сессии и защита диплома — страшная бессонница, которая потом кажется страшным сном. 8796 — 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
В этом разделе вы найдете подробные решения, связанные и вычислением и применением тройных интегралов: от непосредственного вычисления (в декартовых, цилиндрических, сферических координатах), до применения к нахождению объемов тел, массы, моментов и т.п. Примеры сгруппированы по темам:
Тройные интегралы: примеры решений
Задача 1. Вычислить тройной интеграл
$$iiint_V x^2yz dx dy dz, quad V: -1 le x le 2, 0le y le 3, 2 le z le 3. $$
Задача 2. Переходя к сферическим координатам, вычислить интеграл
$$iiint_V x^2 dxdydz, quad V: x^2+y^2+z^2=R^2,, zge 0, xgt 0.$$
Задача 3. Переходя к цилиндрическим координатам вычислить интеграл
$$iiint_V x^2 dxdydz, quad V: x^2+y^2=x,, z=x^2+y^2, z=0.$$
Задача 4. Решить тройной интеграл двумя способами (цилидрическая и сферическая замена координат)
Трудности с задачами? МатБюро поможет с интегралами.
Объемы тел: примеры решений
Задача 5. Найти объем тела, заданного ограничивающими его поверхностями (внутри цилиндра).
Задача 6. Найти объем тела, ограниченного поверхностями
Задача 7. Вычислить тройным интегрированием объем тела, ограниченного данными поверхностями:
Задача 8. Найти объем тела, ограниченного координатными плоскостями и поверхностью
Задача 9. Найти объем тела, ограниченного поверхностью $x^2+y^2+z^2=2x+3y$.
Моменты, масса тела: примеры решений
Задача 10. Найти статический момент относительно $xOy$ однородного тела, ограниченного поверхностью $$(x^2+y^2+z^2 )^3=frac $$ с плотностью $z=0$ $(z ge 0)$.
Задача 11. Используя тройной интеграл в цилиндрической системе координат, вычислить массу кругового цилиндра, нижнее основание которого лежит в плоскости $xOy$, а ось симметрии совпадает с осью $Oz$, если заданы радиус основания $R$, высота цилиндра $H$ и функция плотности $gamma(
ho)$, где $
ho$ – полярный радиус точки.
Задача 12. Найти массу тела, заданного системой неравенств, если плотность тела в каждой точке задана функцией $mu$.
Задача 13. Найти момент инерции относительно оси Oz тела, ограниченного заданными поверхностями.
Примеры применения цилиндрических и сферических координат
- Услуги проектирования
- Тройной интеграл
- Примеры применения цилиндрических и сферических координат
Как и в случае перехода к полярным координатам в двойном интеграле, дать однозначный рецепт того, когда следует применять цилиндрические или сферические координаты, нельзя, это дело опыта. Можно попробовать применить цилиндрические координаты, если подынтегральная функция и/или уравнения поверхностей, ограничивающих объём $mathbf < extit < V >> $, зависят от комбинации $mathbf < extit < x >> ^ < 2 >+mathbf < extit < y >> ^ < 2 >=mathbf < extit < r >> ^ < 2 >$; сферические — если эти уравнения зависят от $mathbf < extit < x >> ^ < 2 >+mathbf < extit < y >> ^ < 2 >+mathbf < extit < z >> ^ < 2 >=mathbf < extit < r >> ^ < 2 >$. Рассмотрим ряд примеров.
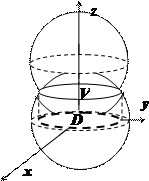
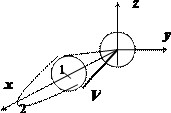
Найти объём $mathbf < extit < V >> $ общей части двух шаров, ограниченных сферами
Решение:
Пересечение сфер находится на уровне $2Rz=R^2Rightarrow z=R/2$ и представляет собой круг радиуса $Rfrac < sqrt 3 > < 2 >$. Объём $mathbf < extit < V >> $ограничен сверху поверхностью $z=sqrt < R^2-x^2-y^2 >$, снизу — поверхностью $z=R-sqrt < R^2-x^2-y^2 >$. Вычисления в декартовых координатах дают $V=iiintlimits_V < dv >=iiintlimits_V < dxdydz >=intlimits_ < -Rfrac < sqrt 3 > < 2 >> ^ < Rfrac < sqrt 3 > < 2 >> < dxintlimits_ < -sqrt < frac < 3 > < 4 >R^2-x^2 > > ^ < sqrt < frac < 3 > < 4 >R^2-x^2 > > < dyintlimits_ < R-sqrt < R^2-x^2-y^2 >> ^ < sqrt < R^2-x^2-y^2 >> < dz >> > $ — достаточно громоздкие выкладки.
В цилиндрических координатах объём $mathbf < extit < V >> $ ограничен сверху поверхностью $z=sqrt < R^2-r^2 >$, снизу — поверхностью $z=R-sqrt < R^2-r^2 >$, поэтому
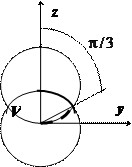
В сферических координатах уравнение нижней сферы принимает вид $r=R$, верхней — $r^2=2Rrcos heta Rightarrow r=2Rcos heta $, их пересечение соответствует значению $cos heta =1/2Rightarrow heta =pi /3$. В интервале $0leqslant heta leqslant pi /3 quad mathbf < extit < r >> $ меняется от $0$ до $mathbf < extit < R >> $, в интервале $pi /3leqslant heta leqslant pi /2 quad mathbf < extit < r >> $ меняется от $0$ до $2Rcos heta $, поэтому
В этом примере трудоёмкость вычислений в цилиндрических и сферических координатах примерно одинакова.
Решение:
Параболоид и конус пересекаются в плоскости $x=2-x^2Rightarrow x=1$ по кругу радиуса 1. Осью симметрии объёма $mathbf < extit < V >> $ служит ось $mathbf < extit < Ох >> $, поэтому цилиндрические координаты вводим формулами $x=x,quad y=rcos varphi ,quad z=rsin varphi ; quad I=iiintlimits_V < (x+y+z)dxdydz >=iiintlimits_V < (x+rcos varphi +rsin varphi )rdxdrdvarphi >=intlimits_0^ < 2pi > < dvarphi intlimits_0^1 < rdrintlimits_r^ < 2-r^2 > < (x+rcos varphi +rsin varphi )dx >> > =$ $ =intlimits_0^ < 2pi > < dvarphi intlimits_0^1 < left. < frac < x^2 > < 2 >>
ight|_r^ < 2-r^2 >rdr > > +intlimits_0^ < 2pi > < (cos varphi +sin varphi )dvarphi intlimits_0^1 < left. x
ight|_r^ < 2-r^2 >r^2dr > > =pi intlimits_0^1 < left( < 4-5r^2+r^4 >
ight)dr > =frac < 38pi > < 15 >. $ Применение сферических координат в этом примере нецелесообразно < громоздкое уравнение для параболоида >.
Решение:
Здесь область интегрирования — шар радиуса 1/2, сдвинутый по оси $mathbf < extit < Оz >> $ на 1/2 единицы, подынтегральная функция зависит от выражения $mathbf < extit < x >> ^ < 2 >+mathbf < extit < y >> ^ < 2 >+mathbf < extit < z >> ^ < 2 >$, поэтому применим сферические координаты. Уравнение сферы $x^2+y^2+z^2=zRightarrow r^2=rcos heta Rightarrow r=cos heta left( < Rightarrow 0leqslant heta leqslant pi /2 >
ight)$ , поэтому $I=iiintlimits_V < sqrt < x^2+y^2+z^2 >dxdydz > =iiintlimits_V < rcdot r^2sin heta drdvarphi d heta >=intlimits_0^ < 2pi > < dvarphi intlimits_0^ < pi /2 > < sin heta d heta >intlimits_0^ < cos heta > < r^3dr >> =frac < 2pi > < 4 >intlimits_0^ < pi /2 >< left. < r^4 >
ight|_0^ < cos heta >sin heta d heta > = \ =frac < 2pi > < 4 >intlimits_0^ < pi /2 > < cos ^4 heta sin heta d heta >=-frac < 2pi > < 4cdot 5 >left. < cos ^5 heta >
ight|_0^ < pi /2 >=frac < pi > < 10 >$.
Вычислить объём тела, ограниченного поверхностью $left( < x^2+y^2+z^2 >
ight)^ < ,2 >=a^3z,;a=const>0$
Решение:
Здесь тоже для того, чтобы понять, как устроено тело, и найти его объём, надо перейти к сферическим координатам < на это указывает комбинация $mathbf < extit < x >> ^ < 2 >+mathbf < extit < y >> ^ < 2 >+mathbf < extit < z >> ^ < 2 >=mathbf < extit < r >> ^ < 2 >)$. Уравнение поверхности $left( < x^2+y^2+z^2 >
ight)^ < ,2 >=a^3zRightarrow r^4=a^3rcos vartheta Rightarrow r=asqrt[3] < cos vartheta >;left( < Rightarrow 0leqslant heta leqslant pi /2 >
ight)$. По этому уравнению поверхность построить уже можно; отсутствие координаты $varphi $ в уравнении показывает, что это — тело вращения вокруг оси $mathbf < extit < Oz >> $. Находим объём: $ V=iiintlimits_V < r^2sin heta drdvarphi d heta >=intlimits_0^ < 2pi > < dvarphi intlimits_0^ < pi /2 > < sin >> heta d heta intlimits_0^ < asqrt[3] < cos heta >> < r^2dr >=frac < 2pi > < 3 >intlimits_0^ < pi /2 >< left. < r^3 >
ight|_0^ < asqrt[3] < cos heta >> sin heta d heta = > $ $ =frac < 2pi a^3 > < 3 >intlimits_0^ < pi /2 > < cos heta sin heta d heta = >frac < pi a^3 > < 3 >. $
Вычислить интеграл $iiintlimits_U < left( < < x^4 >+ 2 < x^2 > < y^2 >+ < y^4 >>
ight)dxdydz > ,$ где область (U) ограничена поверхностью ( < x^2 >+ < y^2 >le 1) и плоскостями (z = 0,) (z = 1).
Решение:
Данный интеграл удобно вычислить в цилиндрических координатах. Проекция области интегрирования на плоскость (Oxy) представляет собой круг ( < x^2 >+ < y^2 >le 1) или (0 le
ho le 1).
Заметим, что подынтегральное выражение записывается в виде $ < left( < < x^4 >+ 2 < x^2 > < y^2 >+ < y^4 >>
ight) > = < < left( < < x^2 >+ < y^2 >>
ight)^2 > > = < < left( < <
ho ^2 >>
ight)^2 > = <
ho ^4 >> $
Тогда интеграл будет равен $I = intlimits_0^ < 2pi > < dvarphi >intlimits_0^1 < <
ho ^4 >
ho d
ho > intlimits_0^1 < dz >.$
Здесь во втором интеграле добавлен множитель (
ho) якобиан преобразования декартовых координат в цилиндрические. Все три интеграла по каждой из переменной не зависят друг от друга.
Вычислить интеграл $iiintlimits_U < left( < < x^2 >+ < y^2 >>
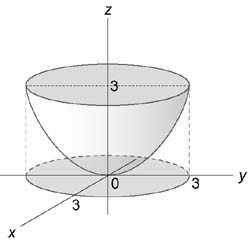
ight)dxdydz > ,$ где область (U) ограничена поверхностями ( < x^2 >+ < y^2 >= 3z,) (z = 3)
Решение:
Область интегрирования изображена на рисунке
Для вычисления интеграла перейдем к цилиндрическим координатам: $ < x =
ho cos varphi , >;; < y =
ho sin varphi , >;; < z = z. >$ Дифференциал при этом равен $dxdydz =
ho d
ho dvarphi dz;;left( <
ho — ext < якобиан >>
ight).$
Уравнение параболической поверхности принимает вид: $ <
ho ^2 > < cos ^2 >varphi + <
ho ^2 > < sin^2 >varphi = 3z;; ext < или >;; <
ho ^2 >= 3z.$ Проекция области интегрирования (U) на плоскость (Oxy) представляет собой окружность ( < x^2 >+ < y^2 >le 9) радиусом (
ho = 3).
Координата (
ho) изменяется в пределах от (0) до (3,) угол (varphi) от (0) до (2pi) и координата (z) от (largefrac < < <
ho ^2 >> > < 3 >
ormalsize) до (3.)
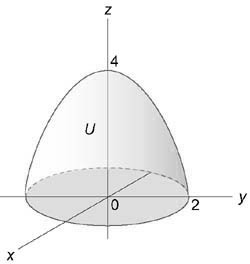
Используя цилиндрические координаты, найти значение интеграла $ I = intlimits_ < — 2 >^2 < dx >intlimits_ < — sqrt < 4 — < x^2 >> > ^ < sqrt < 4 — < x^2 >> > < dy >intlimits_0^ < 4 — < x^2 >- < y^2 >> < < y^2 >dz > $
Решение:
Область интегрирования (U) изображена на рисунке:
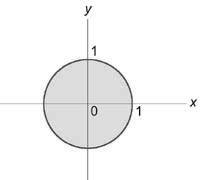
Ее проекция на плоскость (Oxy) представляет собой круг ( < x^2 >+ < y^2 >= < 2^2 >):
Новые переменные в цилиндрических координатах будут изменяться в пределах $ < 0 le
ho le 2, >;; < 0 le varphi le 2pi , >;; < 0 le z le 4 — <
ho ^2 >. > $
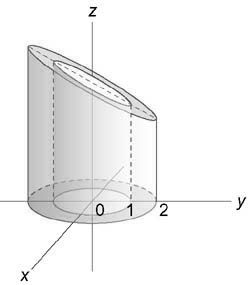
Вычислить интеграл, используя цилиндрические координаты: $iiintlimits_U < sqrt < < x^2 >+ < y^2 >> dxdydz > .$ Область (U) ограничена параболоидом (z = 4 — < x^2 >- < y^2 >,) цилиндром ( < x^2 >+ < y^2 >= 4) и плоскостями (y = 0,) (z = 0)
Решение:
Изобразив схематически область интегрирования (U,) находим, что ее проекция на плоскость (Oxy) < область (D) >представляет собой полукруг радиусом (
ho = 2).
Найти интеграл $iiintlimits_U < ydxdydz >,$ где область (U) ограничена плоскостями (z = x + 1,) (z = 0) и цилиндрическими поверхностями ( < x^2 >+ < y^2 >= 1,) ( < x^2 >+ < y^2 >= 4)
Решение:
Вычислим данный интеграл в цилиндрических координатах. Из условия $0 le z le x + 1$ следует, что $0 le z le
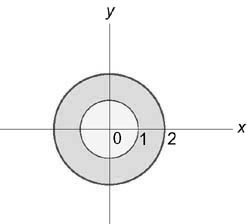
ho cos varphi + 1.$ Область интегрирования в плоскости (Oxy) представляет собой кольцо, ограниченное окружностями ( < x^2 >+ < y^2 >= 1) и ( < x^2 >+ < y^2 >= 4)
Следовательно, переменные (
ho) и (varphi) изменяются в интервале $1 le
ho le 2,;;0 le varphi le 2pi .$
Этот результат закономерен, поскольку область (U) симметрична относительно плоскости (Oxz,) а подынтегральная функция является четной.
Найти интеграл (iiintlimits_U < sqrt < < x^2 >+ < y^2 >+ < z^2 >> dxdydz > ,) где область интегрирования (U) шар, заданный уравнением ( < < x^2 >+ < y^2 >+ < z^2 >> = 25.)
Решение:
Поскольку область (U) представляет собой шар, и к тому же подынтегральное выражение является функцией, зависящей от $fleft( < < x^2 >+ < y^2 >+ < z^2 >>
ight),$ то перейдем к сферическим координатам.
Вычислить интеграл $iiintlimits_U < < e^ < < < left( < < x^2 >+ < y^2 >+ < z^2 >>
ight) > ^ < frac < 3 > < 2 >> > > > dxdydz > ,$ где область (U) представляет собой единичный шар ( < < x^2 >+ < y^2 >+ < z^2 >> le 1.)
Решение:
Центр данного шара расположен в начале координат. Следовательно, в сферических координатах область интегрирования (U) описывается неравенствами $ < 0 le
ho le 1, >;; < 0 le varphi le 2pi , >;; < 0 le heta le pi . >$
Как видно, тройной интеграл вырождается в произведение трех однократных интегралов, каждый из которых вычисляется независимо. В результате находим $ < I = intlimits_0^ < 2pi > < dvarphi >intlimits_0^1 < < e^ < <
ho ^3 >> > <
ho ^2 >d
ho > intlimits_0^pi < sin heta d heta >> = < left[ < left. varphi
ight|_0^ < 2pi >>
ight] cdot intlimits_0^1 < left( < < e^ < <
ho ^3 >> > cdot frac < 1 > < 3 >d <
ho ^3 >>
ight) > cdot left[ < left. < left( < — cos heta >
ight) >
ight|_0^pi >
ight] > = < 2pi cdot frac < 1 > < 3 >left[ < left. < left( < < e^ < <
ho ^3 >> > >
ight) >
ight|_ < <
ho ^3 >= 0 > ^ < <
ho ^3 >= 1 > >
ight] cdot left( < — cos pi + cos 0 >
ight) > = < frac < < 2pi >> < 3 >cdot left( < e — 1 >
ight) cdot 2 > = < frac < < 4pi >> < 3 >left( < e — 1 >
ight). > $
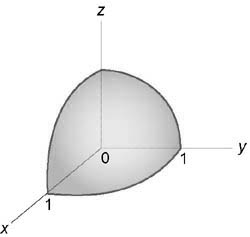
Вычислить интеграл (iiintlimits_U < xyzdxdydz >,) где область (U) представляет собой часть шара ( < x^2 >+ < y^2 >+ < z^2 >le < R^2 >,) расположенную в первом октанте (x ge 0, y ge 0, z ge 0.)
Решение:
Найти тройной интеграл $iiintlimits_U < left( < frac < < < x^2 >> > < < < a^2 >> > + frac < < < y^2 >> > < < < b^2 >> > + frac < < < z^2 >> > < < < c^2 >> > >
ight)dxdydz > ,$ где область (U) ограничена эллипсоидом $ < frac < < < x^2 >> > < < < a^2 >> > + frac < < < y^2 >> > < < < b^2 >> > + frac < < < z^2 >> > < < < c^2 >> > > = 1.$
Решение:
Для вычисления интеграла перейдем к обобщенным сферическим координатам путем следующей замены переменных: $ < x = a
ho cos varphi sin heta , >;; < y = b
ho sin varphi sin heta , >;; < z = c
ho cos heta . >$ Модуль якобиана данного преобразования равен (left| I
ight| = abc <
ho ^2 >sin heta .) Поэтому для дифференциалов справедливо соотношение $dxdydz = abc <
ho ^2 >sin heta d
ho dvarphi d heta .$ В новых координатах интеграл принимает вид: $ < I = iiintlimits_U < left( < frac < < < x^2 >> > < < < a^2 >> > + frac < < < y^2 >> > < < < b^2 >> > + frac < < < z^2 >> > < < < c^2 >> > >
ight)dxdydz > > = < iiintlimits_ < U’ >< left[ < frac < < < < left( < a
ho cos varphi sin heta >
ight) > ^2 > > > < < < a^2 >> > + frac < < < < left( < b
ho sin varphi sin heta >
ight) > ^2 > > > < < < b^2 >> > + frac < < < < left( < c
ho cos heta >
ight) > ^2 > > > < < < c^2 >> > >
ight]abc <
ho ^2 >sin heta d
ho dvarphi d heta > > = \ = < iiintlimits_ < U’ > < left[ < <
ho ^2 > < < cos >^2 > varphi , < < sin >^2 > heta + <
ho ^2 > < sin^2 >varphi , < < sin >^2 > heta + <
ho ^2 > < < cos >^2 > heta >
ight]abc <
ho ^2 >sin heta d
ho dvarphi d heta > > = \ = < iiintlimits_ < U’ > < left[ < <
ho ^2 > < < sin >^2 > heta underbrace < left( < < < cos >^2 > varphi + < sin^2 >varphi >
ight) > _1 + <
ho ^2 > < < cos >^2 > heta >
ight]abc <
ho ^2 >sin heta d
ho dvarphi d heta > > = \ = < iiintlimits_ < U’ > < <
ho ^2 >underbrace < left( < < sin^2 > heta + < < cos >^2 > heta >
ight) > _1abc <
ho ^2 >sin heta d
ho dvarphi d heta > > = < abciiintlimits_ < U’ > < <
ho ^4 >sin heta d
ho dvarphi d heta > . > $
Вычислить интеграл $intlimits_0^1 < dx >intlimits_0^ < sqrt < 1 — < x^2 >> > < dy >intlimits_0^ < sqrt < 1 — < x^2 >- < y^2 >> > < < < left( < < x^2 >+ < y^2 >+ < z^2 >>
ight) > ^2 > dz > ,$ используя сферические координаты.
Решение:
Область интегрирования представляет собой часть шара, расположенная в первом октанте и, следовательно, ограничена неравенствами $ < 0 le
ho le 1, >;; < 0 le varphi le frac < pi > < 2 >, > ;; < 0 le heta le frac < pi > < 2 >. > $
Далее:
Формулы. Равенство функций и эквивалентность формул. Основные эквивалентности
Вычисление криволинейного интеграла первого рода. Примеры
Определение тройного интеграла. Теорема существования тройного интеграла
Выражение площади плоской области через криволинейный интеграл
Частные случаи векторных полей
Скалярное поле, производная по направлению, градиент
Функции k-значной логики. Элементарные функции. Лемма об аналоге правила де Моргана
Вычисление криволинейного интеграла второго рода. Примеры.
Механические и физические приложения поверхностного интеграла первого рода
Вычисление площадей плоских областей
Линейный интеграл и циркуляция векторного поля
Решение задач с помощью алгебры высказываний
Вычисление криволинейного интеграла первого рода. Плоский случай
Поверхностный интеграл первого рода и его свойства
Огравление $Rightarrow $