В основном мы остановимся на свойствах функций, которые имеют широкое применение в экономических исследованиях, в экономической практике анализа и принятия решений.
Путь имеется функция нескольких переменных Y=F(X1, …, хN), где XiXi, YY и область определения будем рассматривать как наборы-векторов (X1, …, хN), на которых функция определена.
Мы уже рассматривали для функции одной переменной определение монотонной функции.
Для функций двух переменных также определяются понятия возрастания или убывания (монотонности) функции.
Определение. Функция Z = f(х, у) называется Возрастающей ( убывающей ) по переменной 

Функция f(X), заданная в выпуклой области, называетсявыпуклой вниз (вверх), если для любых точек Х (1) , Х (2) из области ее определения и любого числа 0 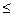
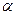
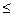
f( 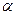
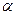
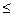
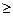
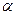
Для функции одной переменной это означает, что выпуклая вверх функция лежит выше отрезка, соединяющего любые две точке ее графика, а выпуклая вниз – ниже.
Определение выпуклой функции уже давалось ранее при изучении исследования функций с помощью дифференциального счисления, только вместо формулы отрезка использовалась формула, определяющая середину отрезка (см. рисунок 3.7).
Если неравенства в определении выполняются, как строгие, то функция называется строго выпуклой. В соответствии с этим определением линейная функция является нестрого выпуклой одновременно вверх и вниз.
Для выпуклой функции равенство нулю частных производных является не только необходимым, но и достаточным условием экстремума. Т.е. если функция является строго выпуклой на всей рассматриваемой области, и получена стационарная точка, то в ней достигается глобальный максимум (при выпуклости вверх) или минимум (при выпуклости вниз).
Для отыскания глобального максимума (наибольшего значения) выпуклой вниз функции или глобального минимума (наименьшего значения) выпуклой вверх функции достаточно исследования экстремумов только на границе области определения.
Условный экстремум
Рассмотренные выше ситуации поиска локальных и глобальных экстремумов представляли собой задачи нахождения безусловных экстремумов, или задачи безусловной оптимизации. Если на аргументы функции наложены некоторые дополнительные ограничениями в форме равенств, то задача оптимизации превращается в задачу на условный экстремум.
Такую задачу можно записать в общем виде следующим образом:
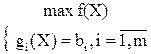

где Х=(х1, х2, . . . хn), а выражения gi(X) = b i называют уравнениями связи, m – число таких уравнений (запись 
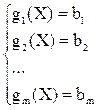
Если есть возможность выразить из ограничений задачи m переменных через (n-m) остальных, то тривиальным подходом к решению является подстановка этих переменных в целевую функцию и далее безусловная оптимизация полученной функции.
Если такой возможности нет, то для нахождения условного экстремума в математическом анализе используют метод множителей Лагранжа. Он состоит в том, что строится функция Лагранжа, имеющая следующий вид:
L(x1, . . ., xn, l1, . . ., lm) = f(x1, . . ., xn) + 
где li, 
Можно доказать, что если задача на условный экстремум имеет решение в некоторой точке, то существуют такие значения множителей Лагранжа, что вместе с координатами этой точки они будут представлять собой точку экстремума функции Лагранжа. Поэтому для решения задачи достаточно провести исследование на экстремум функции Лагранжа.
Не нашли то, что искали? Воспользуйтесь поиском:
Выше мы дали определение выпуклого множества: напомним, что множество — выпуклое, если вместе с любыми двумя точками множеству принадлежат все точки отрезка, соединяющего в пространстве точку с точкой . Заметим, что отрезок, состоящий из точек , можно параметризовать следующим образом: Тогда при будет получаться точка , при — точка , а при — промежуточные точки отрезка, так что обозначения точек отрезка как будут согласованы с обозначениями его концов.
На следующем рисунке изображены два множества на плоскости : одно выпуклое, а другое нет.
Выпуклыми в пространстве являются, например, такие множества: всё пространство , его положительный октант 0, i=1,dots,n>$ —> 0, i=1,dots,n>$" src="http://rstud.ru/end4/images/img3485.png" img3485.png" w > и неотрицательный октант , любой шар, как открытый , так и замкнутый , любая гиперплоскость (заданная некоторым уравнением вида , а также открытое и замкнутое полупространства, заданные, соответственно, условиями 0$ —> 0$" src="http://rstud.ru/end4/images/img3489.png" img3489.png" w > и .
Заметим также, что, согласно определению, выпуклы также все одноточечные множества и пустое множество .
Доказательство . Пусть точки и принадлежат ; тогда обе они принадлежат каждому из множеств . Значит, если — произвольная точка отрезка, соединяющего и , то она принадлежит , поскольку выпукло. Но так как для всех , то , что и требовалось доказать.
Из этой теоремы следует, например, что прямая в -мерном пространстве (её можно задать как векторным уравнением: , где — фиксированные векторы, а — параметр, так и в виде пересечения гиперплоскостей ) является выпуклым множеством. Действительно, каждая гиперплоскость — выпуклое множество.
Проколотая окрестность любой точки , то есть множество ( 0$ —> 0$" src="http://rstud.ru/end4/images/img1353.png" img1353.png" w > ), не является выпуклым. Чтобы показать это, достаточно выбрать любой ненулевой вектор длины меньше и рассмотреть точки проколотой окрестности и , расположенные симметрично относительно точки . Тогда середина отрезка, соединяющего с , то есть точка , совпадает с и, следовательно, не лежит в проколотой окрестности точки .
Если , то есть речь идёт о подмножествах прямой , то выпуклые множества можно описать полностью: это а) пустое множество; б) все одноточечные множества; в) все интервалы вида (где может равняться , а может равняться ); г) все полуинтервалы вида (где может равняться ) и (где может равняться ); наконец, д) все отрезки вида . Никаких других выпуклых множеств на прямой нет.
Напомним изученное в первом семестре определение выпуклой функции одного вещественного переменного.
и вогнутой (или выпуклой кверху ), если выполняется неравенство
(То есть функция вогнута в том и только том случае, если функция выпукла.)
В левой части этого неравенства стоит значение функции в производной точке
отрезка между и (будем для простоты считать, что ), а в правой части неравенства — значение линейной функции , такой что и (см. рис.).
Если и , то неравенство, означающее выпуклость функции , превращается в такое:
Дадим теперь определение выпуклой функции многих переменных.
Функция называется вогнутой (или выпуклой кверху ) в , если функция вогнута.
Таким образом, функция вогнута в том и только том случае, когда функция выпукла.
Выпуклость функции в означает, что для любого отрезка с концами и параметризация этого отрезка в виде задаёт композицию , являющуюся выпуклой функцией параметра . Ввиду выпуклости области , любые точки и отрезка лежат в , и их снова можно взять в качестве концов отрезка. Поэтому для выпуклости функции в области необходимо и достаточно, чтобы неравенство
выполнялось при всех и .
Если при этом при всех и выполняется строгое неравенство
то функцию будем называть строго выпуклой в .
Наконец, функция называется строго вогнутой , если функция строго выпукла; это означает выполнение строгого неравенства
Геометрически (в случае ) строгая выпуклость означает, что для любой хорды графика точки дуги графика с теми же концами, что у хорды, лежащие в вертикальном сечении, проходящем через эту хорду, располагаются ниже точек хорды. Строгая вогутость означает, что в любом вертикальном сечении график проходит выше любого отрезка, соединяющего две точки графика.
Заметим, что понятия выпуклой и вогнутой функций (а также строго выпуклой и строго вогнутой функций) в области определены только для выпуклых областей .
Дадим теперь такое алгебраическое определение.
Заметим, что выражение можно записать в виде , где — это матрица-строка, равная транспонированному столбцу . Вообще, верхний левый индекс мы будем применять для обозначения транспонированной матрицы.
У симметричной матрицы равны друг другу элементы, расположенные симметрично друг другу относительно главной диагонали матрицы.
является выпуклой функцией (во всем пространстве, то есть при ).
Если же симметричная матрица — положительно определённая, то заданная ею квадратичная форма является строго выпуклой.
Доказательство . Пусть и — две произвольные точки и , где , — точка отрезка, соединяющего с .
Предположим, что матрица неотрицательно определена. Элементарные преобразования позволяют записать в виде
Поскольку матрица неотрицательно определена, имеет место неравенство
откуда сразу следует, что
а это неравенство означает выпуклость функции .
Доказательство строгой выпуклости в случае положительно определённой матрицы проводится с помощью очевидных изменений приведённого доказательства.
Другой пример выпуклой функции даёт линейная функция:
где — постоянные, является выпуклой функцией во всём пространстве (но не является строго выпуклой функцией). Действительно, как легко проверить, при всех и имеем
Поскольку функция , очевидно, также линейна, линейная функция является одновременно и вогнутой (но не строго вогнутой).
Если о некоторых функциях известно, что они выпуклы в области , то из них можно сконструировать другие выпуклые функции, используя следующие свойства выпуклых функций.
Доказательство . Пусть и , где . Тогда
что и означает выпуклость функции .
Поскольку, как мы доказали выше, квадратичная функция с неотрицательно определённой матрицей и линейная функция выпуклы, то и их сумма, согласно доказанному свойству, — выпуклая функция. В качестве упражнения докажите, однако, ещё одно утверждение, не вытекающее из теоремы 7.17:
Указание: по сути дела, нужно повторить доказательство теоремы 7.16, с очевидными изменениями.
Доказательство . Пусть снова и , где . Тогда
что и означает выпуклость функции . Первое неравенство в (7.11*) следует из того, что функция выпукла, а второе — из того, что при всех имеет место неравенство:
а при всех — равенство
(Проверьте, что последние два утверждения действительно верны.)
Доказательство . Пусть снова и , где . Тогда, ввиду того что , получаем:
Последнее неравенство следует из того, что при .
Следующие три утверждения остаются читателю для самостоятельного доказательства в качестве упражнения.
Если функции и выпуклы в области , то функция также выпукла в .
Если функция выпукла в области , а функция одного переменного выпукла на интервале , содержащем множество значений функции при всех , и возрастает всюду на интервале или убывает всюду на , то композиция выпукла в . (Например, если функция выпукла в , то функция также будет выпуклой в .)
Выпуклые функции интересны такой своей особенностью: они не могут иметь нескольких локальных минимумов с разными значениями.
Сначала дадим такое определение.
Точка называется точкой локального минимума функции , если существует такая окрестность , 0$ —> 0$" src="http://rstud.ru/end4/images/img1353.png" img1353.png" w > , что при всех . Если при этом f(x^0)$ —> f(x^0)$" src="http://rstud.ru/end4/images/img3584.png" img3584.png" w > при всех , не совпадающих с , то точка называется точкой строгого локального минимума . И в том и в другом случае значение называется локальным минимумом функции .
Точка называется точкой локального максимума функции , если существует такая окрестность , 0$ —> 0$" src="http://rstud.ru/end4/images/img1353.png" img1353.png" w > , что при всех . Если при этом при всех , не совпадающих с , то точка называется точкой строгого локального максимума . И в том и в другом случае значение называется локальным максимумом функции .
Доказательство . Очевидно, что достаточно доказать лишь первое утверждение: второе следует из него сменой знака функции.
Пусть — точка локального минимума, а в некоторой другой точке функция имеет меньшее значение: . Тогда в точках отрезка, соединяющего с , то есть точках , при всех 0$ —> 0$" src="http://rstud.ru/end4/images/img3588.png" img3588.png" w > значения функции будут меньше, чем в точке :
Но точки с 0$ —> 0$" src="http://rstud.ru/end4/images/img3588.png" img3588.png" w > имеются в любой, сколь угодно малой, окрестности точки , что противоречит предположению о том, что — точка локального минимума. Значит, неравенство невозможно, и для любой точки . Это означает, что значение функции в точке локального минимума — наименьшее во всей области .
Практическая ценность этого утверждения в том, что при поиске наименьшего значения выпуклой функции в области достаточно найти любую точку локального минимума; во всех остальных точках локального минимуцма (если они существуют) значение функции будет точно такое же. Для невыпуклых функций это, конечно, не так, как видно на следующем рисунке:
Имеет место также следующая
Доказательство . Пусть в двух разных точках и функция принимает одно и то же значение Поскольку функция строго выпукла, то в точках , не совпадающих с и с , должно выполняться неравенство
Но это означает, что в точках , например, в середине отрезка , значение меньше , что противоречит предположению о том, что значение — наименьшее во всей области. Значит, второй точки с тем же минимальным значением нет.
Эти требования требуется выполнять при оформлении контрольных работ по предмету математика. Кроме того при выполнении самой контрольной работы по предмету математика не обязательно решать задачи в строгом порядке с их нумерацией. Приступив к решению задачи, и не найдя сразу пути решения этой задачи, лучший выход — отложить ее в сторону, и приступить к решению задачи которая сейчас для вас более понятна.


