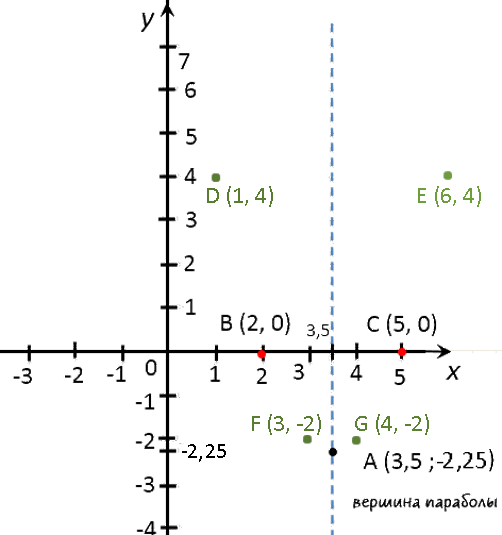Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют функцией в математике.
Если вы прочно закрепите общие знания о функции (способы задания, понятие графика) дальнейшее изучение других видов функций будет даваться значительно легче.
Что называют квадратичной функцией
Квадратичная функция — это функция вида
Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень, в которой стоит « x » — это « 2 », то перед нами квадратичная функция.
Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты « a », « b » и « с ».
| Квадратичная функция | Коэффициенты |
|---|---|
| y = 2x 2 − 7x + 9 |
|
| y = 3x 2 − 1 |
|
| y = −3x 2 + 2x |
|
Как построить график квадратичной функции
График квадратичной функции называют параболой.
Парабола выглядит следующим образом.
Также парабола может быть перевернутой.
Существует четкий алгоритм действий при построении графика квадратичной функции. Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.
Чтобы было проще понять этот алгоритм, сразу разберем его на примере.
Построим график квадратичной функции « y = x 2 −7x + 10 ».
- Направление ветвей параболы
Если « a > 0 », то ветви направлены вверх.
Если « a », то ветви направлены вниз.
В нашей функции « a = 1 », это означает, что ветви параболы направлены вверх.
Координаты вершины параболы
Чтобы найти « x0 » (координата вершины по оси « Ox ») нужно использовать формулу:
x0 =
| −b |
| 2a |
Найдем « x0 » для нашей функции « y = x 2 −7x + 10 ».
x0 =
| − (−7) |
| 2 · 1 |
=
| 7 |
| 2 |
= 3,5
Теперь нам нужно найти « y0 » (координату вершины по оси « Oy »). Для этого нужно подставить найденное значение « x0 » в исходную функцию. Вспомнить, как найти значение функции можно в уроке «Как решать задачи на функцию» в подразделе «Как получить значение функции».
Выпишем полученные координаты вершины параболы.
(·) A (3,5; −2,25) — вершина параболы.
Отметим вершину параболы на системе координат. Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график относительно оси « Oy ».
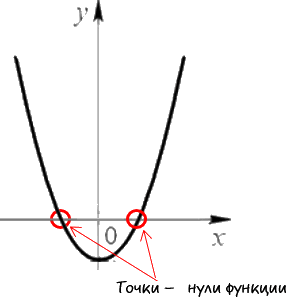
Для начала давайте разберемся, что называют нулями функции.
Нули функции — это точки пересечения графика функции с осью « Ox » (осью абсцисс).
Наглядно нули функции на графике выглядят так:
Свое название нули функции получили из-за того, что у этих точек координата по оси « Oy » равна нулю.
Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.
Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо « y = 0 ».
Подставим в заданную функцию « y = x 2 −7x + 10 » вместо « y = 0 » и решим полученное квадратное уравнение относительно « x » .
0 = x 2 −7x + 10
x 2 −7x + 10 = 0
x1;2 =
| 7 ± √ 49 − 4 · 1 · 10 |
| 2 · 1 |
x1;2 =
| 7 ± √ 9 |
| 2 |
x1;2 =
| 7 ± 3 |
| 2 |
| x1 = |
| 7 + 3 |
| 2 |
Мы получили два корня в уравнении, значит, у нас две точки пересечения с осью « Ox ». Назовем эти точки и выпишем их координаты.
Отметим полученные точки («нули функции») на системе координат.
Возьмем четыре произвольные числовые значения для « x ». Целесообразно брать целые числовые значения на оси « Ox », которые наиболее близки к оси симметрии. Числа запишем в таблицу в порядке возрастания.
| x | 1 | 3 | 4 | 6 |
| y |
Для каждого выбранного значения « x » рассчитаем « y ».
- y(1) = 1 2 − 7 · 1 + 10 = 1 − 7 + 10 = 4
- y(3) = 3 2 − 7 · 3 + 10 = 9 − 21 + 10 = −2
- y(4) = 4 2 − 7 · 4 + 10 = 16 − 28 + 10 = −2
- y(6) = 6 2 − 7 · 6 + 10 = 36 − 42 + 10 = 4
Запишем полученные результаты в таблицу.
| x | 1 | 3 | 4 | 6 |
| y | 4 | −2 | −2 | 4 |
Отметим полученные точки графика на системе координат (зеленые точки).
Теперь мы готовы построить график. На забудьте после построения подписать график функции.
Краткий пример построения параболы
Рассмотрим другой пример построения графика квадратичной функции. Только теперь запишем алгоритм построения коротко без подробностей.
Пусть требуется построить график функции « y = −3x 2 − 6x − 4 ».
- Направление ветвей параболы « a = −3 » — ветви параболы направлены вниз.

Координаты вершины параболы
x0 =
| −b |
| 2a |
x0 =
| −(−6) |
| 2 · (−3) |
=
| 6 |
| −6 |
= −1
y0(−1) = (−3) · (−1) 2 − 6 · (−1) − 4 = −3 · 1 + 6 − 4 = −1
(·) A (−1; −1) — вершина параболы.
Точки пересечения с осью « Ox » ( y = 0 ).
−3x 2 − 6x − 4 = 0 |·(−1)
x1;2 =
| −6 ± √ 6 2 − 4 · 3 · 4 |
| 2 · 1 |
x1;2 =
| −6 ± √ 36 − 48 |
| 2 |
x1;2 =
| −6 ± √ −12 |
| 2 |
Ответ: нет действительных корней.
Так как корней нет, значит, график функции не пересекает ось « Ox ».
Вспомогательные точки для: « x = −3 »; « x = −2 »; « x = 0 »; « x = 1 ». Подставим в исходную функцию « y = −3x 2 − 6x − 4 ».
- y(−3) = −3 · (−3) 2 − 6 · (−3) − 4 = −3 · 9 + 18 − 4 = −27 + 14 = −13
- y(−2) = −3 · (−2) 2 − 6 · (−2) − 4 = −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4
- y(0) = −3 · 0 2 − 6 · 0 − 4 = −4
- y(1) = −3 · 1 2 − 6 · 1 − 4 = −3 −6 − 4 = −13
| x | −3 | −2 | 0 | 1 |
| y | −13 | −4 | −4 | −13 |
Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые не выходят за масштаб нашей системы координат, то есть точки « (−2; −4) » и « (0; −4) ». Построим и подпишем график функции.
Урок: как построить параболу или квадратичную функцию?
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Парабола — это график функции описанный формулой ax 2 +bx+c=0.
Чтобы построить параболу нужно следовать простому алгоритму действий:
1 ) Формула параболы y=ax 2 +bx+c,
если а>0 то ветви параболы направленны вверх,
а 2 +bx+c=0;
a) Полное квадратное уравнение имеет вид ax 2 +bx+c=0 и решается по дискриминанту;
b) Неполное квадратное уравнение вида ax 2 +bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0:
ax 2 +bx=0,
х(ax+b)=0,
х=0 и ax+b=0;
c)Неполное квадратное уравнение вида ax 2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a);
4) Найти несколько дополнительных точек для построения функции.
ПРАКТИЧЕСКАЯ ЧАСТЬ
И так теперь на примере разберем все по действиям:
Пример №1:
y=x 2 +4x+3
c=3 значит парабола пересекает OY в точке х=0 у=3. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2) 2 +4*(-2)+3=4-8+3=-1 вершина находится в точке (-2;-1)
Найдем корни уравнения x 2 +4x+3=0
По дискриминанту находим корни
a=1 b=4 c=3
D=b 2 -4ac=16-12=4
x=(-b±√(D))/2a
x1=(-4+2)/2=-1
x2=(-4-2)/2=-3 
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=-2
х -4 -3 -1 0
у 3 0 0 3
Подставляем вместо х в уравнение y=x 2 +4x+3 значения
y=(-4) 2 +4*(-4)+3=16-16+3=3
y=(-3) 2 +4*(-3)+3=9-12+3=0
y=(-1) 2 +4*(-1)+3=1-4+3=0
y=(0) 2 +4*(0)+3=0-0+3=3
Видно по значениям функции,что парабола симметрична относительно прямой х=-2
Пример №2:
y=-x 2 +4x
c=0 значит парабола пересекает OY в точке х=0 у=0. Ветви параболы смотрят вниз так как а=-1 -1 2 +4*2=-4+8=4 вершина находится в точке (2;4)
Найдем корни уравнения -x 2 +4x=0
Неполное квадратное уравнение вида ax 2 +bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0.
х(-x+4)=0, х=0 и x=4. 
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=2
х 0 1 3 4
у 0 3 3 0
Подставляем вместо х в уравнение y=-x 2 +4x значения
y=0 2 +4*0=0
y=-(1) 2 +4*1=-1+4=3
y=-(3) 2 +4*3=-9+13=3
y=-(4) 2 +4*4=-16+16=0
Видно по значениям функции,что парабола симметрична относительно прямой х=2
Пример №3
y=x 2 -4
c=4 значит парабола пересекает OY в точке х=0 у=4. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0) 2 -4=-4 вершина находится в точке (0;-4)
Найдем корни уравнения x 2 -4=0
Неполное квадратное уравнение вида ax 2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
x 2 =4
x1=2
x2=-2
Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=0
х -2 -1 1 2
у 0 -3 -3 0
Подставляем вместо х в уравнение y= x 2 -4 значения
y=(-2) 2 -4=4-4=0
y=(-1) 2 -4=1-4=-3
y=1 2 -4=1-4=-3
y=2 2 -4=4-4=0
Видно по значениям функции,что парабола симметрична относительно прямой х=0
Подписывайтесь на канал на YOUTUBE, чтобы быть в курсе всех новинок и готовится с нами к экзаменам.
Идёт приём заявок
Подать заявку
Для учеников 1-11 классов и дошкольников


Государственное бюджетное общеобразовательное учреждение
средняя школа №1 им. Г. М. Шубникова
Открытый урок в 9 а классе
Построение графика квадратичной функции
Учитель Добрина Л.А.
Тема: «Построение графика квадратичной функции»
— знать определение квадратичной функции, алгоритм построения графика квадратичной функции;
— уметь находить координаты вершины параболы, дополнительные точки, строить параболу;
— воспитывать внимательность, самостоятельность, навыки работы с чертежными принадлежностями, культуру чертежа.
Оборудование: мультимедийный проектор, индивидуальные карточки.
I . Организационный момент.
На прошлом уроке мы изучили алгоритм построения графика квадратичной функции. Сегодня мы продолжим решать задания по этой теме. Какова же цель нашего урока? (повторить определение квадратичной функции, алгоритм построения параболы, продолжить выработку навыков по построению параболы).
II . Проверка домашнего задания. (№105 б,в). Устно назвать свойства функций.
III . Устная работа ( Фронтальный опрос. Одновременно несколько учащихся работают по индивидуальным карточкам: определить направление ветвей параболы и найти координаты вершины параболы). А теперь, прежде, чем перейти к письменной работе, ответьте на вопросы:
1. Функция какого вида называется квадратичной?
2. Что является графиком квадратичной функции? Сколько точек необходимо для построения параболы?
3. От чего зависит направление ветвей параболы?
4. Что называется осью симметрии параболы?
5. Дайте название функции и скажите, что является графиком этой функцц:
у = 2х -5 , у = 8 + 6х, у = 2х 2 – 5, у = 
у = — 
6. Определите, график какой функции изображен на рисунке
А. у = — (х-3) 2 + 1 Б. у = (х+3) 2 -1 В. у = (х-1) 2 +3
Назовите промежутки возрастания и убывания функции.
IV А теперь перейдем к письменной работе.
Задание 1. Постройте график функции у = 

Координаты вершины параболы можно определить по уравнению функции В(0; -2). Найдем дополнительные точки
Задание 2. Постройте график функции у = -х 2 –4х + 3 (выполняет учащийся на доске с комментированием). Квадратичная функция. Графиком является парабола, ветви направлены вниз (а=-1 D (у): R .
Найдем координаты вершины параболы В(х0,у0)
х0 = — 
Найдем дополнительные точки
А теперь физминутка.
1. Повороты головы вправо- влево, вверх- вниз, показываем смещение вершины параболы
у = -х 2 + 3 у = -(х – 2) 2 у = -х 2 + 6
у = = х 2 — 5 у = (х + 1) 2 у = -х 2 – 8
2. Движения руками вверх- вниз, показываем направление ветвей параболы.
у = -х 2 + 3 у = -(х – 2) 2 + 2 у = -х 2 + 6
у = = х 2 — 5 у = (х + 1) 2 — 5 у = -х 2 – 8
Задание 3. График функции у = ах 2 + b х + с проходит через точку А(-1;10) и имеет вершину в точке В(1;-2). Напишите уравнение параболы.
-а – b +с =10, -2 b = 12, b = -6, b = -6, b = -6,
а + b + с = -2, а + b + с = -2, а + b + с = -2, а + b + с = -2, с = 1,
— 

Уравнение параболы у = 3х 2 – 6х + 1
Одним из заданий домашней работы будет построение графика этой параболы.
V А теперь выполните самостоятельно задание
Вариант 1 Вариант 2
Построить график функции:
у = х 2 + 2х — 3 у = х 2 — 2х — 3
VI А теперь подведем итог. На уроке мы должны были алгоритм построения параболы- графика квадратичной функции, закрепить навыки построения параболы, повторить правила определения направления ветвей параболы и координат вершины параболы. Ответьте на следующие вопросы. Верно ли, что:
Графиком функции у=3х+2 является парабола. (Неверно)
(0;0)- координаты вершины параболы у = х 2 — 2 (Неверно)
Прямая х= 0- ось симметрии параболы у = 0,5х 2 . (Верно)
Первый коэффициент функции у=х 2 +4 равен 1, второй — 0, свободный член — 4. (Верно)
Функция у=3х 2 возрастает на множестве всех действительных чисел. (Неверно)
Ветви параболы у= -2х 2 +х+3 направлены вниз. (Верно)
У функции у=5х 2 -х-4 есть наибольшее значение, но нет наименьшего. (Неверно)
Точка В(2;-200) принадлежит графику функции у=-50х 2 . (Верно)
Квадратичная функция задается формулой вида у=ах 2 +вх+с, где а, в, с – любые числа. (Неверно)
График функции у=(х-1) 2 +2 расположен в 3-й и 4-й координатных четвертях. (Неверно)
Функция у = х 2 является возрастающей на промежутке х > 0. ( Верно)
Значения х, при которых квадратичная функция равна нулю, называют … функции.
Точку пересечения параболы с осью симметрии называют … параболы.
При а >0 ветви параболы у = ах2 направлены … .
VII Домашнее задание:№107 ( построить графики и записать свойства функций)
Спасибо за урок.
- Добрина Лариса АнатольевнаНаписать 1063 22.11.2015
Номер материала: ДВ-178100
- 22.11.2015 551
- 22.11.2015 376
- 22.11.2015 448
- 22.11.2015 378
- 22.11.2015 962
- 22.11.2015 505
- 22.11.2015 953
Не нашли то что искали?
Вам будут интересны эти курсы:
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.