Механическая система, которая состоит из материальной точки (тела), висящей на нерастяжимой невесомой нити (ее масса ничтожно мала по сравнению с весом тела) в однородном поле тяжести, называется математическим маятником (другое название – осциллятор). Бывают и другие виды этого устройства. Вместо нити может быть использован невесомый стержень. Математический маятник может наглядно раскрыть суть многих интересных явлений. При малой амплитуде колебания его движение называется гармоническим.
Общие сведения о механической системе
Если маятник находится в положении равновесия (висит отвесно), то сила тяжести будет уравновешиваться силой натяжения нити. Плоский маятник на нерастяжимой нити является системой с двумя степенями свободы со связью. При смене всего одного компонента меняются характеристики всех ее частей. Так, если нитку заменить на стержень, то у данной механической системы будет всего 1 степень свободы. Какими же свойствами обладает математический маятник? В этой простейшей системе под воздействием периодического возмущения возникает хаос. В том случае, когда точка подвеса не двигается, а совершает колебания, у маятника появляется новое положение равновесия. При быстрых колебаниях вверх-вниз эта механическая система приобретает устойчивое положение «вверх тормашками». У нее есть и свое название. Ее называют маятником Капицы.
Свойства маятника
• Если, сохраняя одинаковую длину маятника, подвешивать различные грузы, то период их колебаний получится одинаковым, хотя их массы будут сильно различаться. Следовательно, период такого маятника не зависит от массы груза.
• Если при запуске системы отклонять маятник на не слишком большие, но разные углы, то он станет колебаться с одинаковым периодом, но по разным амплитудам. Пока отклонения от центра равновесия не слишком велики, колебания по своей форме будут достаточно близки гармоническим. Период такого маятника никак не зависит от колебательной амплитуды. Это свойство данной механической системы называется изохронизмом (в переводе с греческого «хронос» — время, «изос» — равный).
Период математического маятника
Этот показатель представляет собой период собственных колебаний. Несмотря на сложную формулировку, сам процесс очень прост. Если длина нити математического маятника L, а ускорение свободного падения g, то эта величина равна:
Период малых собственных колебаний ни в какой мере не зависит от массы маятника и амплитуды колебаний. В этом случае маятник двигается как математический с приведенной длиной.
Колебания математического маятника
Математический маятник совершает колебания, которые можно описать простым дифференциальным уравнением:
где х (t) – неизвестная функция (это угол отклонения от нижнего положения равновесия в момент t, выраженный в радианах); ω – положительная константа, которая определяется из параметров маятника (ω = √g/L, где g – это ускорение свободного падения, а L – длина математического маятника (подвес).
Уравнение малых колебаний вблизи положення равновесия (гармоническое уравнение) выглядит так:
Колебательные движения маятника
Математический маятник, который совершает малые колебания, двигается по синусоиде. Дифференциальное уравнение второго порядка отвечает всем требованиям и параметрам такого движения. Для определения траектории необходимо задать скорость и координату, из которых потом определяются независимые константы:
где θ0 – начальная фаза, A – амплитуда колебания, ω – циклическая частота, определяемая из уравнения движения.
Математический маятник (формулы для больших амплитуд)
Данная механическая система, совершающая свои колебания со значительной амплитудой, подчиняется более сложным законам движения. Для такого маятника они рассчитываются по формуле:
sin x/2 = u * sn(ωt/u),
где sn — синус Якоби, который для u 2 августа, 2014
Сохранение энергии при колебаниях математического маятника
При гармонических колебаниях полная механическая энергия системы сохраняется (остается постоянной).
Полная механическая энергия математического маятника складывается из кинетической энергии и потенциальной энергии:
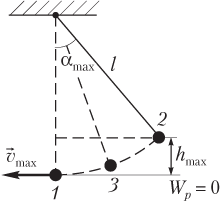
где W k — кинетическая энергия, W k = = mv 2 /2; W p — потенциальная энергия, W p = mgh ; m — масса груза; g — модуль ускорения свободного падения; v — модуль скорости груза; h — высота подъема груза над положением равновесия (рис. 10.15).
В Международной системе единиц энергия механической колебательной системы измеряется в джоулях (1 Дж).
При гармонических колебаниях математический маятник проходит ряд последовательных состояний, поэтому целесообразно рассмотреть энергию математического маятника в трех положениях (см. рис. 10.15):
1) в положении равновесия ( 1 ) скорость тела имеет максимальное значение v max , поэтому кинетическая энергия также максимальна:
W k max = m v max 2 2 ;
потенциальная энергия равна нулю; полная энергия совпадает с максимальной кинетической энергией:
2) в крайнем положении ( 2 ) тело поднято над исходным уровнем на максимальную высоту h max , поэтому потенциальная энергия также максимальна:
W p max = m g h max ;
кинетическая энергия равна нулю; полная энергия совпадает с максимальной потенциальной энергией:
3) в промежуточном положении ( 3 ) тело обладает мгновенной скоростью v и поднято над исходным уровнем на некоторую высоту h , поэтому полная энергия представляет собой сумму
E = m v 2 2 + m g h ,
где mv 2 /2 — кинетическая энергия; mgh — потенциальная энергия; m — масса груза; g — модуль ускорения свободного падения; v — модуль скорости груза; h — высота подъема груза над положением равновесия.
При гармонических колебаниях математического маятника полная механическая энергия сохраняется:
Значения полной энергии математического маятника в трех его положениях отражены в табл. 10.1.
| № | Положение | W p | W k | E = W p + W k |
|---|---|---|---|---|
| 1 | Равновесие | 0 | m v max 2 / 2 | m v max 2 / 2 |
| 2 | Крайнее | mgh max | 0 | mgh max |
| 3 | Промежуточное (мгновенное) | mgh | mv 2 /2 | mv 2 /2 + mgh |
Значения полной механической энергии, представленные в последнем столбце табл. 10.1, имеют равные значения для любых положений маятника, что является математическим выражением закона сохранения полной механической энергии :
m v max 2 2 = m g h max ;
m v max 2 2 = m v 2 2 + m g h ;
m g h max = m v 2 2 + m g h ,
где m — масса груза; g — модуль ускорения свободного падения; v — модуль мгновенной скорости груза в положении 3 ; h — высота подъема груза над положением равновесия в положении 3 ; v max — модуль максимальной скорости груза в положении 1 ; h max — максимальная высота подъема груза над положением равновесия в положении 2 .
Угол отклонения нити математического маятника от вертикали (рис. 10.15) определяется выражением
cos α = l − h l = 1 − h l ,
где l — длина нити; h — высота подъема груза над положением равновесия.
Максимальный угол отклонения α max определяется максимальной высотой подъема груза над положением равновесия h max :
cos α max = 1 − h max l .
Пример 11. Период малых колебаний математического маятника равен 0,9 с. На какой максимальный угол от вертикали будет отклоняться нить, если, проходя положение равновесия, шарик движется со скоростью, равной 1,5 м/с? Трение в системе отсутствует.
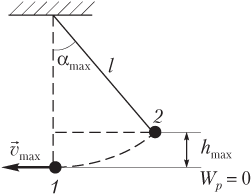
Решение . На рисунке показаны два положения математического маятника:
- положение равновесия 1 (характеризуется максимальной скоростью шарика v max );
- крайнее положение 2 (характеризуется максимальной высотой подъема шарика h max над положением равновесия).
Искомый угол определяется равенством
cos α max = l − h max l = 1 − h max l ,
где l — длина нити маятника.
Максимальную высоту подъема шарика маятника над положением равновесия найдем из закона сохранения полной механической энергии.
Полная энергия маятника в положении равновесия и в крайнем положении определяется следующими формулами:
E 1 = m v max 2 2 ,
где m — масса шарика маятника; v max — модуль скорости шарика в положении равновесия (максимальная скорость), v max = 1,5 м/с;
где g — модуль ускорения свободного падения; h max — максимальная высота подъема шарика над положением равновесия.
Закон сохранения полной механической энергии:
m v max 2 2 = m g h max .
Выразим отсюда максимальную высоту подъема шарика над положением равновесия:
h max = v max 2 2 g .
Длину нити определим из формулы для периода колебаний математического маятника
Подставим h max и l в выражение для косинуса искомого угла:
cos α max = 1 − 2 π 2 v max 2 g 2 T 2
и произведем вычисление с учетом приблизительного равенства π 2 = 10:
cos α max = 1 − 2 ⋅ 10 ⋅ ( 1,5 ) 2 10 2 ⋅ ( 0,9 ) 2 = 0,5 .
Отсюда следует, что максимальный угол отклонения составляет 60°.
Строго говоря, при угле 60° колебания шарика не являются малыми и пользоваться стандартной формулой для периода колебаний математического маятника неправомерно.
Сохранение энергии при колебаниях пружинного маятника
Полная механическая энергия пружинного маятника складывается из кинетической энергии и потенциальной энергии:
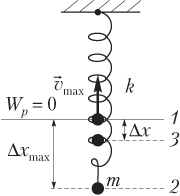
где W k — кинетическая энергия, W k = mv 2 /2; W p — потенциальная энергия, W p = k (Δ x ) 2 /2; m — масса груза; v — модуль скорости груза; k — коэффициент жесткости (упругости) пружины; Δ x — деформация (растяжение или сжатие) пружины (рис. 10.16).
В Международной системе единиц энергия механической колебательной системы измеряется в джоулях (1 Дж).
При гармонических колебаниях пружинный маятник проходит ряд последовательных состояний, поэтому целесообразно рассмотреть энергию пружинного маятника в трех положениях (см. рис. 10.16):
1) в положении равновесия ( 1 ) скорость тела имеет максимальное значение v max , поэтому кинетическая энергия также максимальна:
W k max = m v max 2 2 ;
потенциальная энергия пружины равна нулю, так как пружина не деформирована; полная энергия совпадает с максимальной кинетической энергией:
2) в крайнем положении ( 2 ) пружина имеет максимальную деформацию (Δ x max ), поэтому потенциальная энергия также имеет максимальное значение:
W p max = k ( Δ x max ) 2 2 ;
кинетическая энергия тела равна нулю; полная энергия совпадает с максимальной потенциальной энергией:
3) в промежуточном положении ( 3 ) тело обладает мгновенной скоростью v , пружина имеет в этот момент некоторую деформацию (Δ x ), поэтому полная энергия представляет собой сумму
E = m v 2 2 + k ( Δ x ) 2 2 ,
где mv 2 /2 — кинетическая энергия; k (Δ x ) 2 /2 — потенциальная энергия; m — масса груза; v — модуль скорости груза; k — коэффициент жесткости (упругости) пружины; Δ x — деформация (растяжение или сжатие) пружины.
При смещении груза пружинного маятника от положения равновесия на него действует возвращающая сила , проекция которой на направление движения маятника определяется формулой
где x — смещение груза пружинного маятника от положения равновесия, x = ∆ x , ∆ x — деформация пружины; k — коэффициент жесткости (упругости) пружины маятника.
При гармонических колебаниях пружинного маятника полная механическая энергия сохраняется:
Значения полной энергии пружинного маятника в трех его положениях отражены в табл. 10.2.
| № | Положение | W p | W k | E = W p + W k |
|---|---|---|---|---|
| 1 | Равновесие | 0 | m v max 2 / 2 | m v max 2 / 2 |
| 2 | Крайнее | k (Δ x max ) 2 /2 | 0 | k (Δ x max ) 2 /2 |
| 3 | Промежуточное (мгновенное) | k (Δ x ) 2 /2 | mv 2 /2 | mv 2 /2 + k (Δ x ) 2 /2 |
Значения полной механической энергии, представленные в последнем столбце таблицы, имеют равные значения для любых положений маятника, что является математическим выражением закона сохранения полной механической энергии :
m v max 2 2 = k ( Δ x max ) 2 2 ;
m v max 2 2 = m v 2 2 + k ( Δ x ) 2 2 ;
k ( Δ x max ) 2 2 = m v 2 2 + k ( Δ x ) 2 2 ,
где m — масса груза; v — модуль мгновенной скорости груза в положении 3 ; Δ x — деформация (растяжение или сжатие) пружины в положении 3 ; v max — модуль максимальной скорости груза в положении 1 ; Δ x max — максимальная деформация (растяжение или сжатие) пружины в положении 2 .
Пример 12. Пружинный маятник совершает гармонические колебания. Во сколько раз его кинетическая энергия больше потенциальной в тот момент, когда смещение тела из положения равновесия составляет четверть амплитуды?
Решение . Сравним два положения пружинного маятника:
- крайнее положение 1 (характеризуется максимальным смещением груза маятника от положения равновесия x max );
- промежуточное положение 2 (характеризуется промежуточными значениями смещения от положения равновесия x и скорости v → ).
Полная энергия маятника в крайнем и промежуточном положениях определяется следующими формулами:
E 1 = k ( Δ x max ) 2 2 ,
где k — коэффициент жесткости (упругости) пружины; ∆ x max — амплитуда колебаний (максимальное смещение от положения равновесия), ∆ x max = A ;
- в промежуточном положении —
E 2 = k ( Δ x ) 2 2 + m v 2 2 ,
где m — масса груза маятника; ∆ x — смещение груза от положения равновесия, ∆ x = A /4.
Закон сохранения полной механической энергии для пружинного маятника имеет следующий вид:
k ( Δ x max ) 2 2 = k ( Δ x ) 2 2 + m v 2 2 .
Разделим обе части записанного равенства на k (∆ x ) 2 /2:
( Δ x max Δ x ) 2 = 1 + m v 2 2 ⋅ 2 k Δ x 2 = 1 + W k W p ,
где W k — кинетическая энергия маятника в промежуточном положении, W k = mv 2 /2; W p — потенциальная энергия маятника в промежуточном положении, W p = k (∆ x ) 2 /2.
Выразим из уравнения искомое отношение энергий:
W k W p = ( Δ x max Δ x ) 2 − 1
и рассчитаем его значение:
W k W p = ( A A / 4 ) 2 − 1 = 16 − 1 = 15 .
В указанный момент времени отношение кинетической и потенциальной энергий маятника равно 15.
07.06.2019
5 июня Что порешать по физике
30 мая Решения вчерашних ЕГЭ по математике
Математический маятник, колеблющийся с циклической частотой ω = 3 с −1 , в нижней точке траектории имеет ускорение, равное по модулю a = 1 м/с 2 . Масса груза маятника m = 900 г. Чему равен запас механической энергии маятника?
Циклическая частота колебаний математического маятника равна где
— длина маятника. Выражаем
В нижней точке траектории тангенциальная составляющая ускорения отсутствует, ускорение является центростремительным, оно равно
Получаем
В нижней точке траектории механическая энергия маятника равна его кинетической энергии. В итоге получаем: