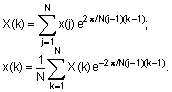Быстрое преобразование фурье матлаб

Дискретные прямое и обратное преобразования Фурье для одномерного массива x длины N определяются следующим образом:

Функция Y = fft(X) вычисляет для массива данных X дискретное преобразование Фурье, используя FFT-алгоритм быстрого Фурье-преобразования. Если массив X двумерный, вычисляется дискретное преобразование каждого столбца.

Функция Y = fft(X, n) вычисляет n-точечное дискретное преобразование Фурье. Если length(X) n, то лишние строки удаляются.

Функция X = ifft(Y) вычисляет обратное преобразование Фурье для массива Y.

Функция X = ifft(Y, n) вычисляет n-точечное обратное преобразование Фурье для массива Y.

Примеры:

Основное назначение преобразования Фурье — выделить частоты регулярных составляющих сигнала, зашумленного помехами. Рассмотрим данные, поступающие с частотой 1000 Гц. Сформируем сигнал, содержащий регулярные составляющие с частотами 50 Гц и 120 Гц и случайную аддитивную компоненту с нулевым средним.

t = 0:0.001:0.6;
x = sin(2 * pi * 50 * t) + sin(2 * pi * 120 * t);
y = x + 2 * randn(size(t));
plot(y(1:50)), grid

На рис. а показан этот сигнал. Глядя на него, трудно сказать, каковы частоты его регулярных составляющих. Реализуя одномерное преобразование Фурье этого сигнала на основе 512 точек и построив график спектральной плотности (рис. б), можно выделить две частоты, на которых амплитуда спектра максимальна. Это частоты 120 и 50 Гц.

Y = fft(y, 512);
Pyy = Y.*conj(Y)/512;
f = 1000 * (0:255)/512;
figure(2), plot(f, Pyy(1:256)), grid


а)	б)

Если длина последовательности входных данных является степенью числа 2, то применяется алгоритм быстрого преобразования Фурье с основанием 2, имеющий максимальную производительность. Этот алгоритм оптимизирован для работы с действительными данными; если данные комплексные, то реализуется комплексное преобразование Фурье. Эффективность первого на 40 % выше второго.

Если длина входной последовательности не является степенью числа 2, то применяется преобразование со смешанными основаниями, которые определяются как простые множители длины входной последовательности, которая при необходимости подвергается усечению.

Время расчета существенно зависит от значения длины последовательности. Если значение длины точно разлагается на простые множители, то вычисления для такой последовательности выполняются достаточно быстро; если же не все множители оказываются простыми, и даже их будет меньше, то время вычисления существенно возрастает.

Если сравнивать эффективность вычислений, то преобразование Фурье с основанием 2 действительной последовательности из 4096 точек занимает 2.1 с, а комплексной — 3.7 с. Обычное преобразование Фурье для последовательности из 4096 точек занимает 7 с, а для последовательности из 4098 точек — 58 с.

Сопутствующие функции: FFT2, IFFT2, FFTSHIFT, Signal Processing Toolbox [1].

1. Signal Processing Toolbox User’s Guide. Natick: The MathWorks, Inc., 1993.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Fast Fourier transform

Syntax

Description

Y = fft( X ) computes the discrete Fourier transform (DFT) of X using a fast Fourier transform (FFT) algorithm.

If X is a vector, then fft(X) returns the Fourier transform of the vector.

If X is a matrix, then fft(X) treats the columns of X as vectors and returns the Fourier transform of each column.

If X is a mult >fft(X) treats the values along the first array dimension whose size does not equal 1 as vectors and returns the Fourier transform of each vector.

Y = fft( X , n ) returns the n -point DFT. If no value is specified, Y is the same size as X .

If X is a vector and the length of X is less than n , then X is padded with trailing zeros to length n .

If X is a vector and the length of X is greater than n , then X is truncated to length n .

If X is a matrix, then each column is treated as in the vector case.

If X is a multidimensional array, then the first array dimension whose size does not equal 1 is treated as in the vector case.

Y = fft( X , n , dim ) returns the Fourier transform along the dimension dim . For example, if X is a matrix, then fft(X,n,2) returns the n-point Fourier transform of each row.

Examples

Noisy Signal

Use Fourier transforms to find the frequency components of a signal buried in noise.

Specify the parameters of a signal with a sampling frequency of 1 kHz and a signal duration of 1.5 seconds.

Form a signal containing a 50 Hz sinusoid of amplitude 0.7 and a 120 Hz sinusoid of amplitude 1.

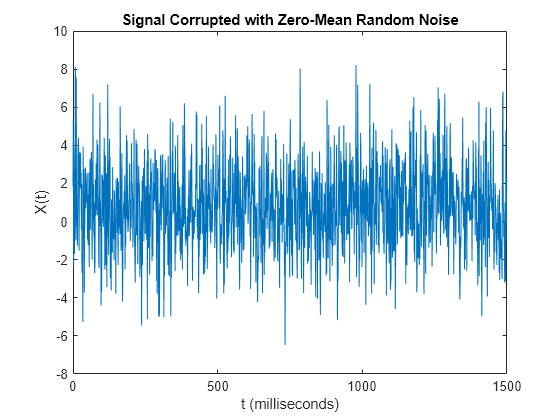
Corrupt the signal with zero-mean white noise with a variance of 4.

Plot the noisy signal in the time domain. It is difficult to >X(t) .

Compute the Fourier transform of the signal.

Compute the two-s >P2 . Then compute the single-s >P1 based on P2 and the even-valued signal length L .

Define the frequency domain f and plot the single-s >P1 . The amplitudes are not exactly at 0.7 and 1, as expected, because of the added noise. On average, longer signals produce better frequency approximations.

Now, take the Fourier transform of the original, uncorrupted signal and retrieve the exact amplitudes, 0.7 and 1.0.

Gaussian Pulse

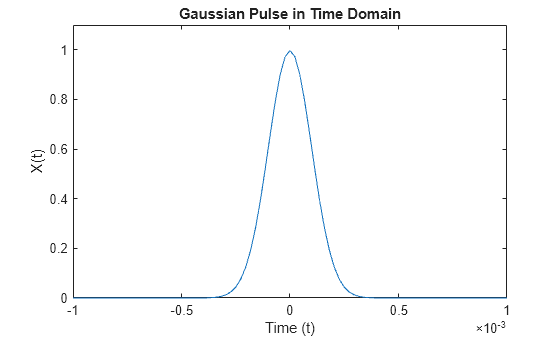
Convert a Gaussian pulse from the time domain to the frequency domain.

Define signal parameters and a Gaussian pulse, X .

Plot the pulse in the time domain.

To use the fft function to convert the signal to the frequency domain, first >X with trailing zeros in order to improve the performance of fft .

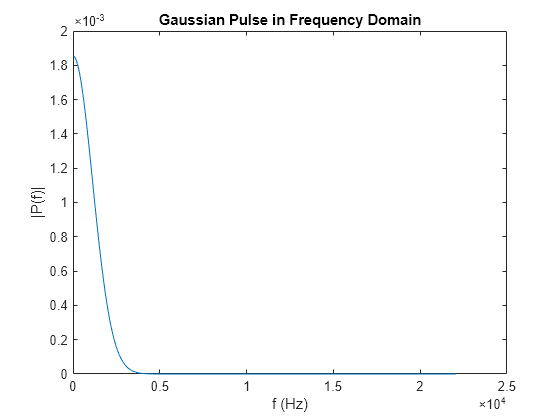
Convert the Gaussian pulse to the frequency domain.

Define the frequency domain and plot the unique frequencies.

Cosine Waves

Compare cosine waves in the time domain and the frequency domain.

Specify the parameters of a signal with a sampling frequency of 1kHz and a signal duration of 1 second.

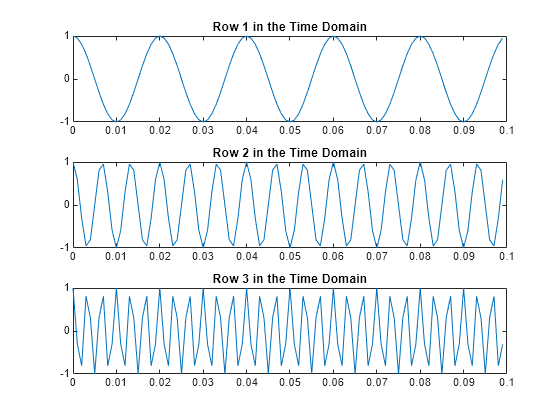
Create a matrix where each row represents a cosine wave with scaled frequency. The result, X , is a 3-by-1000 matrix. The first row has a wave frequency of 50, the second row has a wave frequency of 150, and the third row has a wave frequency of 300.

Plot the first 100 entries from each row of X in a single figure in order and compare their frequencies.

For algorithm performance purposes, fft allows you to pad the input with trailing zeros. In this case, pad each row of X with zeros so that the length of each row is the next higher power of 2 from the current length. Define the new length using the nextpow2 function.

Specify the dim argument to use fft along the rows of X , that is, for each signal.

Compute the Fourier transform of the signals.

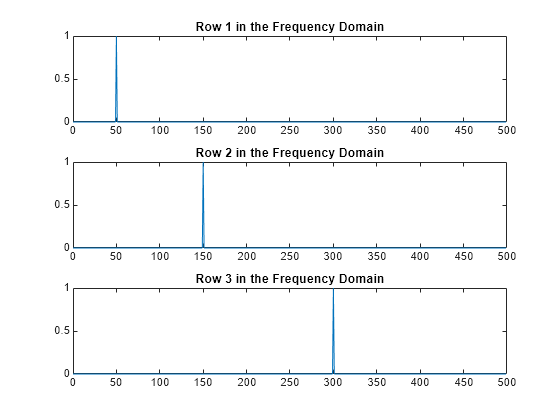
Calculate the double-sided spectrum and single-sided spectrum of each signal.

In the frequency domain, plot the single-sided amplitude spectrum for each row in a single figure.

Input Arguments

X — Input array
vector | matrix | multidimensional array

Input array, specified as a vector, matrix, or multidimensional array.

If X is an empty 0-by-0 matrix, then fft(X) returns an empty 0-by-0 matrix.

n — Transform length
[] (default) | nonnegative integer scalar

Transform length, specified as [] or a nonnegative integer scalar. Specifying a positive integer scalar for the transform length can increase the performance of fft . The length is typically specified as a power of 2 or a value that can be factored into a product of small prime numbers. If n is less than the length of the signal, then fft ignores the remaining signal values past the n th entry and returns the truncated result. If n is 0 , then fft returns an empty matrix.

Example: n = 2^nextpow2(size(X,1))

dim — Dimension to operate along
positive integer scalar

Dimension to operate along, specified as a positive integer scalar. If no value is specified, then the default is the first array dimension whose size does not equal 1.

fft(X,[],1) operates along the columns of X and returns the Fourier transform of each column.

fft(X,[],2) operates along the rows of X and returns the Fourier transform of each row.

If dim is greater than ndims(X) , then fft(X,[],dim) returns X . When n is specified, fft(X,n,dim) pads or truncates X to length n along dimension dim .

Output Arguments

Y — Frequency domain representation
vector | matrix | multidimensional array

Frequency domain representation returned as a vector, matrix, or multidimensional array.

If X is of type single , then fft natively computes in single precision, and Y is also of type single . Otherwise, Y is returned as type double .

The size of Y is as follows:

For Y = fft(X) or Y = fft(X,[],dim) , the size of Y is equal to the size of X .

For Y = fft(X,n,dim) , the value of size(Y,dim) is equal to n , while the size of all other dimensions remains as in X .

If X is real, then Y is conjugate symmetric, and the number of unique points in Y is ceil((n+1)/2) .

Data Types: double | single

По работе неоднократно сталкивался с необходимостью быстро определить наличие в сигнале гармонических составляющих. Часто для примерной оценки достаточно воспользоваться алгоритмом быстрого преобразования Фурье. Тем более, что его реализации есть практически во всех математических пакетах и библиотеках, да и собственноручно реализовать не составит особого труда. Между тем, опыт показывает, что, при всей своей простоте, метод начинает вызывать некоторые вопросы, когда возникает необходимость не просто посмотреть наличие дискреток в сигнале, но и выяснить их абсолютные значения, т.е. нормализовать полученный результат.

В этой статье я постараюсь объяснить, что же все-таки выдает в качестве результата fft (Fast Fourier transform) на примере MATLAB (и в качестве бонуса проведу небольшой ликбез по этому весьма полезному, на мой взгляд, языку).

MATLAB позволяет не заморачиваться с ручным удалением ненужных объектов, однако, при работе с более менее объемными массивами данных, имеет привычку капризничать и жаловаться на недостаток памяти. Для освобождения памяти используется процедура clear с указанием имени объекта, который необходимо удалить.

С этого и начнем. Так как все необходимое мы сгенерируем самостоятельно, можно смело удалять все, что накопилось в рабочем пространстве за активную сессию, просто добавив ключевое слово all:

clear all% Очистка памяти

Итак, прежде всего, зададим исходные данные для нашей модели. Фурье анализ идеально подходит для выделения гармонических сигналов на фоне помех. Для того чтобы продемонстрировать это, возьмем в качестве сигнала сумму некоторой постоянной и двух синусоид с разной частотой и амплитудой. Дисперсию шума возьмем в 3 раза больше амплитуды первой синусоиды. Так же зададим количество частотных полос, которые должен будет посчитать fft алгоритм. Точка с запятой в конце строк не обязательна, и если ее не ставить, результат вычисления функций и задания переменных будет дублироваться в командную строку, что можно использовать для отладки кода (однако, 512 значений сплошным полотном в командной строке вряд ли помогут вам, тем более что их вывод тоже занимает некоторое количество времени, так что все же лучше не забывать закрывать строки).

%% Параметры
Tm=5;% Длина сигнала (с)
Fd=512;% Частота дискретизации (Гц)
Ak=0.5;% Постоянная составляющая (Попугаев)
A1=1;% Амплитуда первой синусоиды (Попугаев)
A2=0.7;% Амплитуда второй синусоиды (Попугаев)
F1=13;% Частота первой синусоиды (Гц)
F2=42;% Частота второй синусоиды (Гц)
Phi1=0;% Начальная фаза первой синусоиды (Градусов)
Phi2=37;% Начальная фаза второй синусоиды (Градусов)
An=3*A1;% Дисперсия шума (Попугаев)
FftL=1024;% Количество линий Фурье спектра

MATLAB (Matrix Laboratory), как следует из названия, предназначен прежде всего для работы с массивами, практически все алгоритмы счета в нем оптимизированы для работы с векторами. Обилие удобных инструментов работы так же ненавязчиво подталкивает представлять как можно больше исходных данных в виде матриц. В частности, можно легко сгенерировать массив возрастающих (убывающих) величин с заданным шагом (1Fd в данном примере):

%% Генерация рабочих массивов
T=0:1/Fd:Tm;% Массив отсчетов времени

Случайный Гауссов шум задается функцией randn, результатом которой является массив размерности, заданной в ее параметрах. Для единообразия зададим его в виде строки (первый параметр 1) длиной соответствующей длине нашего массива отсчетов времен, что в свою очередь вычислим функцией length.

Noise=An*randn(1,length(T));% Массив случайного шума длиной равной массиву времени

Символ * используется для обозначения перемножения. Т.к. чаще всего действия производятся над векторами, то и умножение подразумевается векторное, но так же легко можно, не перегружая этот оператор, использовать его для поэлементного перемножения, добавив перед ним точку (.*). При умножении вектора на скаляр точка перед умножением не является обязательной. Также добавленная точка сделает поэлементным возведение в степень и деление.

Signal=Ak+A1*sind((F1*360).*T+Phi1)+A2*sind((F2*360).*T+Phi2);% Массив сигнала (смесь 2х синусоид и постоянной составляющей)

Теперь перейдем к тому, ради чего и затевалась данная статья — функции fft(). Аргументами стандартной функции MATLAB являются сам сигнал (в нашем случае Signal), размерность вектора-результата (FftL), а также измерение.
Последний аргумент определяет вдоль какого измерения располагается сигнал в случае если на вход подается многомерный массив (Иногда этот параметр ошибочно принимают за размерность преобразования Фурье, но это не так. Хотя в MATLAB есть реализации 2-хмерного fft2() и многомерного fftn() алгоритмов). Так как наш сигнал представляет собой вектор, то его вполне можно опустить.
Рассмотрим сначала сигнал без примеси шума. В качестве результата мы получим вектор комплексных чисел. Это и есть представление нашего сигнала в частотном домене в показательной форме. Т.е. модули этих комплексных чисел представляют амплитуды соответствующих частот (точнее полосы частот см. дальше), а аргументы – их начальные фазы. И если полученная фаза, однозначно вычисляется в радианах, то с амплитудой и частотами не все так просто.
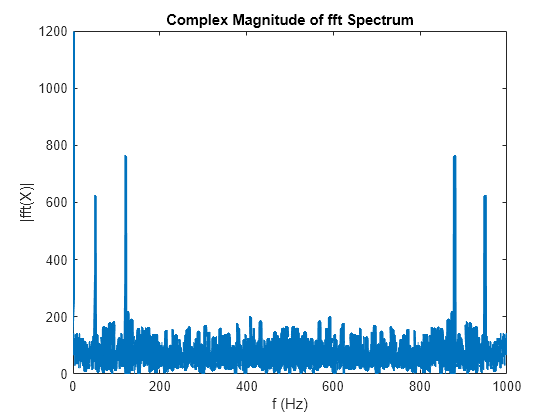
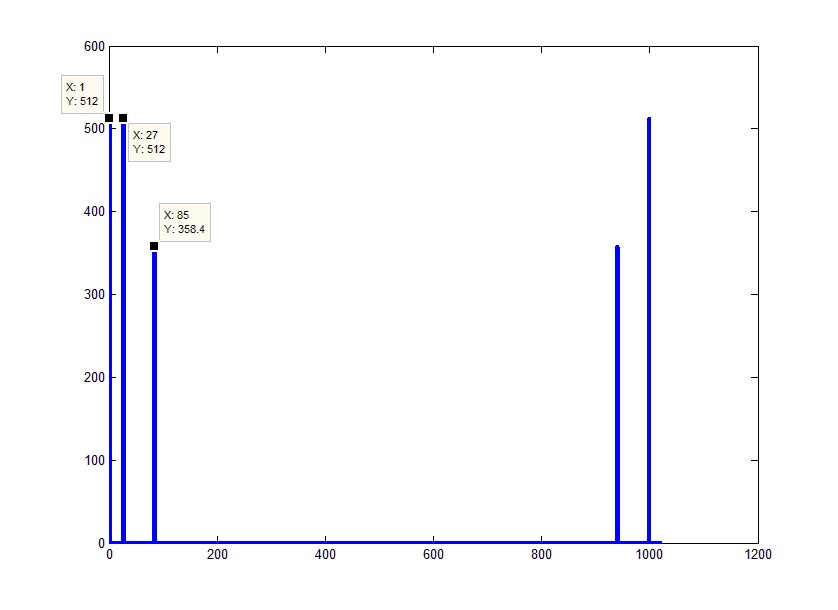
Например, если мы просто применим к нашему сигналу преобразование Фурье, и возьмем абсолютные значения вектора на выходе, то получим приблизительно следующую картинку:

Для построения двухмерных графиков удобно использовать функцию plot. Основные параметры, используемые в этой функции – одномерные массивы точек, первый задает ось ординат, второй – значение функции в соответствующих точках. Если передать только один массив, то он будет отображен с фиксированным шагом 1.
Если присмотреться к полученной картинке выяснится, что она несколько отличается от наших ожиданий. На приведенном графике 5 пиков вместо ожидаемых 3х (постоянная + 2 синусоиды), их амплитуды не совпадают с амплитудами исходных сигналов, и ось абсцисс вряд ли отображает частоты.

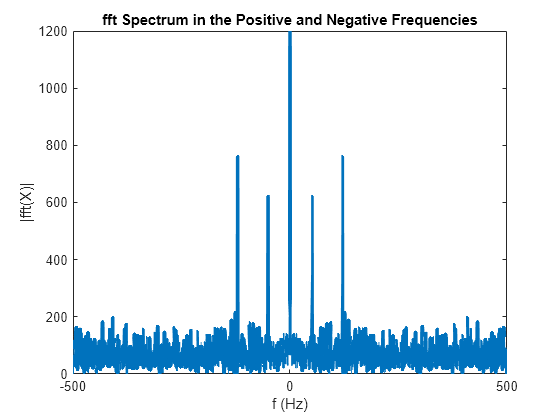
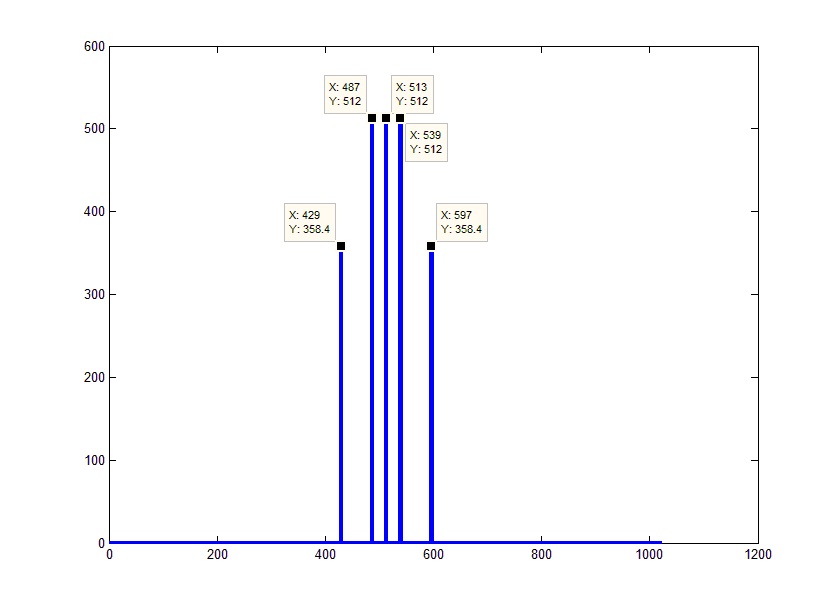
Прежде всего, следует учитывать, что счет алгоритма устроен таким образом, что перебираются не только положительные, но и отрицательные частоты и правая часть графика является «зеркальным» отображением реального спектра. Т.е. на самом деле 0 (которому соответствует постоянная часть сигнала) должен приходиться на середину массива. Ситуацию можно поправить, совершив циклический сдвиг на половину длины массива. Для этих целей, в MATLAB существует функция сдвига fftshift(), смещающая первый элемент в середину массива:

Теперь обратим внимание на ось значений.
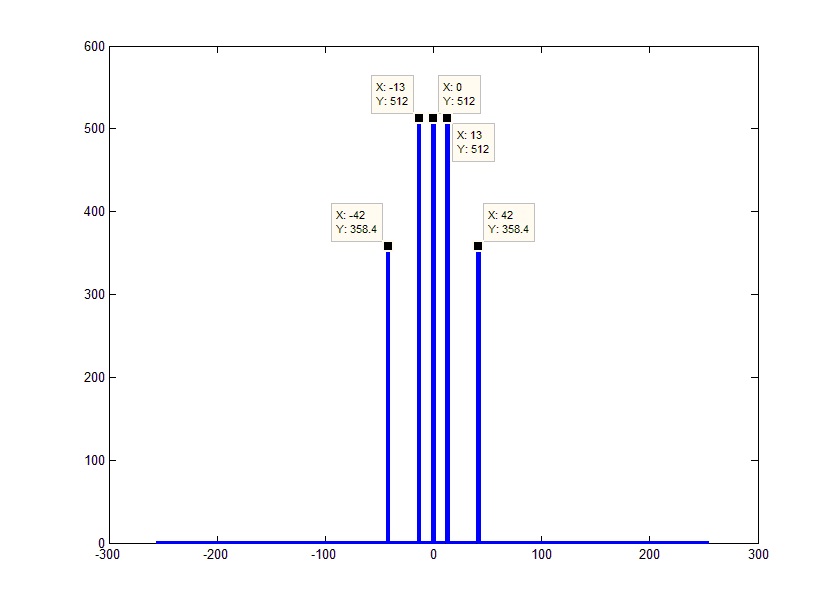
Согласно теореме отсчетов (так же известной как теорема Найквиста-Шеннона или более патриотично теорема Котельникова) спектр дискретного сигнала будет ограничен половиной частоты дискретизации (Fd). Или в нашем случае –Fd/2 слева и Fd/2 справа. Т.е. весь полученный массив покрывает Fd частот. Отсюда, учитывая что мы знаем (вернее даже самостоятельно задали в качестве параметра) длину массива, получим частоты в виде массива значений от –Fd/2 до Fd/2 с шагом Fd/FftL (на самом деле крайняя правая частота будет меньше границы на один отсчет т.е. Fd/2-Fd/FftL):

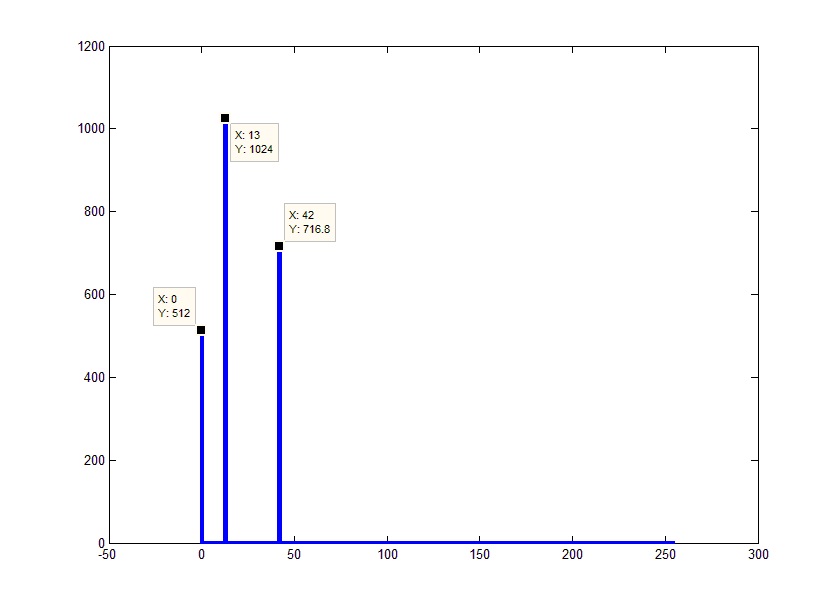
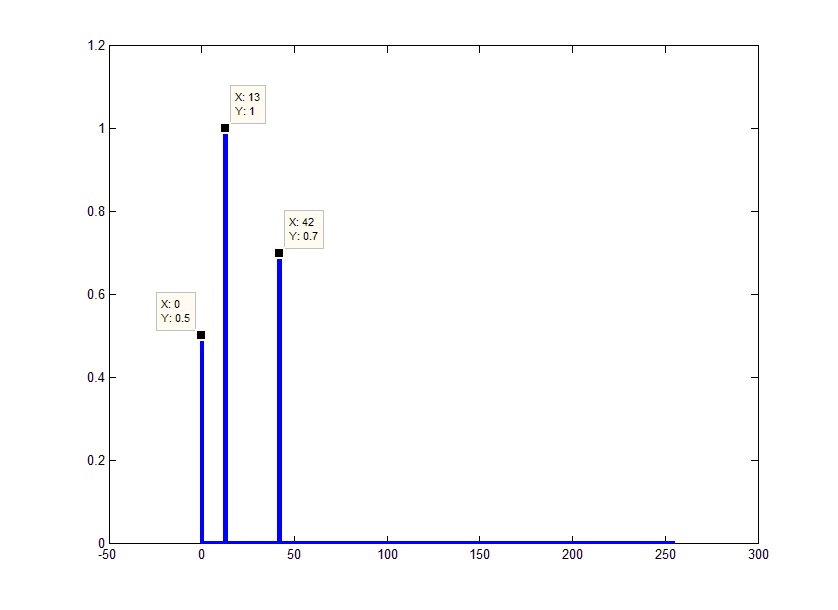
Если посмотреть на фазы частот, можно заметить, что они равны отрицательным фазам соответствующих отрицательных частот. Учитывая равенство амплитуд левой и правой частей спектра и соответствие их фаз с точностью до знака, весь спектр будет эквивалентен своей положительной части с удвоенной амплитудой. Исключение составляет только 0 элемент, который не имеет зеркальной половины. Таким образом, можно избавиться от «непонятных» и зачастую ненужных отрицательных частот. Это можно было сделать сразу просто отбросив конец исходного массива и помножив оставшиеся элементы на 2 (за исключением постоянной составляющей):

Теперь это уже похоже на тот результат, который мы ожидаем. Единственное, что смущает теперь – это амплитуды. С этим все достаточно просто. Т.к. быстрое преобразование Фурье фактически представляет собой суммирование сигнала перемноженного на ядро преобразования (комплексную экспоненту) для каждой из частот, то реальный результат будет меньше полученного ровно в количество суммирований (частот в результате), т.е. полученный результат надо разделить на количество элементов в результате (не забываем, что под результатом понимается весь ответ, вместе с отброшенной частью, т.е. наше заданное FftL):

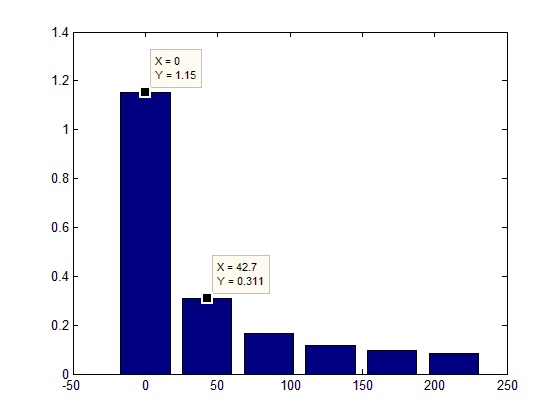
Стоит упомянуть еще одну вещь. В спектральном представлении вычисляется не значение сигнала на той частоте на которую попал алгоритм (как мы помним частоты следуют с шагом Fd/FftL), а значение в полосе (шириной равной шагу). Т.е. если в эту полосу попало несколько дискреток, то они суммируются. Для примера можно уменьшить количество линий в результате работы алгоритма:

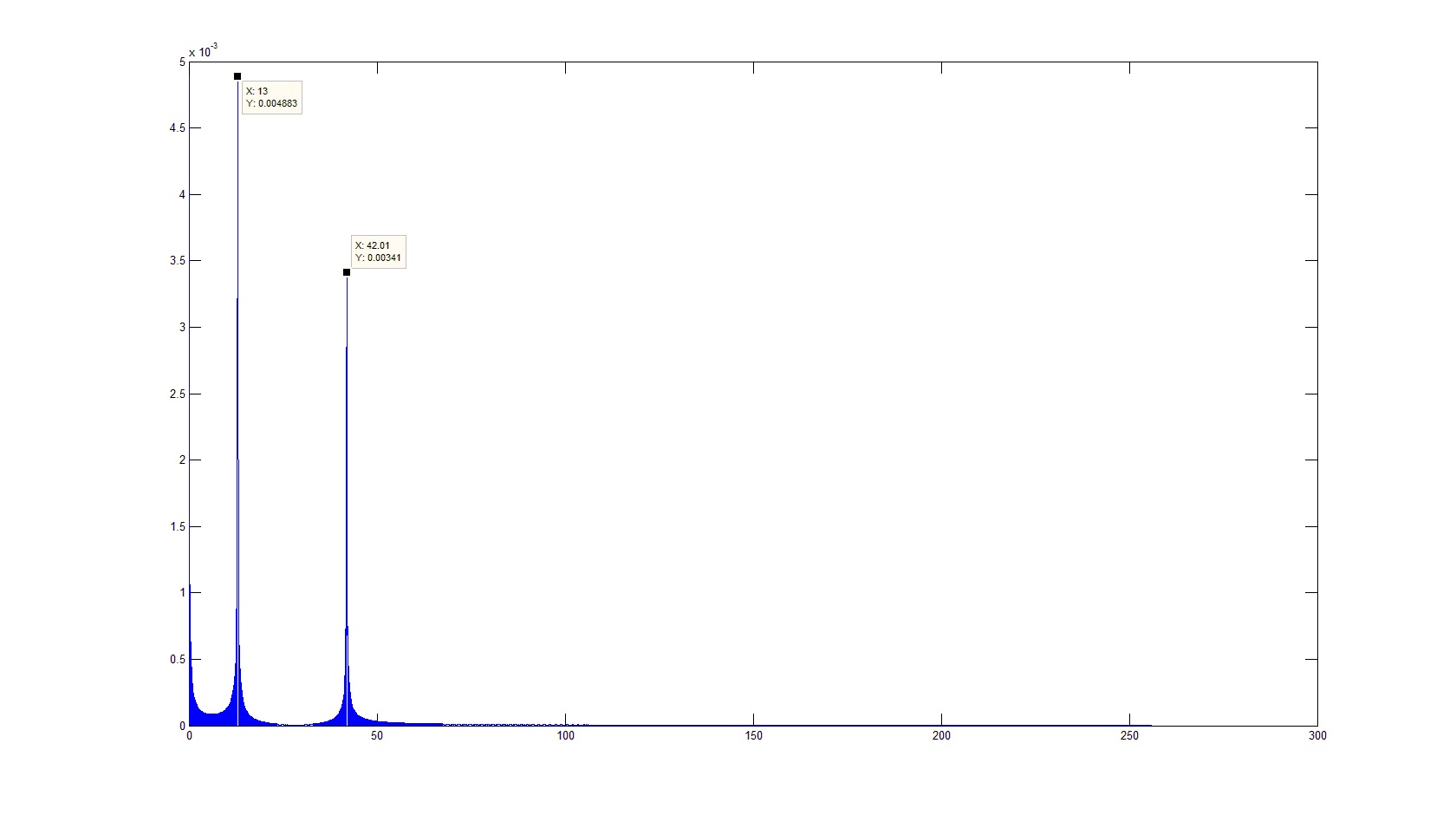
Однако это не означает, что стоит сразу бездумно увеличивать точность работы, т.к. это тоже приводит к негативным последствиям, т.к. если разрешение будет сопоставимо с частотой дискретизации сигнала, в спектр полезут гармоники «окна», которые имеют отношение не к реальному сигналу, а к его дискретному представлению:

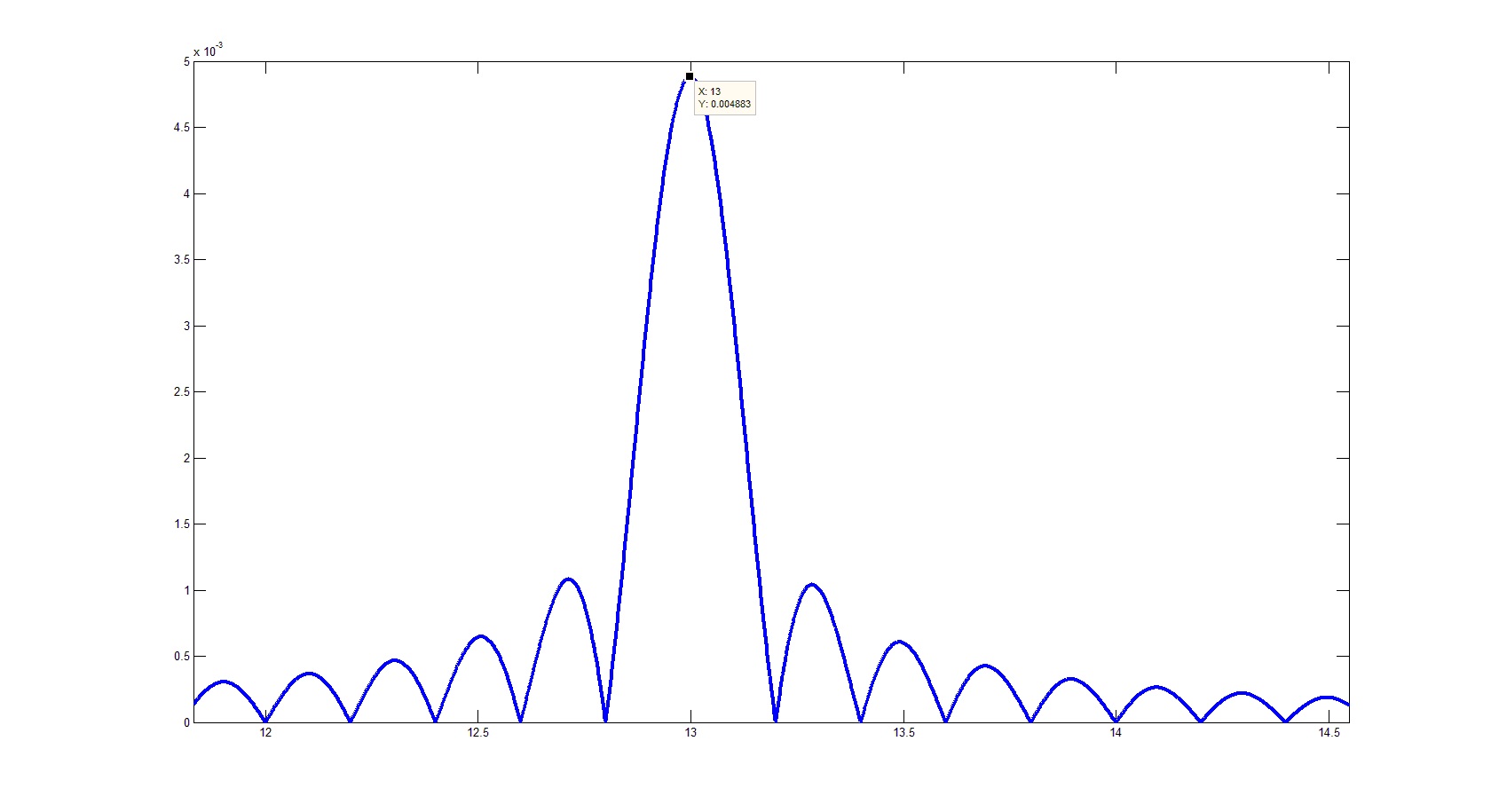
Или более близко окрестности одной из дискреток:

Код для нормировки fft будет выглядеть приблизительно следующим образом:

%% Спектральное представление сигнала
FftS=abs(fft(Signal,FftL));% Амплитуды преобразования Фурье сигнала
FftS=2*FftS./FftL;% Нормировка спектра по амплитуде
FftS(1)=FftS(1)/2;% Нормировка постоянной составляющей в спектре
FftSh=abs(fft(Signal+Noise,FftL));% Амплитуды преобразования Фурье смеси сигнал+шум
FftSh=2*FftSh./FftL;% Нормировка спектра по амплитуде
FftSh(1)=FftSh(1)/2;% Нормировка постоянной составляющей в спектре

Нам осталось только вывести результаты. Функция subplot позволяет разбить окно на несколько областей для отображения графиков.

%% Построение графиков
subplot(2,1,1);% Выбор области окна для построения
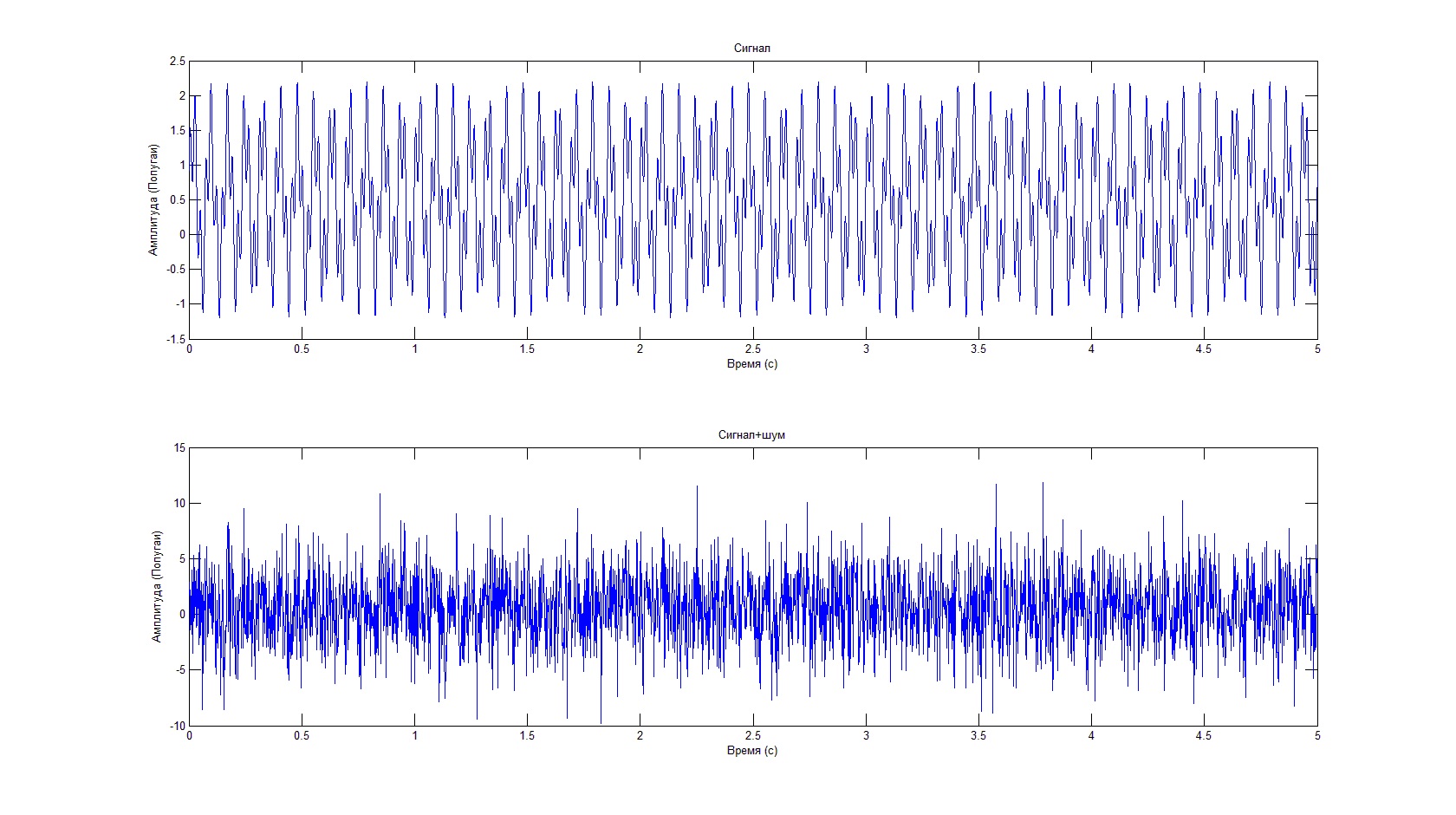
plot(T,Signal);% Построение сигнала
title(‘Сигнал’);% Подпись графика
xlabel(‘Время (с)’);% Подпись оси х графика
ylabel(‘Амплитуда (Попугаи)’);% Подпись оси у графика
subplot(2,1,2);% Выбор области окна для построения
plot(T,Signal+Noise);% Построение смеси сигнал+шум
title(‘Сигнал+шум’);% Подпись графика
xlabel(‘Время (с)’);% Подпись оси х графика
ylabel(‘Амплитуда (Попугаи)’);% Подпись оси у графика

F=0:Fd/FftL:Fd/2-1/FftL;% Массив частот вычисляемого спектра Фурье
figure% Создаем новое окно
subplot(2,1,1);% Выбор области окна для построения
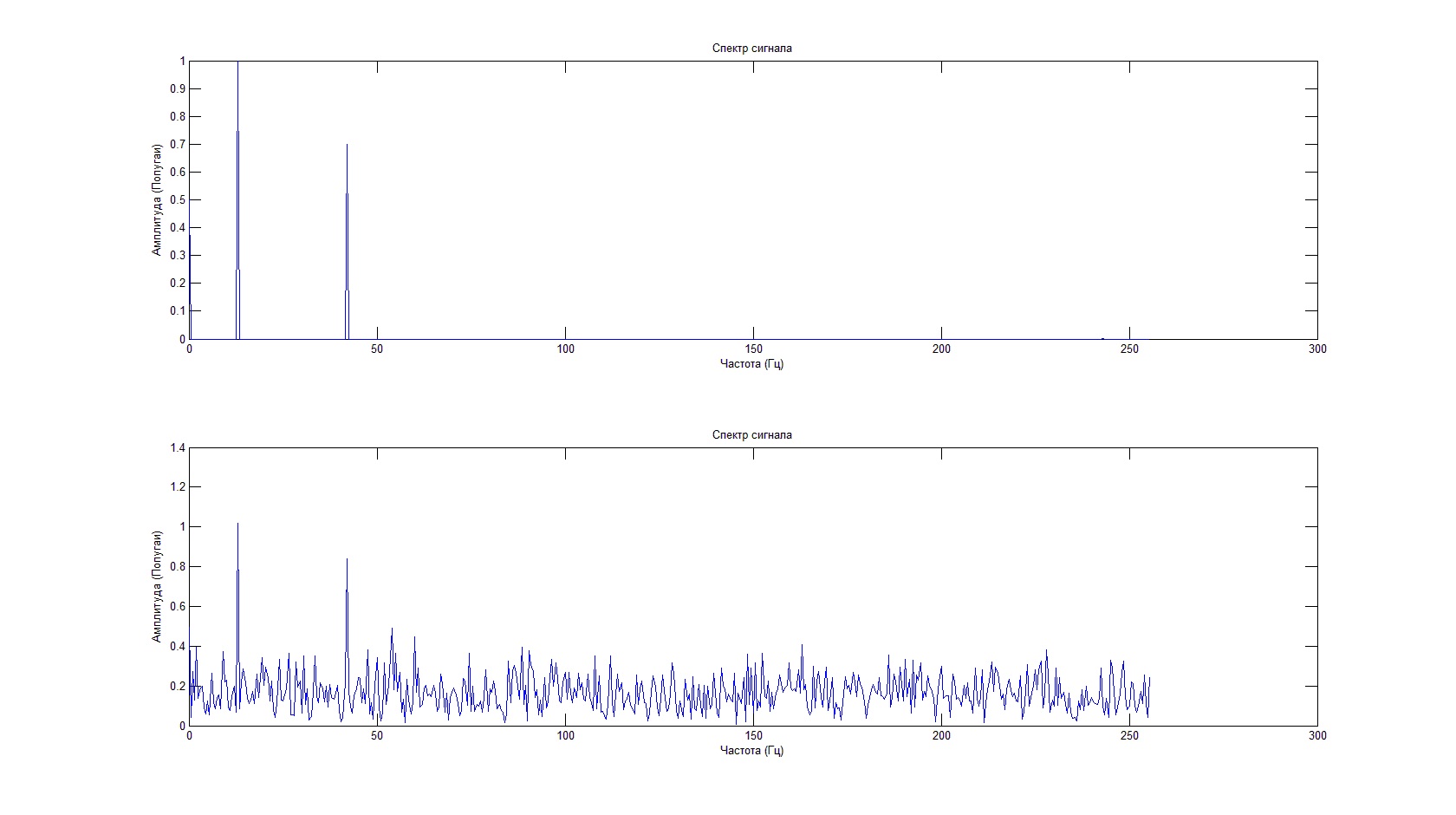
plot(F,FftS(1:length(F)));% Построение спектра Фурье сигнала
title(‘Спектр сигнала’);% Подпись графика
xlabel(‘Частота (Гц)’);% Подпись оси х графика
ylabel(‘Амплитуда (Попугаи)’);% Подпись оси у графика
subplot(2,1,2);% Выбор области окна для построения
plot(F,FftSh(1:length(F)));% Построение спектра Фурье сигнала
title(‘Спектр сигнала’);% Подпись графика
xlabel(‘Частота (Гц)’);% Подпись оси х графика
ylabel(‘Амплитуда (Попугаи)’);% Подпись оси у графика

Результат выполнения кода будет выглядеть следующим образом:

Несмотря на то, что полезного сигнала не видно на фоне шума, спектральная характеристика позволяет определить его частоту и амплитуду.