· логика, как наука;
· приоритет логических операций;
· тождественно истинные и тождественно ложные операции;
· основные законы алгебры логики;
· доказательство логических законов;
· простейшие преобразователи информации;
Если сложное высказывание истинно для всех значений входящих в него переменных, то такое высказывание называется ТОЖДЕСТВЕННО ИСТИННЫМ или тавтологией (обозначается константой 1).
НАПРИМЕР высказывание: "Демократ — это человек, исповедующий демократические убеждения" — всегда истинно, то есть является тавтологией.
Все математические, физические и др. законы являются тавтологиями. Например: (а+b) 2 = a 2 + 2ab + b 2
Прогноз погоды на завтра может быть, например, таким: "Дождь будет или дождя не будет". Такое предсказание будет всегда истинным, хотя вряд ли кого устроит. Его математическая запись:
(по закону исключенного третьего всегда должно быть истинным либо суждение, либо его отрицание).
Проверить, является ли сложное высказывание тождественно истинным, можно по таблице истинности.
Если сложное высказывание ложно при всех значениях входящих в него переменных, то такое высказывание называется ТОЖДЕСТВЕННО ЛОЖНЫМ (обозначается константой 0 ).
НАПРИМЕР, высказывание: "Сегодня среда, а это — второй день недели" является тождественно ложным. Тождественно ложным является и следующее высказывание: "Компьютер включен и компьютер не включен (выключен)". Математическая запись его такова:
(по закону противоречия: не могут быть одновременно истинны утверждение и его отрицание.)
Если значения сложных высказываний совпадают при всех возможных значениях входящих в них переменных, то такие высказывания называют РАВНОСИЛЬНЫМИ, ТОЖДЕСТВЕННЫМИ, ЭКВИВАЛЕНТНЫМИ
Упрощение сложных высказываний — это замена высказывания на равносильное ему на основе законов алгебры высказываний
ОСНОВНЫЕ ЗАКОНЫ (РАВНОСИЛЬНОСТИ) АЛГЕБРЫ ЛОГИКИ
· логика, как наука;
· приоритет логических операций;
· тождественно истинные и тождественно ложные операции;
· основные законы алгебры логики;
· доказательство логических законов;
· простейшие преобразователи информации;
При решении логических задач часто приходится упрощать формулы. Упрощение формул в булевой алгебре производится на основе эквивалентных преобразований, опирающихся на основные законы.
Законы логики высказываний — это такие выражения, которым всегда соответствует истинное высказывание, какие бы подстановки значений мы ни делали вместо переменных. В алгебре высказываний логические законы выражаются в виде формул.
1.1. Закон тождества:
— всякая мысль тождественна самой себе, то есть "А есть А", где А – любое высказывание.
2. Закон исключенного третьего:
— в один и тот же момент времени высказывание может быть либо истинным, либо ложным, третьего не дано. Истинно либо А, либо не А.
НАПРИМЕР. "Число 123 либо четное, либо нечетное, третьего не дано".
Закон исключенного третьего не является законом, признаваемым всеми логиками в качестве универсального закона логики. Этот закон применяется там, где познание имеет дело с жесткой ситуацией: либо-либо, истина-ложь. Там же где встречается неопределенность (например, в рассуждениях о будущем), закон исключенного третьего часто не может быть применен.
Рассмотрим следующее высказывание: "Это предложение ложно". Оно не может быть истинным, потому, что оно утверждает, что оно ложно. Но оно не может быть и ложным, потому что тогда оно было бы истинным. Это высказывание не истинно и не ложно, а потому нарушается закон исключенного третьего.
Парадокс (греч. paradoxos — неожиданный, странный) возникает из-за того, что предложение ссылается само на себя. Другим известным парадоксом является задача о парикмахере:
"В одном городе парикмахер стрижет волосы всем жителям, кроме тех, кто стрижет себя сам. Кто стрижет волосы парикмахеру?"
В нашей формальной системе нет возможности ввести такое ссылающееся само на себя истолкование, поэтому мы не можем выразить все возможные мысли и доводы.
3. Закон непротиворечия:
— не могут быть одновременно истинными суждение и его отрицание. То есть, если высказывание А — истинно, то его отрицание А должно быть ложным (и наоборот). Тогда их произведение будет всегда ложным.
Именно эта формула часто используется при упрощении сложных логических выражений.
Иногда этот закон формулируется так: два противоречащих друг другу высказывания не могут быть одновременно истинными.
ПРИМЕР. Е = "На Марсе есть жизнь и на Марсе жизни нет"
4. Закон двойного отрицания:
— если отрицать дважды некоторое высказывание, то в результате получается исходное высказывание.
НАПРИМЕР: А = "Неверно, что Матроскин не кот"
эквивалентно высказыванию А = "Матроскин — кот".
1. Используя алгебраические преобразования, доказать тождественную истинность или тождественную ложность формул:
1) 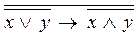
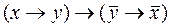
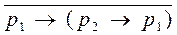
4) 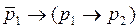
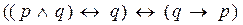
6) 
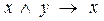

9) 
2. Доказать равносильности формул, не используя таблицы истинности:
1) 

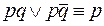

5) 
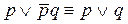

8) 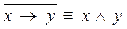
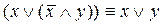
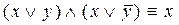
11) 

3. Упростить формулы:
1) 
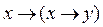


5) 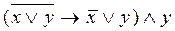
4. Привести следующие ниже формулы к базисам
1) 
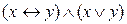
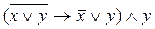
5. Развернуть конъюнкцию:
1) 
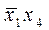
6. Развернуть дизъюнкцию:
1) 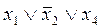

3.5.Функции алгебры логики.Нормальные формы логических
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9468 — 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Как и всякая логическая теория, логика высказываний решает две основные задачи: во-первых, выделяет среди класса формул множество своих законов и, во вторых, устанавливает логические отношения (прежде всего — отношение логического следования) между формулами формализованного языка.
Напомним, что законом логической теории является формула, которая принимает значение «истина» при любой допустимой в данной теории интерпретации нелогических символов, входящих в ее состав. Поэтому построение логики высказываний следует начать с вопроса
§4. Логические отношения между формулами о том, каким образом могут интерпретироваться нелогические символы ее языка, т. е. пропозициональные переменные (это единственный тип нелогических символов в языке пропозициональной логики).
Интерпретация пропозициональных переменных. Нелогические символы формализованных языков, как уже говорилось, являются параметрами некоторых выражений естественного языка. В частности, пропозициональные переменные — параметры простых высказываний.
Процедура интерпретации нелогических символов состоит в приписывании им значений. Тип значения каждого такого символа должен быть тем же самым, что и у соответствующих выражений естественного языка (т. е. выражений, параметрами которых данные символы являются).
Поскольку каждое простое высказывание либо истинно, либо ложно, то их параметрам — пропозициональным переменным — могут приписываться в качестве значений только «истина» или «ложь». Итак, существует две допустимых интерпретации каждой отдельно взятой пропозициональной переменной: 1) интерпретация, сопоставляющая ей значение «истина», 2) интерпретация, сопоставляющая ей значение «ложь».
Понятие интерпретации пропозициональных переменных можно распространить на случай, когда значения приписываются не одной, а некоторому числу п различных пропозициональных переменных, например рь р2. Рп-
Допустимой интерпретацией переменных рь р2. Рп является произвольный набор их значений, т. е. любая последовательность , где каждое aj есть либо «истина» (сокращенно и), либо «ложь» (сокращенно л), причем aj есть значение переменной pj.
Если последовательность рь р2. Рп состоит из одной переменной (т. е. если п= 1), то существует два набора значений: и . Компоненты этих одночленных последовательностей являются значениями pi при двух различных ее интерпретациях.
Если данная последовательность содержит две переменные (если п — 2), то наборами значений являются пары (всего их четыре):
Первая компонента пары указывает на значение pi, а вторая — на значение р2 при данной интерпретации.
Если последовательность содержит три переменные, то наборами значений будут тройки (всего их восемь):
Первая компонента тройки указывает на значение рь вторая — на значение р2, третья — на значение р3 при данной интерпретации.
Допустимые интерпретации переменных рь р2. рп могут быть представлены в виде таблицы: строчкам соответствуют различные интерпретации (наборы значений) этих переменных, а в столбцах записываются значения переменных при соответствующей интерпретации. Наборы значений удобно располагать в лексикографическом (алфавитном) порядке (как располагают слова в словаре). Составим подобные таблицы для одной, двух и трех переменных.
Число всех возможных наборов значений п переменных равно 2". Например, число допустимых интерпретаций четырех переменных равно 16, пяти — 32 и т. д.
Табличные определения пропозициональных связок. Следующий этап построения логической теории состоит в придании точных значений логическим символам алфавита. Напомним, что в нашем формализованном языке исходными логическими символами являются пропозициональные связки —I, &, v, z>. Эти связки, как уже говорилось, можно рассматривать как знаки функций истинности — функций, аргументами и значениями которых являются «истина» и «ложь».
Придать значение пропозициональной связке (в классической логике высказываний) — означает сопоставить ей