На этой странице вы найдете решения типовых задач по теории вероятностей на использование теорем Лапласа (интегральной и локальной, еще их называют формулами Муавра-Лапласа) и их следствия.

Данные приближенные формулы применяются, когда мы по-прежнему решаем задачи схемы независимых испытаний Бернулли (примеры тут), но речь идет уже об очень большом числе испытаний (стандартные условия $n>100$, $np>20$). Непосредственные вычисления по формуле Бернулли трудоемки, и мы прибегаем к удобным и простым теоремам Муавра-Лапласа.

Формулы Муавра-Лапласа

Рассмотрим $n$ независимых испытаний, в каждом из которых событие может произойти с одной и той же вероятностью $p$. Тогда при больших $n$ вероятности можно вычислять по приближенным формулам Муавра-Лапласа.

Вероятность того, что событие наступит в точности $k$ раз, можно вычислить по формуле (локальная теорема Лапласа):

Значения функции $phi (x) =frac<1><sqrt<2pi>> e^<-x^2/2>$ берутся из таблиц.

Вероятность того, что событие наступит от $k_1$ до $k_2$ раз, можно вычислить по формуле (интегральная теорема Лапласа):

$$ P(k_1 le X le k_2) approx Phi left( frac<sqrt>
ight) — Phi left( frac<sqrt>
ight) $$

Здесь $Phi(x)$ — нормированная функция Лапласа (ее значения берутся из таблиц)

Еще теорию по этой теме вы найдете в онлайн-учебнике.

Примеры решений

Локальная теорема Лапласа

Задача 1. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что среди 100 новорожденных окажется 50 мальчиков.

Задача 2. Вычислительное устройство состоит из 1000 элементов, работающих независимо друг от друга. Вероятность отказа каждого элемента за смену равна $р$. Найти вероятность, что за смену откажут $m$ элементов.
$р=0,024, m=6$.

Задача 3. На конвейер за смену поступает 300 изделий. Вероятность того, что поступившая на конвейер деталь стандартна, равна 0,75. Найти вероятность того, что стандартных деталей на конвейер за смену поступило ровно 240.

Задача 4. Вероятность поражения мишени стрелком при одном выстреле равна 0,8 Найти вероятность того, что при 100 выстрелах стрелок поразит мишень ровно 75 раз. Найти наивероятнейшее число попаданий в цель.

Задача 5. Игральную кость подбрасывают 500 раз. Какова вероятность того, что цифра 1 при этом выпадет 50 раз?

Интегральная теорема Лапласа

Задача 6. В жилом доме имеется $n$ ламп, вероятность включения каждой из них в вечернее время равна 0,5. Найти вероятность того, что число одновременно включенных ламп будет между $m1$ и $m2$. Найти наивероятнейшее число включенных ламп среди $n$ и его соответствующую вероятность.
$n = 6400, m1 = 3120, m2 = 3200$.

Задача 7. Найти вероятность того, что если бросить монету 200 раз, то орел выпадет от 90 до 110 раз.

Задача 8. Вероятность изготовления годной детали равна 0,8. Произведено 500 деталей. Какое число годных деталей вероятнее получить: а) менее 390; б) от 390 до 410?

Задача 9. Стоматологическая клиника распространяет рекламные листовки у входа в метро. Опыт показывает, что в одном случае из тысячи следует обращение в клинику. Найти вероятность того, что при распространении 50 тыс. листков число обращений будет:
А) равно 41,
Б) находиться в границах от 36 до 47.

Задача 10. Страховая компания заключила 40000 договоров. Вероятность страхового случая по каждому из них в течение года составляет 2%. Найти вероятность, что таких случаев будет не более 870.

Решебник по теории вероятностей

Тысячи решенных и оформленных задач на формулу Лапласа и другие темы:

17 сентября 2015

  • Материалы к уроку
  • Таблица значений функции Лапласа

Данная теорема является дальнейшим развитием схемы Бернулли и позволяет работать с диапазонами: какова вероятность, что число успехов будет лежать в пределах указанного отрезка.

. Пусть число испытаний $n$ достаточно велико, а вероятность успеха $0 lt ,p, lt 1$. Пусть также$q=1-p$ — вероятность неудачного испытания. Тогда вероятность того, что число успехов будет лежать в пределах от $<_<1>>$ до $<_<2>>$, можно примерно посчитать по формуле:

Функция $Phi left( x
ight)$ называется функцией Лапласа и содержит в себе интеграл, который не считается напрямую. Как следствие, значения этой функции сведены в таблицу, которую можно загрузить прямо на этой странице.

Разумеется, в таблице приведены не все возможные значения. Для больших значений $x$ (скажем, для $x gt 6$ ) считают, что $Phi left( x
ight)approx 0,5$. Кроме того, функция Лапласа является нечётной, поэтому из неё можно выносить знак «минус»:

[Phi left( -x
ight)=-Phi left( x
ight)]

Это прямо следует из определения, в котором присутствует определённый интеграл.

Что такое "интегральная теорема Муавра-Лапласса"?

Сегодня мы разберем интегральную теорему Муавра-Лапласа. Это «старшая сестра» второй версии теоремы Муавра-Лапласа, разобранной в прошлом уроке. Во-первых, разберемся, зачем вообще нужна еще одна теорема — интегральная.

Допустим, у нас есть 1000 изделий, о которых известно, что там в среднем есть 10% брака. Однако это не означает, что в партии из 1000 изделий будет ровно 100 бракованных изделий, скорее всего, их будет 101-102 или 98, но не 100. Вероятность того, что будет ровно 100, легко считается при помощи более легкой теоремы Муавра-Лапласа, и вы можете сами убедиться, что она будет велика. В этом случае возникает вопрос: «Какова тогда вероятность, что деталей будет от 95 до 105, либо от 50 до 150?». Считать такую конструкцию при помощи первой версии теоремы Муавра-Лапласса крайне сложно, потому что нам придется отдельно посчитать, какова возможность того, что бракованных изделий будет 50, 51, 51 и так до 150, т.е. сто отдельных однотипных вычислений. Это очень трудоемко и бессмысленно. Вот именно в таких примерах нам на помощь приходит интегральная теорема Муавра-Лапласа. С назначением самой интегральной теоремы все ясно, теперь давайте разберемся с ее формулой.

Вероятность того, что при $n$-испытаниях количество успешных испытаний будет в пределах от $<_<1>>$ до $<_<2>>$ выражается следующей формулой:

Сама же функция $F$ называется функцией Муавра-Лапласа, и выглядит она следующим образом:

Сразу же скажу, что данный интеграл «красиво» не считается, поэтому вместо красивого интегрирования у вас всегда будет в распоряжении таблица значений функции Лапласа, и с помощью этой таблицы, а также некоторых способов, которые мы разберем чуть позже в этом уроке, мы и будем решать все примеры на данную интегральную теорему.

Разумеется, возникает вопрос «А что это за буквы такие — $n$, $q$, $p$?».

С $n$, я думаю, все понятно — это число испытаний.

$p$ — это вероятность успеха в каждом конкретном испытании.

$q$ — по аналогии с формулой Бернули это вероятность провала, т.е. неуспеха в каждом конкретносм испытании. Считатеся она по очень простой формуле:

Надеюсь, с буквами теперь понятно, поэтому перейдем к решению конкретных примеров.

Задача № 1

Начнем мы с довольно простой задачи, однако уже на ее примеры мы познакомимся с особенностями применения интегральной теоремы Муавра-Лапласса.

Известно, что в среднем 5% студентов носят очки. Какова вероятность того, что из 200 студентов, находящихся в аудитории, окажется не менее 10%, носящих очки?

В первую очередь, давайте запишем саму интегральную теорему Муавра-Лапласса:

При этом полезно помнить еще одну формулу:

Собственно, из-за этого интеграла, присутствуещего в функции Муавра-Лапласса, сама теорема и называется интегральной.

При первом взгляде на эту интегральную теорему многие ученики приходят в шок — уж больно много здесь разных конструкций, корней, вычислений и т.д. На самом деле, все очень просто, и сейчас вы сами в этом убедитесь.

Для начала давайте выпишем все значения. Итак, нам известно следующее:

  • Всего студентов 200 — $n=200$;
  • Вероятность попадания студента, который носит очки — $p=0,05$;
  • Вероятность того, что студенты не носят очки будет равна $1-0,05=0,95$.

Далее мы можем найти $sqrt$:

Разумеется, такие вычисления выполняются на калькуляторе.

Кроме того, в нашей формуле, в интегральной теореме Муавра-Лапласса, мы наблюдаем выражение $np$ — произведение количества испытаний на вероятность успеха:

Давайте перепишем формулу с учетом всех фактов:

[=Fleft( 61,7
ight)-Fleft( 3,25
ight)]

И вот здесь нас поджидает первая проблема: если мы посмотрим на таблицу значений, то значение $3,25$ здесь еще присутствует, но вот числа от $60$ и более здесь вообще не представлены. Для решения этого вопроса предлагаю взглянуть на исходную формулу Муавра-Лапласса:

При больших «иксах» $<^<-frac<<^<2>>><2>>>$ будет очень маленьким числом, т.е. возрастание $x$ дает очень маленькую, стремящуюся к «нулю» добавку к вероятности. Поэтому для всех «иксов», начиная от шести и более примерно считается, что значение функции Лапласса равно $0,5$. $$ $$

Итак, продолжим наше решение:

Нюансы решения

Как видите, ничего сверхъестественного. Все применение интегральной теоремы Муавра-Лапласса сводится к следующему:

  1. Аккуратно выписать все значения: число испытаний, вероятность и «единицу» «минус» вероятность.
  2. Посчитать корни и величины.
  3. Пробежаться глазами по таблице и найти значение функции в тех точках, которые мы получили.

Однако, как вы понимаете, это была самая простая задача — существуют гораздо более сложные и навороченные. И один из самых «противных» типов заданий на применение интегральной теоремы Муавра-Лапласса состоит в том, что общая вероятность, которую мы обычно рассчитываем по формуле, нам известна, а необходимо найти либо $<_<1>>$, либо $<_<2>>$. Вот именно сейчас такую задачу мы и решим.

Самое обидное, что именно такие чаще всего и попадаются на всяких контрольных, зачетах и экзаменах. Они будут вам встречаться на исследованиях, где необходимо определить какую-нибудь статистическую величину. Поэтому именно сейчас мы попытаемся решить такую задачу.

Задача № 2

Театр, вмещающий 1000 человек, имеет два разных входа, каждым из которых любой зритель может воспользоваться с равной вероятностью. Около каждого входа имеется свой гардероб. Сколько мест должно быть в каждом гардеробе, чтобы с вероятностью в 0,99 любой зритель смог раздеться в том гардеробе, в который он обратился сразу после входа в театр.

Я думаю, очевидно, что в данной задаче общее количество испытаний, т.е. человек, которые придут в театр, не более 1000 — $n=1000$.

Всего входов два, при этом в каждый с одинаковой вероятностью входит один и тот же человек — $p=frac<1><2>$.

Кроме того, общая возможность того, что при 1000 испытаний количество успеха попадет в искомый нами диапазон, равно 0,99 — $<

_<1000>>left( <_<1>>;<_<2>>
ight)=0,99$. Остается разобраться с числами $<_<1>>$ и $<_<2>>$, т.е. границами диапазона. $<_<1>>$ — наименьшее количество людей, которые могут обратиться в данный гардероб. Очевидно, будет «ноль», потому что меньше нуля прийти не может — $<_<1>>=0$. Остается вопрос: «Чему равно $<_<2>>$?». Именно это нам и нужно найти по условию.

Опять запишем интегральную теорему Муавра-Лапласса:

Подставим все полученные числа в формулу, с учетом того, что $<_<1>>=0$:

Теперь внимательно посмотрим на эту формулу. Отдельно посчитаем значение функции Муавра-Лапласса в следующей точке:

[Fleft( frac<-500> <15,8>
ight)=-Fleft( 31,6
ight)=0,5]

Итого переписывая, мы получаем:

Единственный способ, при помощи которого можно решить этот пример — это взять таблицу значений функции Муавра-Лапласса и посмотреть, когда она равна $0,49$, при каком $x$. Проблема состоит в том, что точного значения мы не найдем. Однако есть значение функции Муавра-Лапласса в точках $2,32$ и $2,34$ :

[Fleft( 2,32
ight)=0,48983]

[Fleft( 2,34
ight)=0,49036]

Где-то между ними лежит наша искомая величина $0,49$. А между числами $2,32$ и $2,34$ лежит величина $2,33$. Так и запишем:

Теперь нам осталось решить простейшее уравнение:

Каверзные вопросы

Подождите, есть несколько вопросов. Во-первых, почему мы так легко вынесли «минус» из функции Лапласса наружу, а во-вторых, почему мы постоянно пользуемся калькулятором?

Давайте для начала посмотрим на формулу функции Муавра-Лапласса:

Это, прежде всего, интеграл от «нуля» до $x$ в прелах четной функции, поэтому если перед $x$ внезапно появится «минус», мы можем поменять местами верхние и нижнее пределы интегрирования, при том перед самим интегралом также появится знак «минус», и больше никаких изменений не будет. Это одно из ключевых свойств определенного интеграла.

Кроме того, в таблице значений все аргументы функций приведены именно в виде десятичных дробей, поэтому считая значение функции, мы просто обязаны перевести то, что стоит у нас внутри скобок, в десятичную дробь, в том числе с помощью калькулятора.

В заключение посмотрим еще одну задачку, в которой мы не только еще раз отработаем использование стандартной формулы, но и вспомним, что такое вторая версия теоремы Муавра-Лапласса, отличная от интегральной, и в каких ситуациях она применяется.

Задача № 3

Радиотелеграфная станция передает цифровой текст. В силу наличия помех каждая цифра независимо от других может быть неправильно принята с вероятностью 0,01. Найдите вероятность того, что в принятом тексте, содержащем 1100 цифр, будет:

б) менее 20 ошибок.

Решение пункта б)

Что касается б), то тут все вполне очевидно — это чистейшая теорема Муавра-Лапласса, причем интегральная. Так и запишем:

Теперь запишем интегральную формулу Муавра-Лапласса:

Осталось подставить числа в формулу:

[=Fleft( 2,42
ight)+Fleft( 3,33
ight)=]

Решение пункта а)

А теперь давайте разберемся с пунктом а). В нем от нас требуется, чтобы при тех же исходных данных, вычислить, что в итоге появится ровно 15 ошибок.

Очевидно, что это идеальная задача для применения второй версии теоремы Муавра-Лапласса — не интегральной. Давайте я ее запишу:[]

Выпишем известные данные:

[<

_<1100>>left( 15
ight)approx frac<1><3,3>cdot varphi left( frac<15-11> <3,3>
ight)approx 0,303cdot varphi left( 1,212
ight)approx ]

[approx 0,303cdot 0,1919approx 0,058]

Ключевые моменты

Вот и все, что я хотел вам рассказать об интегральной теореме Муавра-Лапласса, такой, на первый взгляд сложной, но очень простой на практике. Все, что вам необходимо — это

  1. Знать сами формулы для обеих теорем Муавра-Лапласса, в том числе, интегральной.
  2. Грамотно считать корни и элементы $np$, которые являются матожиданием.

В ближайшее время я размещу на своем сайте целый комплект задач, посвященный теоремам Муавра-Лапласса, в том числе, интегральной. Поэтому присоединяйтесь к нам на YouTube, ставьте лайки и пишите комментарии. До новых встреч!

Приложения интегральной теоремы Муавра-Лапласа

1. Закон больших чисел (неравенство Бернулли). .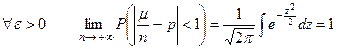

Неравенство Бернулли позволяет использовать построения теории вероятностей при решении многих задач естествознания и техники.

Проводится n независимых испытаний, при каждом из которых вероятность наступления события P(А)=р.

1. Чему равна вероятность того, что частота наступления события А отклонится от вероятности р не более чем на α?

.

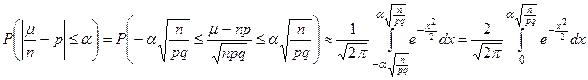
2. Какое наименьшее число испытаний нужно произвести для того, чтобы с вероятностью, не меньшей β, частота отклонялась от вероятности не больше чем на α?

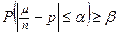
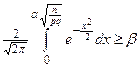
Нужно определить n из неравенства . Вероятность, стоящую в левой части неравенства, приближённо заменим по теореме Муавра-Лапласа интегралом. В результате для определения n получится неравенство .

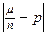
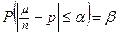
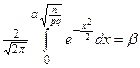
3. При данной вероятности β и числе испытаний n требуется определить границу возможных изменений . Другими словами, зная β и n, нужно найти α, для которого . Применение интегральной теоремы Лапласа даёт для определения α уравнение .

Определение. Функция 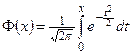называется функцией Лапласа.

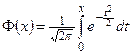
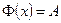
Замечание.Так как в конечном виде через элементарные функции не выражается, то для вычисления , а также для решения обратной задачи – вычисления х по заданному А, используют специальные таблицы и свойства функции Лапласа.

3. .

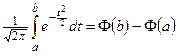
Пример 2. Вероятность изделию некоторого производства оказаться бракованным равна 0б005. Чему равна вероятность того, что из 10000 наудачу взятых изделий бракованных изделий окажется не более 70?

Решение. n=10000, p=0,005. Поэтому по формуле (1) находим вероятность того, что число бракованных изделий окажется не больше 70, равна сумме вероятностей числу бракованных изделий оказаться равным 1, 2, 3, …, 70. Таким образом: .

По интегральной теореме Муавра-Лапласа

Замечание 1. Значения (…) в таблице значений функции Лапласа нет. Все значения, большие 5, заменяются значением при х=5, погрешность при этом составляет менее .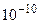

Замечание 2.Если значения р и q не слишком близки к 0 и 1, то интегральная теорема Муавра Лапласа даёт удовлетворительные результаты, но при р и q близких к 0 или 1это представление работает плохо. Для того, чтобы в этом случае теорема Муавра-Лапласа дала хороший результат, требуется, чтобы n было очень велико.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8835 — | 7551 — или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно