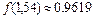Pers.narod.ru. Обучение. Компактно считаем полином Лагранжа в Excel
Теоретическое описание и формулу полинома Лагранжа можно найти, например, здесь. Численные методы сейчас многие изучают тоже в Excel, в котором готовой функции построения интерполяционного многочлена (канонического полинома, полинома Лагранжа или полинома Ньютона) нет.
В инете — либо странные советы (например, построить график и использовать в настройках рядов данных графика функцию "линия тренда" — совершенно не то, если понимать, что в Excel доступны только сглаживающие, а не интерполирующие кривые), либо дикие решения с расчётом каждой разности xi-xj в отдельной ячейке и т.п.
Меж тем, всё очень просто и считается так, как показано на скрине.
Перед вводом формулы 1 надо выделить ячейки C2:C9, а потом уже вводить, как обычно и делается при работе с формулами диапазонов.
Для другого количества точек будут просто другие диапазоны в первой и второй формулах.

Пример. Построить многочлен Лагранжа 3-й степени, если заданы значения в 4-х узлах интерполяции:
| xi | -1 |
| yi | -1 |
Решение: Многочлен Лагранжа для четырех узлов интерполяции запишется так –
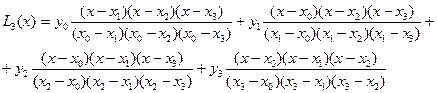
Для вычисления значения многочлена в точке х можно воспользоваться электронными таблицами Exel (рис. 18). В ячейки А3:А6 и В3:В6 записываются соответствующие значения yi и xi. В ячейки С3:С6 – формулы для вычисления pi(x). В столбце D3:D7 вычисляется значение
| A | B | C | D |
| Вычисление многочлена Лагранжа | |||
| yi | xi | X | |
| -1 | -1 | =$D$2-B3 | =A3*(C5*C4*C6)/((B3-B4)*(B3-B5)*(B3-B6) |
| Копировать С3 в С6 | =A4*(C3*C5*C6)/((B4-B3)*(B4-B5)*(B4-B6) | ||
| =A5*(C3*C4*C6)/((B5-B3)*(B5-B4)*(B5-B6) | |||
| =A6*(C3*C4*C5)/((B6-B3)*(B6-B4)*(B6-B5) | |||
| Значение L3(x) | =СУММ(D3:D6) |
4 .Варианты лабораторных работ для решения алгебраических и трансцендентных уравнений .
Задания: На отрезке [-10, 10] определить корни следующих уравнений:
8. x^3 – 0,1x^2+0,4x-1,5=0
23. 
24. 
5. Варианты лабораторных работ для решения систем линейных алгебраических уравнений .
Найти решение системы линейных уравнений методом итераций с точностью е=10-3:
Варианты лабораторных работ для решения систем линейных алгебраических уравнений .
Найти решение системы линейных уравнений методом итераций с точностью е=10-3:
Варианты лабораторных работ для решения систем линейных алгебраических уравнений .
Найти решение системы линейных уравнений методом итераций с точностью е=10-3:
Варианты лабораторных работ для решения систем линейных алгебраических уравнений .
Найти решение системы линейных уравнений методом итераций с точностью е=10-3:
6. Варианты лабораторных работ для решения задач интерполирования .
Задания. Построить интерполяционный полином Лагранжа L(x). Вычислить приближенное значение F(x) с помощью L(x) в точке х= 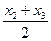
| xk | 0.1 | 0.3 | 0.4 | 0.6 |
| yk | -0.1 | 0.5 | 0.8 | 1.7 |
| xk | -1 | -0.5 | 0.1 | 0.4 |
| yk | 1.0 | 2.2 | 1.7 | 0.8 |
| xk | 1.1 | 1.2 | 1.4 | 1.7 |
| yk | -2.0 | -1.8 | -1.3 | -1.0 |
| xk | -1.0 | -0.5 | 0.3 | |
| yk | 0.9 | 0.7 | 0.4 | 0.8 |
| xk | 3.2 | 3.4 | 3.7 | |
| yk | -14 | -10 | -8 | -12 |
| xk | 1.0 | 3.0 | 7.0 | 10.0 |
| yk | 0.3 | 0.7 | 0.9 | 1.0 |
| xk | -10.0 | -8.0 | -5.0 | -2.0 |
| yk | 6.0 | 3.0 | 0.0 | -4.0 |
| xk | 2.0 | 3.0 | 5.0 | 6.0 |
| yk | 0.7 | 1.2 | 2.2 | 3.0 |
| xk | 0.7 | 1.2 | 2.2 | 3.0 |
| yk | 0.8 | 1.0 | 1.3 | 1.2 |
| xk | ||||
| yk | 0.01 | 0.03 | 0.08 | 0.12 |
| xk | -10 | -8 | -5 | -2 |
| yk | -2 | |||
| xk | ||||
| yk | 0.1 | -0.2 | -0.3 | |
| xk | 2.0 | 3.2 | 4.2 | 5.6 |
| yk | -15 | -10 | -8 | -6 |
| xk | -4 | -3 | -2 | |
| yk | ||||
| xk | 10.5 | 11.5 | 12.5 | 13.0 |
| yk | -6 | -7 | -5 |
6. Варианты лабораторных работ для решения задач интерполирования .
Задания. Построить интерполяционный полином Лагранжа L(x). Вычислить приближенное значение F(x) с помощью L(x) в точке х= 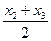
| xk | ||||
| yk | -3 | -2 | ||
| xk | -0.3 | 0.1 | 0.0 | 0.4 |
| yk | ||||
| xk | -7.1 | 0.2 | 3.4 | 5.6 |
| yk | -4 | -2 | -2 | |
| xk | ||||
| yk | ||||
| xk | -5 | -4 | -2 | |
| yk | 0.2 | 0.25 | 0.23 | 0.19 |
| xk | 1.01 | 1.02 | 1.03 | 1.04 |
| yk | 2.7183 | 2.7732 | 2.8011 | 2.8292 |
| xk | 1.00 | 1.1 | 1.15 | 1.2 |
| yk | 0.3642 | 0.3329 | 0.3166 | 0.3012 |
| xk | 1.00 | 1.06 | 1.12 | 1.19 |
| yk | 1.17 | 1.27 | 1.36 | 1.49 |
| xk | 1.11 | 1.13 | 1.16 | 1.18 |
| yk | 3.03 | 3.09 | 3.18 | 3.25 |
| xk | 1.02 | 1.05 | 1.10 | 1.20 |
| yk | 0.5319 | 0.4976 | 0.4536 | 0.3624 |
| xk | 1.02 | 1.07 | 1.09 | 1.14 |
| yk | 1.56 | 1.62 | 1.69 | 1.72 |
| xk | 1.00 | 1.01 | 1.02 | 1.03 |
| yk | 0.01 | 0.0198 | 0.0296 | |
| xk | 1.04 | 1.05 | 1.06 | 1.07 |
| yk | 2.82 | 2.85 | 2.88 | 2.91 |
| xk | 1.10 | 1.11 | 1.12 | 1.13 |
| yk | 1.33 | 1.35 | 1.36 | 1.38 |
| xk | 1.15 | 1.16 | 1.17 | 1.18 |
| yk | 1.42 | 1.43 | 1.45 | 1.47 |
| xk | 1.08 | 1.09 | 1.1 | 1.11 |
| yk | 2.9447 | 2.9743 | 3.0042 | 3.0344 |
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: На стипендию можно купить что-нибудь, но не больше. 9016 — 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Лабораторная работа №2
Приближение функций, заданных таблично
Цель лабораторной работы
Приобретение практических навыков в построении интерполяционного многочлена Лагранжа и использование его для вычисления приближенных значений функций вне узлов интерполяции.
Приобретение практических навыков построения аппроксимирующих функций (аналитических зависимостей) по совокупности дискретных экспериментальных данных об изменениях значений функции при изменениях значений аргумента.
Задание
Для функций, заданных в таблице 1:
· построить интерполяционный многочлен Лагранжа и вычислить по нему значения функции для заданных значений аргумента;
· изучить технологию расчетов интерполяционных многочленов в Excel;
Для функций, заданных в таблице 2:
· Вычислить коэффициенты аппроксимирующих многочленов 1-й и 2-й степени, записать многочлены и построить их графики, на которые нанести также заданные табличные точки (расчеты выполнить в виде таблиц);
· изучить технологию регрессионного анализа с помощью Excel.
Интерполирование функций
Постановка задачи
Для функций, заданных таблицами их значений на конечном интервале, возникает необходимость вычисления значений функций для значений аргументов, отсутствующих в таблице. Тогда строят функцию, которая в заданных точках принимает заданные значения, а в остальных точках интервала приближенно представляет заданную функцию. А затем вычисления значений функции для любых значений аргумента в области определения заданной таблично функции выполняют по построенной функции. Задача интерполирования – построение такой приближенной функции. Чаще всего интерполирующую функцию отыскивают в виде алгебраического многочлена. Геометрически задача интерполирования заключается в построении кривой 
Интерполяционная формула Лагранжа
Пусть функция 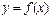




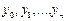
Интерполяционная формула Лагранжа в общем виде
где 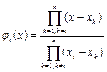
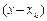


При этом в точках 
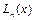
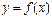



Пример 1.1. Запишем интерполяционный многочлен для функции, заданной тремя точками:
| X |
| Y |
Построить интерполяционный многочлен Лагранжа и вычислить приближенно значение функции для 
Для построения интерполяционного многочлена воспользуемся формулой при 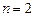

Интерполяционную формулу в Ехсеl можно построить достаточно простым способом. С практической точки зрения главная проблема заключается в вычислении в произвольной точке значений базисных функций.
Пример 1.2. Запишем интерполяционный многочлен для функции, заданной шестью точками:
| X0 | X1 | X2 | X3 | X4 | X5 | Y0 | Y1 | Y2 | Y3 | Y4 | Y5 | X |
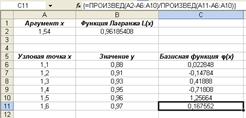
| 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 0,88 | 0,91 | 0,93 | 0,95 | 0,96 | 0,97 | 1,54 |
На рис. 1.1 представлены исходные данные, по которым будет выполняться интерполяция. На этом же рисунке проиллюстрирован процесс определения первой базисной функции.
В диапазоне ячеек А6:А11представлены заданные значения аргументов функции, а в диапазоне ячеек В6:В11– значения функции для узловых точек аргумента. В ячейку А2вводится значение аргумента, для которого необходимо вычислить значение интерполяционного полинома. Значение полинома будет выводиться в ячейке В2.Важным моментом является заполнение ячеек в диапазоне С6:С11,где будут отображаться значения базисных функций в точке, указанной в ячейке А2.Именно по этим значениям и значениям ячеек из диапазона А6:А11определяется значение интерполяционного полинома (ячейка В2).
Диапазон С6:С11заполняется так: отдельно первая и последняя ячейки диапазона, а все остальные ячейки — распространением одной формулы. В частности, в ячейку С6вводится формула
согласно которой определяется первая базисная функция. Сразу следует отметить, что и эта формула, и все прочие формулы из диапазона С6:С11,вводятся как формулы для диапазонов, т.е. с помощью нажатия комбинации клавиш Ctrl+Shift+Enter.Причина состоит в том, что аргументами функции ПРОИЗВЕД() указываются результаты арифметическихопераций с диапазонами.
Далее заполняются ячейки из диапазона С7:С10.Для этого в ячейку С7вводится формула
Абсолютные и относительные ссылки в формуле подобраны так, чтобы при ее копировании в следующие ячейки, ссылки на начальную А6 и конечную А11ячейки диапазона, равно как и на ячейку А2со значением переменной, для которой вычисляется базисная функция (и весь полином), оставались неизменными. Это абсолютные ссылки. Вместе с тем, в процессе копирования формулы произведения в ней вычисляются без учета значения аргумента в той строке, где размещена формула. После ввода формулы в ячейку С7данная формула с помощью маркера заполнения копируется во все ячейки, вплоть до С10 (Рис. 1.2).
Наконец, в ячейку С11необходимо ввести формулу
Поскольку формулы из начальной С6 и конечной С11ячеек диапазона С6:С11никуда копировать не предполагается, то и ссылки там относительные. Результат можно видеть на рис. 1.3.
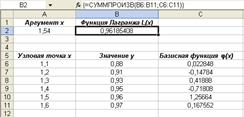
После этого осталось только вычислить интерполяционный полином. Для этого достаточно в ячейку В2ввести формулу
Эта формула вводится как обычная, то есть нужно нажать клавишу Enter.Результат представлен на рис. 1.4.
Чтобы посчитать значение полинома в какой-то точке, соответствующее значение следует ввести в ячейку А2. В ячейке В2практически сразу появится результат.
Ответ:
На рис. 1.5 проиллюстрирована ситуация, когда в качестве аргумента указано узловое значение. Как и следовало ожидать, в узловой точке значение интерполяционного полинома равно табличному значению функции в этой точке, а все базисные функции, кроме той, что соответствует указанному узлу, равны нулю. Отличная от нуля базисная функция равна единице.