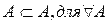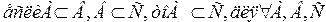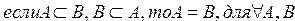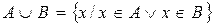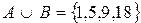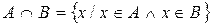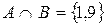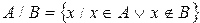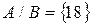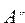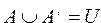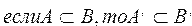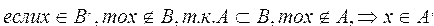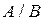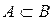Задачи по математике для 3 класса.
Задача 1
Задай свойством множества А и В:
Каждый ли заяц является животным? Всякое ли животное является зайцем? Какое из этих множеств является частью другого?
Решение:
- B — животные
- A — зайцы
- Каждый заяц является животным
- Не каждое животное является зайцем
- Зайцы являются частью множества животные
Задача 2
Задай свойством множества, изображённые на рисунке. Какое из них является подмножеством другого? Сделай записи.
Как расположены относительно друг друга диаграммы множества и подмножества?
Решение:
- а) M множество — грибы; C подмножество грибов — съедобные грибы, поэтому — C ⊂ M
- б) D множество — деревья; B подмножество хвойные деревья, поэтому — B ⊂ D
- в) P множество прямоугольники; K подмножество квадраты, поэтому — K ⊂ P
- г) E множество прямоугольники; F множество геометрические фигуры. F ⊄ E потому что не все геометрические фигуры — прямоугольники.
- Диаграмма подмножества находится внутри диаграммы множества
Задача 3
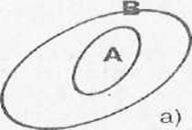
Определи по рисунку, какое из множеств является подмножеством другого:
Задача 4
Нарисуй диаграммы множеств. Запиши, какое из них является подмножеством другого.
- а) С — множество учеников школы, В — множество отличников этой школы.
- б) D — множество девочек класса, Е — множество всех учеников этого класса.
- в) К — множество рыб, О — множество окуней.
- г) N — множество натуральных чисел, М — множество чётных чисел.
Задача 5
- а) Какое из множеств М = <а; b;
;
; +> и К =
> является подмножеством другого множества? Докажи.
- б) Нарисуй диаграмму Венна множеств М и К и отметь на ней элементы этих множеств.
Решение:
- а) K ⊂ M. M — множество фигур, букв и знаков, b — пиринадлежит множеству букв,
— принадлежит множеству фигур.
Задача 6
Составь задачу по картинке и реши ее:
В магазине было 5 яблок и 2 груши стоимостью 36 рублей, из них было продано 2 яблока и 2 груши за 24 рубля. Сколько стоит 1 яблоко и 1 груша.
- 36 – 24 =12 рублей стоит 3 яблока
- 12 : 3 = 4 рубля стоит 1 яблоко
- 4 * 2 = 8 рублей стоит 2 яблока
- 24 – 8 = 16 рублей стоят 2 груши
- 16 : 2 = 8 рублей стоит 1 груша
Задача 7
- Составь выражение и найди его значение.
- а) На одной улице 18 одноэтажных домов и 3 двухэтажных. Во сколько раз одноэтажных домов больше, чем двухэтажных?
- б) В одном доме 10 квартир. Это в 5 раз меньше, чем в другом. Сколько квартир в двух домах?
- в) На каждом этаже 7-этажного дома по 6 квартир, а на каждом этаже 9-этажного дома по 4 квартиры. В каком доме больше квартир и на сколько?
- г) В одном доме 56 квартир, а в другом — в 7 раз меньше. На сколько квартир в первом доме больше, чем во втором?
Задача 8
- 91 : 7 = 13
- 80 : 5 = 16
- 64 : 4 = 16
- 78 : 3 = 26
- (39 + 29) : 4 = 68 : 4 = 17
- (60-5) : 5 = 55 : 5 = 11
- 63 : (3 * 7) = 63 : 21 = 3
- 240 : (80 : 2) = 240 : 40 = 6
- 19 + 17 * 3 — 46 = 19 + 51 — 46 = 70 — 46 = 24
- 54 — 26 + 38 — 3 =28 +38 — 3 = 66 — 3 = 63
- 48 : 2 + 60 : 2 = 24 + 30 = 54
- (19 * 5 — 5): 30 = 90 : 30 = 3
Задача 9
а) Отметь на числовом луче двузначные числа, кратные 12:
Решение:
б) Выполни деление с остатком:
Решение:
- 37 : 12 = 6 (ост. 1)
- 50 : 12 = 4 (ост. 2)
- 68 : 12 = 5 (ост. 8)
- 75 : 12 = 6 (ост. 3)
- 99 : 12 = 8 (ост. 3)
Множество – совокупность любых объектов. Множества обозначают большими буквами латинского алфавита – от A до Z.
Основные числовые множества: множество натуральных чисел и множество целых чисел, всегда обозначаются одними и теми же буквами:
N – множество натуральных чисел
Z – множество целых чисел
Элемент множества – это любой объект, входящий в состав множества. Принадлежность объекта к множеству обозначается с помощью знака ∈ . Запись
читается так: 5 принадлежит множеству Z или 5 – элемент множества Z .
Множества делятся на конечные и бесконечные. Конечное множество – множество, содержащее определённое (конечное) количество элементов. Бесконечное множество – множество, содержащее бесконечно много элементов. К бесконечным множествам можно отнести множества натуральных и целых чисел.
Для определения множества используются фигурные скобки, в которых через запятую перечисляются элементы. Например, запись
означает, что множество L состоит из четырёх чётных чисел.
Термин множество употребляется независимо от того, сколько элементов оно содержит. Множества не содержащие ни одного элемента называются пустыми.
Подмножество
Подмножество – это множество, все элементы которого, являются частью другого множества.
Визуально продемонстрировать отношение множества и входящего в него подмножества можно с помощью кругов Эйлера. Круги Эйлера – это геометрические схемы, помогающие визуализировать отношения различных объектов, в нашем случае, множеств.
Рассмотрим два множества:
Каждый элемент множества L принадлежит и множеству M, значит, множество L является подмножеством множества M. Такое соотношение множеств обозначают знаком ⊂ :
Запись L⊂M читается так: множество L является подмножеством множества M .
Множества, состоящие из одних и тех же элементов, независимо от их порядка, называются равными и обозначаются знаком = .
Рассмотрим два множества:
Так как оба множества состоят из одних и тех же элементов, то L = M.
Пересечение и объединение множеств
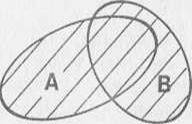
Пересечение двух множеств – это совокупность элементов, принадлежащих каждому из этих множеств, то есть их общая часть. Пересечение обозначается знаком ∩ .
Запись L∩M читается так: пересечение множеств L и M .
Из данного примера следует, что пересечением множеств называется множество, которое содержит только те элементы, которые встречаются во всех пересекающихся множествах.
Объединением двух множеств называется множество, содержащее все элементы исходных множеств в единственном экземпляре, то есть если один и тот же элемент встречается в обоих множествах, то в новое множество этот элемент будет включён только один раз. Объединение обозначается знаком ∪ .
Запись L∪M читается так: объединение множеств L и M .
При объединении равных множеств объединение будет равно любому из данных множеств:
Понятие множества – одно из основных понятий математики. Под множеством понимают совокупность объектов (предметов или понятий), которая рассматривается как единое целое. Например, можно говорить о множестве натуральных чисел, о множестве букв на данной странице, о множестве корней данного уравнения и т. п. Понятие множества принимается как исходное, первичное, т. е. несводимое к другим понятиям. Объекты, входящие в состав множества, называются его элементами. Обычно множества обозначаются большими печатными буквами английского алфавита, например, множество А; а его элементы маленькими прописными буквами, например, элемент а.
Запись 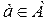
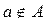
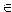
Определение 1. Два множества А и В называются равными и пишут А=В, если множества А и В содержат одни и те же элементы.
Например: <2, 4, 6>= <4, 2, 6>– равные множества.
Определение 2. Множество называется непустым, если содержит хотя бы один элемент.
Определение 3. Множество А является подмножеством множества В, если каждый элемент множества А принадлежит множеству В.
В этом случае пишут 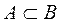
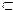
Например: <2, 4,>
Рассмотрим свойства отношения включения.
рефлексивно, т.е любое множество является подмножеством самому себе.
транзитивно, т. е. для любых множеств А, В и С, если множество А является подмножеством множества В и множество В является подмножеством множества С, то из этого следует, что множество А является подмножеством множества С.
антисимметрично, т. е. для любых множеств А и В следует, что, если множество А является подмножеством множества В и в то же время множество В является подмножеством множества А, то множества А и В равны.
Определение 4. Множество, не содержащее ни одного элемента, называется пустыммножеством.

Пустое множество является подмножеством любого множества.
Определение 5. Множество всех подмножеств множества A называется множеством-степенью и обозначается P(A).
В дальнейшем будем пользоваться следующим утверждением:
Утверждение 1. Число всех подмножеств конечного множества равно 2n.
Пример. Выделим все подмножества множества А =<2, 4, 6>.
Р(А)=<2, 4, 6>, <2, 4>, <4, 6>, <2, 6>, <2>, <4 >, <6>, 
Операции над множествами
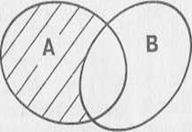
Объединением множеств А и В называется множество, состоящее из тех элементов, которые принадлежат одному из множеств А или В.
Для обозначения объединения множеств используют знак 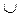
Пример. 

Пересечением множеств А и В называются такое множество, элементы которого принадлежат как множеству А, так и множеству В.
Для обозначения пересечения множеств используют знак 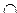
Пример. 

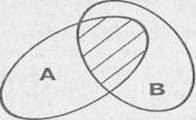
Разностью множеств А и В называется множество, элементы которого являются элементами множества А, не принадлежащие множеству В.
Для обозначения разности множеств используют знак /.
Пример. 

Перечислим основные свойства операций над множествами:
1) 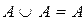
2) 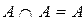
3) 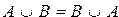
4) 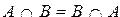
5) 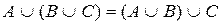
6) 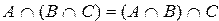
7) 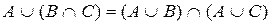
8) 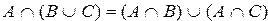
Универсальное множество. Дополнение множества.
Во многих приложениях теории множеств рассматриваются только такие множества, которые содержатся в некотором фиксированном множестве. Например, в геометрии мы имеем дело с множеством точек данного пространства, в арифметике – с множеством целых чисел. Такое фиксированное множество называют универсальным.Для его обозначения используют букву U.
Определение 6. Множество U/А называется дополнением множества А и обозначается 

Дополнение U/ 

Справедливы следующие формулы:
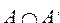
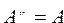
Теорема. Если множество А является подмножеством множества В, то дополнение множества А будет являться подмножеством дополнения множества В.
Пусть множество А является подмножеством множества В, 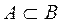
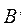

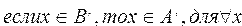
Действительно, если х принадлежит множеству 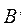

Теорема. Имеют место следующие тождества
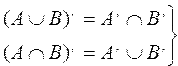
Приведем краткое доказательство первого утверждения.
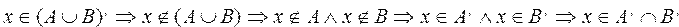
Для графического изображения множеств и их свойств используются так называемые диаграммы Эйлера-Венна.
Объединение множеств Пересечение множеств
Разность множеств Подмножество
Универсальное множество Дополнение
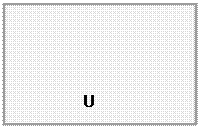 | 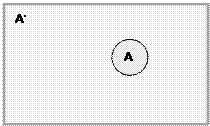 |






 ;
;  ; +> и К =
; +> и К =