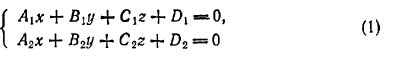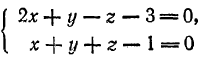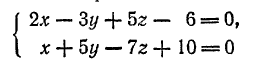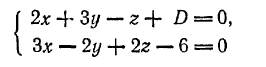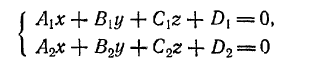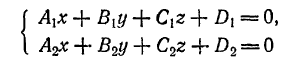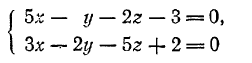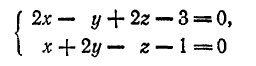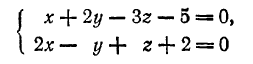Прямая как пересечение двух плоскостей определяется совместным заданием двух уравнений первой степени:

при условии, что коэффициенты A1, В1, С1 первого из них не пропорциональны коэффициентам А2, В2, С2 второго (в противном случае эти уравнения будут определять параллельные или слившиеся плоскости).

Пусть некоторая прямая а определена уравнениями (1) и α и β — какие угодно числа, одновременно не равные нулю; тогда уравнение

определяет плоскость, проходящую через прямую а.

Уравнением вида (2) (при соответствующем выборе чисел α, β можно определить любую плоскость, проходящую через прямую а.

Совокупность всех плоскостей, проходящих через одну и ту же прямую, называется пучком плоскостей. Уравнение вида (2) называется уравнением пучка плоскостей.

Если α ≠ 0, то, полагая β/α = λ, уравнение (2) можно привести к виду

В таком виде уравнение пучка плоскостей более употребительно, чем уравнение (2). однако уравнением (3) можно определить все плоскости пучка, за исключением той, которой соответствует а = 0, т. е. за исключением плоскости A2х + В2у + C2z + D2 = 0.

982. Составить уравнения прямых, образованных пересечением плоскости 5x — 7y + 2z — 3 = 0 с координатными плоскостями.

983. Составить уравнения прямой, образованной пересечением плоскости 3x — y — 7z + 9 = 0 с плоскостью, проходящей через ось Ох и точки E(3; 2; -5).

984. Найти точки пересечения прямой

с координатными плоскостями.

985. Доказать, что прямая

пересекает ось Оу.

986. Определить, при каком значении D прямая

пересекает: 1) ось Ох; 2) ось Оу; 3) ось Oz.

987. Найти соотношения, которым должны удовлетворять коэффициенты уравнений прямой

для того, чтобы эта прямая была параллельна: 1) оси Ох; 2) оси Оу; 3) оси Oz.

988. Найти соотношения, которым должны удовле-творять коэффициенты уравнений прямой

для того, чтобы эта прямая пересекала: 1) ось абсцисс;2) ось ординат; 3) ось апликат; 4) совпадала с осью абсцисс; 5) совпадала с осью ординат; 6) совпадала с осью апликат.

989. В пучке плоскостей 2x — 3y + z — 3 + λ(x + 3y + 2z + 1) = 0 найти плоскость, которая: 1) проходит через точку М,(1; -2;3); 2) параллельна оси Ох; 3) параллельна оси Оу; 4) параллельна оси Oz.

990. Составить уравнение плоскости, которад про-ходит через прямую пересечения плоскостей Зх — у + 2z + 9 = 0, х + z — 3 = 0: 1) и через точку М1 (4; -2; -3); 2) параллельно оси Ох; 3) параллельно оси Оу; 4) параллельно оси Oz.

991. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей 2х — у + 3z — 5 = 0, х + 2у — z + 2 = 0 параллельно вектору l = <2; — 1; -2>.

992. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей 5х — 2y — z — 3 = 0, х + Зу — 2z + 5 = 0 параллельно вектору l = <7; 9; 17>.

993. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей Зх — 2у + z — З = 0, х — 2z = 0 перпендикулярно плоскости х — 2y + 2 + 5 = 0.

994. Составить уравнение плоскости, проходящей через прямую

перпендикулярно плоскости х + 19y — 7z — 11 = 0.

995. Составить уравнение плоскости, которая прохо-дит через прямую пересечения плоскостей 2х + y — z + 1 = 0, х + y + 2z + 1 = 0 параллельно отрезку, ограниченному точками M1(2; 5; -3) и М2(3; -2; 2).

996. Написать уравнение плоскости, принадлежащей пучку плоскостей α(Зх — 4y + z + 6) + β (2х — 3y + z + 2) = 0 и равноудаленной от точек М1(З; -4; -6), М2(1; 2; 2).

997. Определить, принадлежит ли плоскость 4х — 8y + 17z — 8 = 0 пучку плоскостей α (5х — у + 4z — 1) + β (2х + 2у — 3z + 2) = 0.

998. Определить, принадлежит ли плоскость 5х — 9у — 2z + 12 = 0 пучку плоскостей α(2х — 3у + z — 5) + β(х — 2у — z — 7) = 0.

999. Определить, при каких значениях l и m плоскость 5х + lу + 4z + m = 0 принадлежит пучку плоскостей α (Зх — 7у + z — 3) + β(х — 9y — 2z + 5) = 0.

1000. Написать уравнение плоскости, которая при-надлежит пучку плоскостей α (х — Зу + 7z + 36) + β(2х + у — z — 15) = 0 и отстоит от начала координат на расстоянии р = 3.

1001. Написать уравнение плоскости, которая при-надлежит пучку плоскостей α(10х — 8у — 15z + 56) + β (4х + y + 3z — 1) = 0 и отстоит от точки С (3; -2; -3) на расстоянии d = 7.

1002. Найти уравнение плоскости, которая принадлежит пучку плоскостей α(4x + 13у — 2z — 60) + β (4x + 3у + 3z — 30) = 0 и отсекает от координатного угла Оху треугольник с площадью, равной 6 кв. ед.

1003. Составить уравнения плоскостей, проектирующих прямую

на координатные плоскости.

1004. Составить уравнения проекций прямой

на координатные плоскости.

1005. Составить уравнение плоскости, проектирующей прямую

Свойства прямой в евклидовой геометрии.

Через любую точку можно провести бесконечно много прямых.

Через любые две несовпадающие точки можно провести единственную прямую.

Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются

параллельными (следует из предыдущего).

В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:

  • прямые пересекаются;
  • прямые параллельны;
  • прямые скрещиваются.

Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия

задается на плоскости уравнением первой степени (линейное уравнение).

Общее уравнение прямой.

Определение. Любая прямая на плоскости может быть задана уравнением первого порядка

причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим

уравнением прямой. В зависимости от значений постоянных А, В и С возможны следующие частные случаи:

• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат

• А = 0, В ≠0, С ≠0 — прямая параллельна оси Ох

• В = 0, А ≠0, С ≠ 0 – прямая параллельна оси Оу

• В = С = 0, А ≠0 – прямая совпадает с осью Оу

• А = С = 0, В ≠0 – прямая совпадает с осью Ох

Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных

Уравнение прямой по точке и вектору нормали.

Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В)

перпендикулярен прямой , заданной уравнением

Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору (3, -1).

Решение. Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С

подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно

С = -1. Итого: искомое уравнение: 3х – у – 1 = 0.

Уравнение прямой, проходящей через две точки.

Пусть в пространстве заданы две точки M 1 ( x 1 , y 1 , z 1 ) и M2 ( x 2, y 2 , z 2 ), тогда уравнение прямой,

проходящей через эти точки:

Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На

плоскости записанное выше уравнение прямой упрощается:

Дробь = k называется угловым коэффициентом прямой.

Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).

Решение. Применяя записанную выше формулу, получаем:

Уравнение прямой по точке и угловому коэффициенту.

Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:

и обозначить , то полученное уравнение называется

уравнением прямой с угловым коэффициентом k.

Уравнение прямой по точке и направляющему вектору.

По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание

прямой через точку и направляющий вектор прямой.

Определение. Каждый ненулевой вектор (α1, α2), компоненты которого удовлетворяют условию

Аα1 + Вα2 = 0 называется направляющим вектором прямой.

Пример. Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).

Решение. Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением,

коэффициенты должны удовлетворять условиям:

1 * A + (-1) * B = 0, т.е. А = В.

Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0.

при х = 1, у = 2 получаем С/ A = -3, т.е. искомое уравнение:

Уравнение прямой в отрезках.

Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим:

или , где

Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения

прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.

Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.

С = 1, , а = -1, b = 1.

Нормальное уравнение прямой.

Если обе части уравнения Ах + Ву + С = 0 разделить на число , которое называется

нормирующем множителем, то получим

xcosφ + ysinφ — p = 0 – нормальное уравнение прямой.

Цель:Ввести общее понятие уравнение прямой линии. Изучить понятие угла наклона прямой, углового коэффициента прямой. Дать различные виды уравнения прямой, уметь по условию задачи выбрать наиболее подходящее уравнение для рационального решения задачи. Рассмотреть угол между двумя прямыми и условия параллельности и перпендикулярности двух прямых.

Ключевые слова:уравнение линии, общее уравнение прямой, уравнение прямой с угловым коэффициентом, уравнение пучка прямых, уравнение прямой, проходящей через две данные точки, уравнение в отрезках, угол между прямыми.

План лекции

1. Уравнение прямой линии на плоскости.

2. Различные уравнения прямой на плоскости.

3. Угол между двумя прямыми.

4. Условия параллельности и перпендикулярности прямых.

5. Расстояние от точки до данной прямой.

1. Уравнение прямой линии на плоскости.

Аналитической геометрией называется раздел математики, в котором геометрические задачи решаются алгебраическим путем. Основой аналитической геометрии является метод координат, впервые использованный Декартом. Сущность его в том, что положение точки рассматривается относительно некоторых линий, образующих систему координат на плоскости или в пространстве.

Уравнением линии на плоскости ХОУ называется уравнение, которому удовлетворяют координаты х и у каждой точки этой линии и не удовлетворяют координаты любой точки не лежащей на этой линии. Если точка М (х; у) передвигается по линии L, то ее координаты х и у, изменяясь, все время удовлетворяют уравнению этой линии. Поэтому координаты точки М называются текущими координатами точки данной линии.

2. Различные уравнения прямой на плоскости

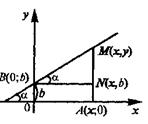
Пусть прямая пересекает ось Оу в точке В (0,b) и образует с осью Ох угол (0

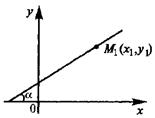
Уравнение прямой, проходящей через данную точку в данном направлении.

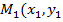
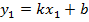
Пусть прямая проходит через точку ) и образует с осью Ох угол (рис.3). Так как точка ) лежит на прямой, то ее координаты удовлетворяют уравнению (2), т.е.

(3)

Вычитая равенство (3) из равенства (2), получим уравнение искомой прямой

(4)

Уравнение пучка прямых.

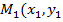
Если в уравнении (4) — произвольное число, то это уравнение определяет пучок прямых, проходящих через точку ), кроме прямой, параллельной оси
Оу и не имеющей углового коэффициента (рис. 4).

Уравнение прямой, проходящей через две данные точки.

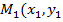
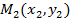
Пусть даны две точки ), и , .

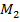
Для составления уравнения прямой (Рис. 5) запишем уравнение пучка прямых, проходящих через точку :

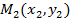
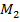
Так как точка лежит на данной прямой, то чтобы выделить ее из пучка, подставим координаты точки в уравнение пучка

и найдем угловой коэффициент прямой

(5)

Теперь уравнение искомой прямой примет вид

или (6)

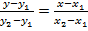
Уравнение прямой в отрезках

Найдем уравнение прямой по заданным отрезкам и , отсекаемым на осях координат. Используя (6), уравнение прямой, проходящей через точки и (рис. 6), примет вид

или после преобразований . (7)

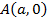
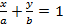
Уравнение (7) называется уравнением прямой в отрезках.

Общее уравнение прямой.

Рассмотрим уравнение первой степени с двумя переменными в обшем виде

, (8)

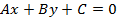
в котором коэффициенты А и В не равны одновременно нулю, т.е.

1. Пусть . Тогда уравнение (8) можно записать

.

Обозначим , .

Если , то получим (уравнение прямой с угловым коэффициентом); если , то (уравнение прямой, проходящей через начало координат); если , то (уравнение прямой, параллельной оси OY), если , то (уравнение оси OX).

2. Пусть . Тогда уравнение (8) примет вид

Обозначим . Если , то получим (уравнение прямой, параллельной оси OY), если , то (уравнение оси OY).

Таким образом, при любых значениях коэффициентов А, В (не равных одновременно нулю) и С уравнение (8) есть уравнение некоторой прямой линии па плоскости Оху.

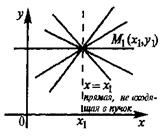
Уравнение (8) называется общим уравнением прямой. Заметим, что в отличие от уравнения пучка прямых (4) общее уравнение (8) включает и уравнение любой вертикальной прямой, параллельной оси Оу.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8451 — | 7340 — или читать все.