Инструменты пользователя

Инструменты сайта

Содержание

Площадь прямоугольника

Площадь прямоугольника равна произведению его смежных сторон.

Доказательство

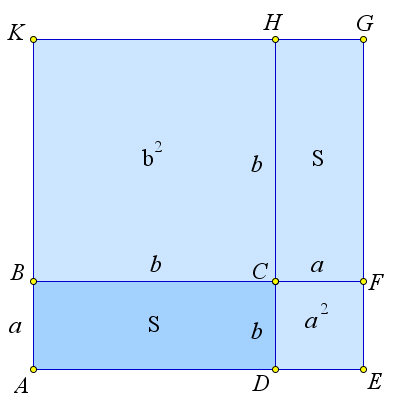
Рассмотрим прямоугольник $ABCD$ со сторонами $AB=a$ и $BC=b$.

Докажем, что его площадь $S=ab$.

Достроим прямоугольник $ABCD$ до квадрата $AEGK$, продлив прямую $AD$ за точку $D$ на отрезок $DE=a$, и прямую $AB$ за точку $B$ на отрезок $BK=b$.

Тогда $BCHK$ и $CFED$ – это квадраты, и их площади равны соответственно $b^2$ и $a^2$.

Кроме того, $CFGH$ – это прямоугольник со сторонами $a$ и $b$, следовательно, его площадь равна площади $ABCD$.

Обозначим площадь $ABCD$ за $S$.

С другой стороны $S_=(a+b)^2=a^2+b^2+2ab$.

Откуда получаем, что $2ab=2S$, то есть $S=ab$.

Площадь прямоугольного треугольника

Площадь прямоугольного треугольника равна полупроизведению его катетов.

Доказательство

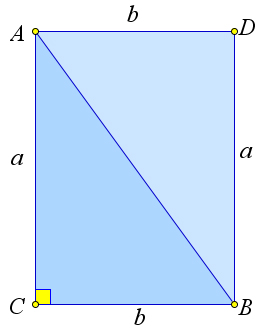
Рассмотрим прямоугольный треугольник $ riangle ABC$, в котором $BC=a, AC=b$ и $a C=90^circ$.

Достроим треугольник $ riangle ABC$ до прямоугольника $ADBC$.

Площадь треугольника

Площадь треугольника равна половине произведения любой из его сторон и проведенной к ней высоты.

Доказательство

Рассмотрим треугольник $ABC$, в котором $BH$ – это высота.

Докажем, что $S_=dfrac<1><2>cdot BHcdot AC.$

Возможны три случая:

Первый случай

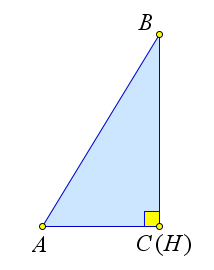
Пусть высота из точки $B$ падает в один из концов отрезка $AC$, например в вершину $C$.

Тогда $BC=BH$ и $ riangle ABC$ – прямоугольный, следовательно, по теореме получаем $S_=dfrac<1><2>cdot BHcdot AC$.

Второй случай

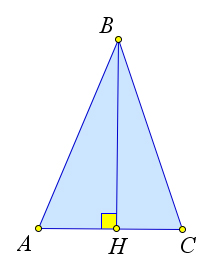
Пусть высота $BH$ падает внутрь отрезка $AC$.

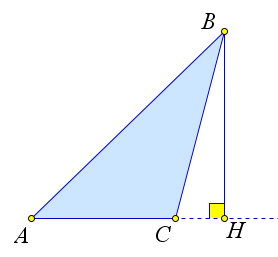
Тогда высота $BH$ разбивает треугольник $ABC$ на два прямоугольных треугольника $ABH$ и $BHC$, следовательно, $S_=S_+S_=dfrac<1><2>cdot BHcdot AH+dfrac<1><2>cdot BHcdot HC=dfrac<1><2>cdot BHcdot (AH+HC)=frac<1><2>cdot BHcdot AC$.

Третий случай

Пусть высота $BH$ падает вне отрезка $AC$, например за точку $C$.

$S_=S_-S_=dfrac<1><2>cdot BHcdot AH-dfrac<1><2>cdot BHcdot CH=dfrac<1><2>cdot BHcdot (AH-CH)=dfrac<1><2>cdot BHcdot AC$.

Площадь параллелограмма

Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.

Доказательство

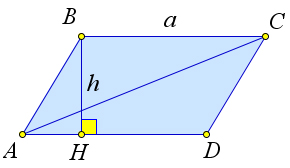
Рассмотрим параллелограмм $ABCD$, в котором сторона $AD=a$ и высота $BH=h$.

Докажем, что $S_=ah$.

Проведем диагональ $AC$.

По свойствам параллелограмма, диагональ делит его на два равных треугольника.

Площадь трапеции

Площадь трапеции равна произведению высоты на полусумму ее оснований.

Доказательство

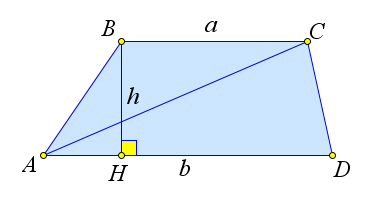
Рассмотрим трапецию $ABCD$, в которой $BH=h$ – высота, и основания $AD=a, BC=b$.

Проведем диагональ $AC$.

Тогда $S_< riangle ABD>=dfrac<1><2>cdot ah$, $S_< riangle BCD>=dfrac<1> <2>ah$, поскольку высоты этих треугольников, проведенные к сторонам $AD$ и $BC$ соответственно, равны высоте трапеции.

Площадь ромба

Площадь ромба равна полупроизведению его диагоналей.

Доказательство

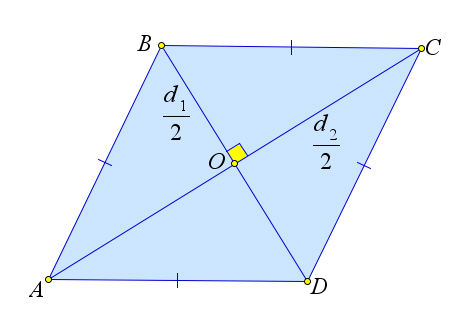
Рассмотрим ромб $ABCD$, в котором диагонали $AC=d_1$ и $BD=d_2$.

Докажем, что $S_=dfrac<1><2>cdot d_1d_2$.

Пусть диагонали $AC$ и $BD$ пересекаются в точке $O$.

Диагонали разбивают ромб на четыре равных треугольника $ riangle ABO, riangle BCO, riangle CDO, riangle DAO$.

Теорема (о площади четырехугольника с перпендикулярными диагоналями)

Площадь выпуклого четырехугольника со взаимно перпендикулярными диагоналями равна полупроизведению его диагоналей.

Доказательство

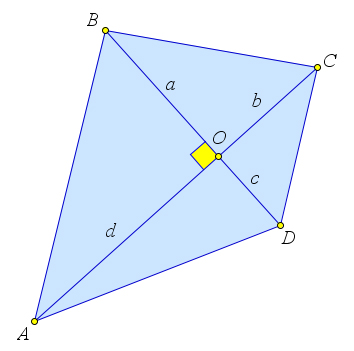
Рассмотрим четырехугольник $ABCD$ в котором $ACperp BD$.

Пусть $AC$ пересекает $BD$ в точке $O$.

Обозначим $BO=a, CO=b, DO=c, AO=d$.

Теорема (о площадях боковых треугольников в трапеции)

Два треугольника, образованные боковыми сторонами трапеции и отрезками ее диагоналей, равны по площади.

Доказательство

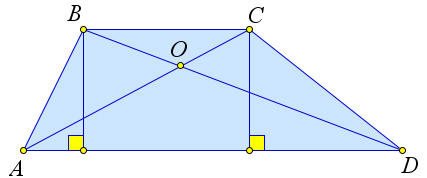
Рассмотрим трапецию $ABCD$, у которой диагонали $AC$ и $BD$ пересекаются в точке $O$.

Рассмотрим треугольники $ riangle ABD$ и $ riangle ACD$.

У этих треугольников общее основание $AD$, кроме того их высоты, проведенные к стороне $AD$ из точек $B$ и $C$ соответственно, тоже равны.

Ответ

Пошаговое объяснение:

Для доказательства делаем рисунок — в приложении.

Фигура ABCD — прямоугольник — стороны равны и перпендикулярны.

Площадь прямоугольника по формуле: S(ABCD) = a*b.

Треугольники ABC ADC — равны — по двум сторонам и углу в 90 град.

S(ABC) = S(ADC) = 1/2*S(ABCD) = a*b/2 — площадь треугольника — ответ.

8 класс. Геометрия. Площадь. Площадь треугольника и трапеции.

  • Оглавление
  • Занятия
  • Обсуждение
  • О курсе

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

Формула для площади треугольника и следствия из неё

На данном уроке мы докажем формулу для площади треугольника и решим несколько задач на её применение.

Будем называть сторону – основанием, тогда – высота, опущенная к этой стороне (см. Рис. 1).

Рис. 1. Высота и основание

Теорема о свойстве медианы треугольника

Площадь треугольника равна половине произведения его основания на высоту.

В формульном виде: .

Доказательство:

Рис. 2. Иллюстрация к теореме

Достроим треугольник до параллелограмма – см. Рис. 2.

(по трём сторонам: – общая, , – как противоположные стороны параллелограмма).

Из равенства треугольников следует равенство их площадей: . Получаем: . Воспользовавшись формулой для площади параллелограмма: .

Сформулируем несколько следствий из данной теоремы.

Следствие 1

Площадь прямоугольного треугольника равна половине произведения его катетов (см. Рис. 3).

Рис. 3. Иллюстрация к следствию 1

.

Следствие 2

Если высоты двух треугольников равны, то их площади относятся как основания (см. Рис. 4).

Рис. 4. Иллюстрация к следствию 2

.

Теорема 2

Медиана треугольника разбивает его на два равновеликих треугольника (см. Рис. 5).

Доказательство:

Рис. 5. Иллюстрация к теореме

Пусть – треугольник, – медиана, – высота. Для треугольников – также является высотой. Запишем формулу для площади каждого из этих треугольников: , . Так как ( – медиана), то: . Значит, эти треугольники являются равновеликими.

Формула для площади ромба

Теорема 3

Площадь ромба равна половине произведения его диагоналей (см. Рис. 6).

В виде формулы: .

Доказательство:

Рис. 6. Иллюстрация к теореме

(по 3 сторонам: – общая, – свойства ромба). Из равенства треугольников следует равенство их площадей. Значит: . Но формулу для площади треугольника мы уже знаем: (т. к. , поэтому – высота треугольника ). Получаем следующее равенство: ( – свойство диагоналей ромба).

Свойство треугольников с равными углами

Теорема 4

Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

В виде формулы: .

Доказательство:

Рис. 7. Иллюстрация к теореме

Совместим треугольники так, чтобы вершина совпала с вершиной , сторона лежала на прямой , а сторона лежала на прямой .

Рис. 8. Иллюстрация к теореме

Рассмотрим отношение площадей треугольников и . Эти треугольники имеют общую высоту, проведённую из вершины , поэтому, по следствию 2 из теоремы 1, их площади относятся как основания, то есть: .

Из аналогичных соображений: . Перемножив эти два равенства, получим: .

Задачи на площадь треугольника и следствия из неё

Теперь решим несколько задач, используя доказанные формулы и свойства.

Задача 1

Площадь прямоугольного треугольника равна . Найдите катеты этого треугольника, если известно, что один из них составляет другого.

Решение

Пусть один из катетов равен , а второй – . Тогда площадь треугольника можно вычислить по формуле: . Но, по условию: . Подставив это выражение, получаем: . Откуда: .

Ответ: .

Задача 2

В треугольнике точка лежит на стороне , точка лежит на стороне . Кроме того: , , . Чему равна площадь треугольника (Рис. 9)?

Решение:

Рис. 9. Иллюстрация к задаче

Воспользуемся теоремой 4 для треугольников и ( – общий угол этих треугольников). Из этой теоремы следует, что: . Значит: .

Ответ: .

На этом уроке мы рассмотрели понятия площадей треугольника и ромба, вывели из них некоторые следствия. На следующем уроке мы научимся вычислять площадь трапеции.