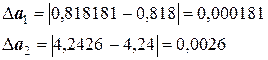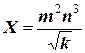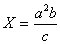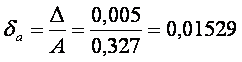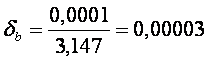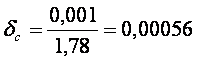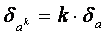Изучаемые вопросы: Источники и классификация погрешности. Запись чисел в ЭВМ. Абсолютная и относительная погрешности. Формы записи данных. О вычислительной погрешности. Погрешности функций.
После изучения этой темы Вам следует ответить на вопросы для самопроверки.
Следует различать погрешности измерений и погрешности решения задач. Первые изучаются в физике, а вторые обуславливаются несколькими причинами: неточностью модели, описывающей то или иное явление, неточностью метода решения и неточностью данных на этапе ввода их для решения, или вывода результатов округления. Поэтому говорят о неустранимых погрешностях, погрешностях метода и вычислительных погрешностях.
Если 




Относительной погрешностью приближённого значения 


Часто её выражают в процентах.
Абсолютную и относительную погрешности принято записывать в виде числа, содержащего одну или две значащие цифры в форме

Пример 1. ○Абсолютная и относительная погрешности числа 
Число 




Значащими цифрами числа 
Пример 2. ○Подчёркнуты значащие цифры в следующих числах:
Значащая цифра числа 
Пример 3. ○Верные цифры числа 
Если 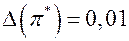

если 

если 

Для оценки погрешности арифметических действий используют следующие правила.
Абсолютные погрешности суммы или разности не превосходят абсолютной погрешности их членов:

Относительные погрешности в этом случае

Абсолютные погрешности произведения и частного рассчитывают по формулам
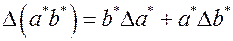
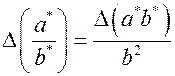
соответственно. Их относительные погрешности равны:


Пример 4. Вычислить и определить погрешности результата.
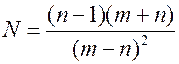

○Имеем
Тогда абсолютная погрешность равна 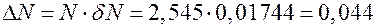
Итак, 
Существенную часть теории численных методов составляет построение устойчивых алгоритмов, использование которых ведёт к искажению результатов вычислений с погрешностью, находящейся в заданных пределах. В этом случае говорят о вычислительной погрешности. Например, потеря значащих цифр происходит при вычитании близких больших чисел. Если такие числа округлить с большой абсолютной погрешностью, то результат вычитания их также даст большую абсолютную погрешность. Во избежание этого такие расчёты следует проводить с двойной точностью.
Следует помнить, что предельная абсолютная погрешность суммы или разности равна сумме предельных погрешностей, а предельная относительная погрешность произведения или частного равна сумме предельных относительных погрешностей.
Подробнее об этой теме можно узнать из [7], c.17-34.
Вопросы для самопроверки по теме 1.1
1. Что такое абсолютная и относительная погрешности?
2. Можно ли выражать погрешность в процентах? Какую погрешность?
3. В какой форме записывают абсолютную и относительную погрешности?
4. Чему равны погрешности суммы и разности, а также произведения и частного? О каких погрешностях в данных случаях идёт речь?
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8829 — 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
В практике вычислений, производимых с приближенными числами, неизбежно возникает вопрос о влиянии погрешностей исходных чисел на погрешность конечного результата. Рассмотрим эту проблему подробнее.
Предположим, что вычисляется сумма С приближенных чисел Аi , т.е.
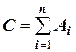
где 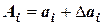
Искомую сумму можно записать так:
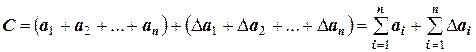
или 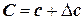
где 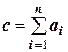
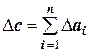
Правило 6: при сложении (вычитании) приближенных чисел результат является также приближенным числом, у которого абсолютная погрешность равна сумме абсолютных погрешностей всех слагаемых.
Относительная погрешность суммы рассчитывается следующим образом:

Следует обратить внимание на то, что погрешность каждого слагаемого имеет знак (±), тем не менее при вычислении суммы (или разности приближенных чисел) погрешности слагаемых всегда записываются со знаком (+), но погрешность суммы ∆с будет иметь знак (±).
Определим правило расчета погрешности произведения приближенных чисел. Для этого рассмотрим частную задачу – найдем произведение двух приближенных чисел
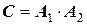
где 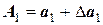
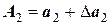
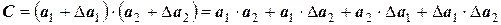
Так как из всех слагаемых последнее парное произведение является бесконечно малой величиной более высокого порядка, им можно пренебречь. Тогда, разделив вышеприведенное равенство на произведение 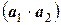
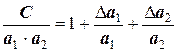
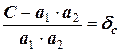
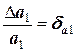
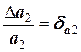
получаем значение относительной погрешности произведения
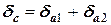
значение абсолютной погрешности произведения
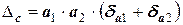
Эти выводы можно распространить на любое количество сомножителей. Действительно, если находится произведение приближенных чисел
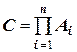
где 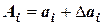
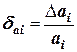
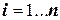
то 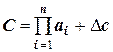
где 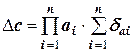
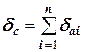
Правило 7. При умножении приближенных чисел результат будет иметь относительную погрешность, равную сумме относительных погрешностей сомножителей, а абсолютная погрешность произведения должна вычисляться через относительную по общему правилу.
Из последнего правила можно, как частный случай произведения, получить зависимости для расчета погрешности при возведении приближенного числа в степень (равно как и вычислении корня из приближенного числа). Действительно, если вычисляется
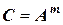
где 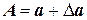
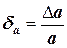
тогда 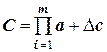
Учитывая, что 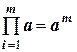
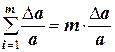
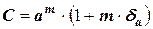
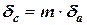
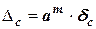
Задача 4. Определить, какое равенство записано точнее
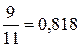
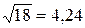
Решение. Находим значения равенств с большим числом десятичных знаков:
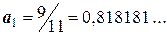
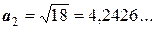
Затем вычисляем абсолютные погрешности:
Если увеличивать количество десятичных знаков после запятой, вычисляя а1 и а2 , соответственно также будут увеличиваться количество десятичных разрядов и у погрешности. Поэтому можно перейти к так называемым предельным абсолютным погрешностям:
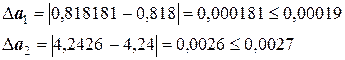
Абсолютные погрешности не позволяют провести сравнительный анализ двух вычислений на точность. С этой целью следует рассчитать относительные погрешности. Они будут равны:
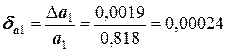
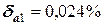
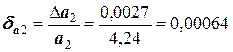
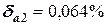
Очевидно, что первое вычисление выполнено с более высокой точностью, чем второе. Следовательно, только относительные погрешности позволяют сделать сравнительный анализ на достигнутую точность вычислений, причем на этот анализ не влияют ни абсолютные значения чисел, ни их размерность.
Задача 5. Вычислить и определить погрешности результата:
при следующих значениях величин:
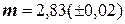
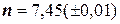
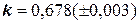
Решение. Находим результаты вычислений
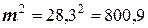
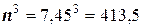
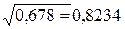
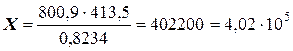
Рассчитываем относительные погрешности исходных чисел:
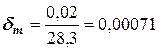
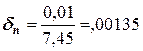
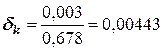
Рассчитаем погрешность результата:
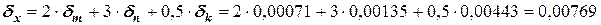
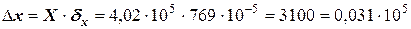
Ответ: 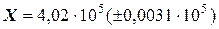
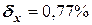
4) Вычислить и определить погрешности результата
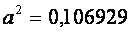
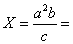
b =3,147
c=1,78
При умножении и делении чисел друг на друга их относительные погрешности складываются.
При возведении в степень приближенного числа его относительная погрешность умножается на показатель степени:
Получим, что d X = 2 d а + d b + d c =2*0,01529+0,00003+0,00056=0,03117=3,117%
Найдем абсолютную погрешность результата: 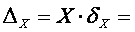
Ответ: Х=0,18905(±5,89*10 -3 ); d X =3,117%
2,265 просмотров всего, 3 просмотров сегодня