Система ограничений такой задачи состоит из неравенств от двух переменных:
и целевая функция имеет вид F = C 1 x + C2y, которую необходимо максимизировать.
Ответим на вопрос: какие пары чисел ( x; y ) являются решениями системы неравенств, т. е. удовлетворяют каждому из неравенств одновременно? Другими словами, что значит решить систему графически?
Предварительно необходимо понять, что является решением одного линейного неравенства с двумя неизвестными.
Решить линейное неравенство с двумя неизвестными – это значит определить все пары значений неизвестных, при которых неравенство выполняется.
Например, неравенству 3x – 5 y ≥ 42 удовлетворяют пары (x , y) : (100, 2); (3, –10) и т. д. Задача состоит в нахождении всех таких пар.
Рассмотрим два неравенства: ax + by≤ c, ax + by≥ c. Прямая ax + by = c делит плоскость на две полуплоскости так, что координаты точек одной из них удовлетворяют неравенству ax + by >c , а другой неравенству ax + +by
Пусть для определенности a< 0, b>0, c >0. Все точки с абсциссой x0, лежащие выше P (например, точка М), имеют yM>y0, а все точки, лежащие ниже точки P, с абсциссой x0, имеют yN c, образующие полуплоскость, а с другой стороны – точки, для которых ax + by
Знак неравенства в полуплоскости зависит от чисел a, b , c.
Отсюда вытекает следующий способ графического решения систем линейных неравенств от двух переменных. Для решения системы необходимо:
- Для каждого неравенства выписать уравнение, соответствующее данному неравенству.
- Построить прямые, являющиеся графиками функций, задаваемых уравнениями.
- Для каждой прямой определить полуплоскость, которая задается неравенством. Для этого взять произвольную точку, не лежащую на прямой, подставить ее координаты в неравенство. если неравенство верное, то полуплоскость, содержащая выбранную точку, и является решением исходного неравенства. Если неравенство неверное, то полуплоскость по другую сторону прямой является множеством решений данного неравенства.
- Чтобы решить систему неравенств, необходимо найти область пересечения всех полуплоскостей, являющихся решением каждого неравенства системы.
Эта область может оказаться пустой, тогда система неравенств не имеет решений, несовместна. В противном случае говорят, что система совместна.
Решений может быть конечное число и бесконечное множество. Область может представлять собой замкнутый многоугольник или же быть неограниченной.
Рассмотрим три соответствующих примера.
Пример 1. Решить графически систему:
x + y – 1 ≤ 0;
–2 x – 2y + 5 ≤ 0.
Решение:
- рассмотрим уравнения x+y–1=0 и –2x–2y+5=0 , соответствующие неравенствам;
- построим прямые, задающиеся этими уравнениями.
Рисунок 2
Определим полуплоскости, задаваемые неравенствами. Возьмем произвольную точку, пусть (0; 0). Рассмотрим x+ y– 1 0, подставим точку (0; 0): 0 + 0 – 1 ≤ 0. значит, в той полуплоскости, где лежит точка (0; 0), x + y – 1 ≤ 0, т.е. полуплоскость, лежащая ниже прямой, является решением первого неравенства. Подставив эту точку (0; 0), во второе, получим: –2 ∙ 0 – 2 ∙ 0 + 5 ≤ 0, т.е. в полуплоскости, где лежит точка (0; 0), –2x – 2y + 5≥ 0, а нас спрашивали, где –2x – 2y + 5 ≤ 0, следовательно, в другой полуплоскости – в той, что выше прямой.
Найдем пересечение этих двух полуплоскостей. Прямые параллельны, поэтому плоскости нигде не пересекаются, значит система данных неравенств решений не имеет, несовместна.
Пример 2. Найти графически решения системы неравенств:
Рисунок 3
1. Выпишем уравнения, соответствующие неравенствам, и построим прямые.
x + 2y– 2 = 0
| x | 2 | 0 |
| y | 0 | 1 |
y – x – 1 = 0
| x | 0 | 2 |
| y | 1 | 3 |
y + 2 = 0;
y = –2.
2. Выбрав точку (0; 0), определим знаки неравенств в полуплоскостях:
0 + 2 ∙ 0 – 2 ≤ 0, т.е. x + 2y– 2 ≤ 0 в полуплоскости ниже прямой;
0 – 0 – 1 ≤ 0, т.е. y –x– 1 ≤ 0 в полуплоскости ниже прямой;
0 + 2 =2 ≥ 0, т.е. y + 2 ≥ 0 в полуплоскости выше прямой.
3. Пересечением этих трех полуплоскостей будет являться область, являющаяся треугольником. Нетрудно найти вершины области, как точки пересечения соответствующих прямых
Рассмотрим еще один пример, в котором получившаяся область решения системы не ограничена.
Пример 3 . Решить графически систему
Выпишем уравнения, соответствующие неравенствам, и построим прямые.
Рисунок 4
x + y – 1 = 0
| x | 0 | 1 |
| y | 1 | 0 |
y – x – 1 = 0
| x | 0 | –1 |
| y | 1 | 0 |
Определим знаки в полуплоскостях. Выберем точку (0; 0):
0 – 0 – 1 ≤ 0, т.е. y – x – 1 ≤ 0 ниже прямой;
0 + 0 – 1 ≤ 0, т.е. x + y – 1 ≤ 0 ниже прямой.
Пересечением двух полуплоскостей является угол с вершиной в точке А(0;1). Эта неограниченная область является решением исходной системы неравенств.
- Решение онлайн
- Видеоинструкция
Заменив знаки неравенств на знаки равенств, получим систему граничных прямых:
Построим каждую из прямых на плоскости xOy по координатам двух точек.
Прямая l 1 проходит через точки ( 



полуплоскость, которая содержит точку (0;0), вместе с граничной прямой.
Аналогично, прямая l 2 проходит через точки ( 
0≤14 –верно, значит, решением неравенства является полуплоскость, содержащая точку (0;0), вместе с прямой l 2.
Прямая l 3 проходит через точки ( 
0≥38 – неверное числовое неравенство, значит, решением неравенства является полуплоскость, которая не содержит точку (0;0), вместе с граничной прямой.
Сделаем чертеж, на котором штриховкой укажем данные полуплоскости:
Заштрихованный треугольник АВС является областью решений системы линейных неравенств.
Прежде чем перейти к определению и решению неравенств давайте вспомним, какие знаки используют в математике для сравнения величин.
| Символ | Название | Тип знака |
|---|---|---|
| > | больше | строгий знак (число на границе не включается ) |
| строгий знак (число на границе не включается ) | ||
| ≥ | больше или равно | нестрогий знак (число на границе включается ) |
| ≤ | меньше или равно | нестрогий знак (число на границе включается ) |
Теперь мы можем разобраться, что называют линейным неравенством и чем неравенство отличается от уравнения.
В отличии от уравнения в неравенстве вместо знака равно « = » используют любой знак сравнения: « > », « », « ≤ » или « ≥ ».
Линейным неравенством называют неравенство, в котором неизвестное стоит только в первой степени.
Рассмотрим пример линейного неравенства.
Как решить линейное неравенство
Чтобы решить неравенство, нужно чтобы в левой части осталось только неизвестное в первой степени с коэффициентом « 1 ».
При решении линейных неравенств используют правило переноса и правило деления неравенства на число.
Правило переноса в неравенствах
Также как и в уравнениях, в неравенствах можно переносить любой член неравенства из левой части в правую и наоборот.
При переносе из левой части в правую (и наоборот) член неравенства меняет свой знак на противоположный .
Вернемся к нашему неравенству и используем правило переноса.
Для того, чтобы понять, что получается при решении неравенства, нам нужно вспомнить, понятие числовой оси.
Нарисуем числовую ось для неизвестного « x » и отметим на ней число « 14 ».
При нанесении числа на числовую ось соблюдаются следующие правила:
- если неравенство строгое, то число отмечается как «пустая» точка.
Это означает, что число не входит в область решения;
- если неравенство нестрогое, то число отмечается как «заполненная» точка.
Это означает, что число входит в область решения.
Заштрихуем на числовой оси по полученному ответу « x » все решения неравенства, то есть область слева от числа « 14 ».
Рисунок выше говорит о том, что любое число из заштрихованной области при подстановке в исходное неравенство « x − 6 » даст верный результат.
Возьмем, например число « 12 » из заштрихованной области и подставим его вместо « x » в исходное неравенство « x − 6 ».
Другими словами, можно утверждать, что любое число из заштрихованной области будет являться решением неравенства.
Решить неравенство — это значит найти множество чисел, которые при подстановке в исходное неравенство дают верный результат.
Решением неравенства называют множество чисел из заштрихованной области на числовой оси.
В нашем примере ответ « x » можно понимать так: любое число из заштрихованной области (то есть любое число меньшее « 14 ») будет являться решением неравенства « x − 6 ».
Правило умножения или деления неравенства на число
Рассмотрим другое неравенство.
Используем правило переноса и перенесём все числа без неизвестного, в правую часть.
Теперь нам нужно сделать так, чтобы при неизвестном « x » стоял коэффициент « 1 ». Для этого достаточно разделить и левую, и правую часть на число « 2 ».
При умножении или делении неравенства на число, на это число умножается (делится) и левая, и правая часть.
- Если неравенство умножается (делится) на положительное число, то
знак самого неравенства остаётся прежним . - Если неравенство умножается (делится) на отрицательное число, то
знак самого неравенства меняется на противоположный .
Разделим « 2x > 16 » на « 2 ». Так как « 2 » — положительное число, знак неравенства останется прежним.
Рассмотрим другое неравенство.
Разделим неравенство на « −3 ». Так как мы делим неравенство на отрицательное число, знак неравенства поменяется на противоположный.








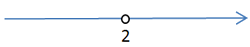 Это означает, что число не входит в область решения;
Это означает, что число не входит в область решения; Это означает, что число входит в область решения.
Это означает, что число входит в область решения.

это полное говно
это полное говно